Взаємний перетин поверхонь.

Лінія перетину поверхонь у загальному випадку представляє собою просторову криву. Але в різних випадках ця просторова крива може містити частини плоских кривих і ламані лінії, якщо у взаємному перетині, приміром, беруть участь гранні і криві поверхні. У деяких випадках крива лінія перетину може розпадатися на частини.

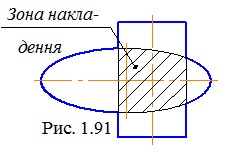На кресленні проекції просторової лінії перетину будують звичайно, за допомогою окремих точок, знаходячи спочатку опорні, які дозволяють бачити характер лінії перерізу, (найвища, найнижча, перетин контурних ліній або ребер і т.ін.), а потім довільні точки, що уточнюють положення цієї лінії. Важливим є те, що проекції лінії перетину завжди розташовуються в межах зони накладення однойменних проекцій пересічних поверхонь (рис. 1.91).

Виділимо кілька випадків розташування поверхонь стосовно площин проекцій.

1.Обидві поверхні займають проекціююче положення. На рис. 1.92 показана побудова лінії перетину двох циліндричних поверхонь, одна з яких горизонтально-проекціююча, а друга фронтально-проекціююча. У техніці це відповідає типовим випадкам "урізання" (з'єднання) двох трубопроводів, осі яких розташовуються під прямим кутом одна до одної. Горизонтальна й фронтальна проекції лінії перетину збігаються зі слідами-проекціями поверхонь, тобто з окружностями, але займають їх не повністю, а тільки в зоні накладення проекцій.

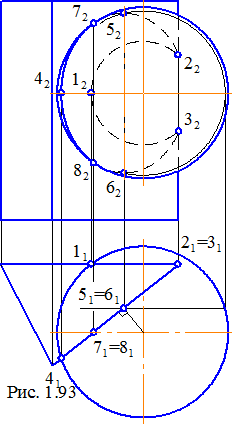
Відзначимо кілька особливих точок, виділимо їхні проекції і побудуємо їх на виді ліворуч, де проекція лінії перерізу не збігається з якими-небудь іншими лініями. Точки 1 і 2 лежать на крайній лівій твірній проекціюючої поверхні, точки 7, 8 і 9, 10 – на верхній і нижній твірній тієї ж поверхні, 3, 5 і 4, 6 – на передній і задній твірній горизонтально-проекціюючої поверхні, і останні особливі точки – 11 і 12 – на правій крайній твірній цієї поверхні. Отримані проекції точок на виді зліва з'єднаємо плавною лінією з урахуванням її видимості.

2.Одна з поверхонь займає проекціююче положення, а друга ні. Це найпоширеніший тип завдань, що зустрічаються в інженерній практиці.

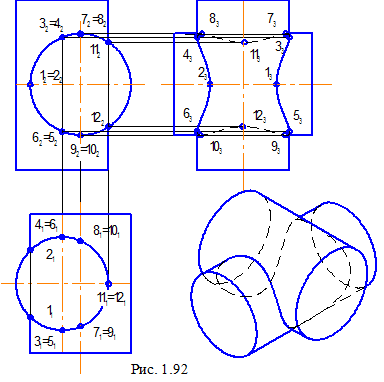
На рис. 1.93 показана побудова лінії перетину призматичної і сферичної поверхонь. По виду поверхонь можна заздалегідь представити характер лінії перетину: вона складається із двох плоских частин – окружностей, які утворюються в результаті перетину двох граней призматичної поверхні зі сферою. З'єднуються вони між собою у двох точках 2 і 3 перетину ребра призматичної поверхні зі сферою.

Призматична поверхня займає горизонтально-проекціююче положення, тому, на виді зверху проекція лінії перетину збігається з проекціями граней у границях зони накладення зображень, а на виді спереду – частиною окружності (задня грань займає фронтальне положення) і частиною еліпса.

Для побудови фронтальної проекції окружності, на П₁ необхідно відзначити крайню точку 1, перетину задньої грані з екватором сфери, замірити радіус окружності і провести дугу, обмеживши її точками 2 і 3 на правій границі зони накладення проекцій. Для побудови еліпса, крім згаданих точок 2 і 3, використані особливі точки: 4 – крайня ліва точка перетину, яка розташована на екваторі, точки 7 і 8, що лежать на головному меридіані сфери і точки 5 і 6, що визначають положення й величину великої осі еліпса.

Знаходження останніх двох точок вимагає побудов: через їхні горизонтальні проекції проведена окружність, яка паралельна площині П₂. Фронтальні проекції точок визначають на перетині цієї окружності з вертикальною лінією зв'язку. Додаткові точки для збільшення точності побудов, при необхідності, можна знайти таким само способом.

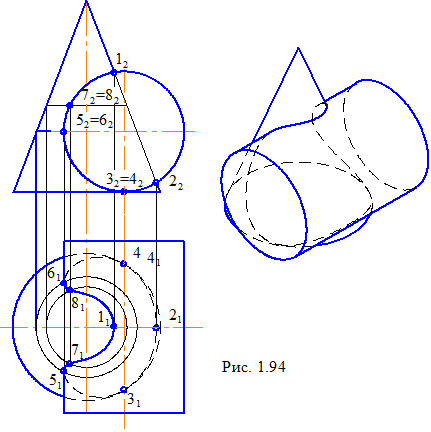
Розглянемо ще один приклад. На рис. 1.94 задані конічна й циліндрична поверхні обертання, осі яких – мимобіжні і взаємно перпендикулярні. Поверхня циліндра проекціююча, отже, на фронтальній площині проекцій лінія перерізу буде збігатися зі слідом-проекцією цієї поверхні.

Для побудови горизонтальної проекції лінії перетину виділимо особливі точки, що належать до цієї лінії: точки 1 і 2 лежать на крайній правій твірній конуса, 3 і 4 – на лінії, що обмежує конічну поверхню. Положення цих ліній на горизонтальній площині проекцій відомо, тому побудова перерахованих точок зводиться до проведення вертикальних ліній зв'язку. Для знаходження точок 5 і 6, що лежать на лівій крайній твірній циліндричної поверхні, через їхні фронтальні проекції на конічній поверхні проводять окружність, визначають її радіус і будують на площині П₁. Точки будуть перебувати на перетині вертикальної лінії зв'язку з цією окружністю. Будь-які проміжні точки, включаючи показані 7 і 8, одержують у такий само спосіб.

Розглянемо більше складний випадок перетину, коли обидві поверхні (конічна й сферична) займають загальне положення (рис. 1.95).

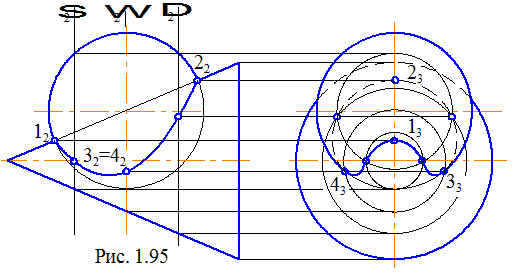Аналізуючи взаємне положення поверхонь, дійдемо висновку, що оскільки центр сфери розташовується в площині симетрії конуса і ця площина розташовується паралельно площині проекцій П₂, лінія взаємного перетину поверхонь на горизонтальній площині проекцій буде так само мати вісь симетрії, а на фронтальній – її видима і не видима частини будуть збігатися. Не важко знайти крайні ліву і праву точки лінії перетину (точки 1 і 2), тому що головний меридіан сфери і крайня твірна конусу лежать в одній фронтальній площині, й, отже, перетинаються між собою.

Проміжні точки лінії перерізу можна знайти, вводячи допоміжні січні площини особливого положення. У якості таких прийняті профільні площини Σ, Ω і Δ, тому що наведені на кресленні поверхні вони перетинають по простих лініях. Кожна з узятих допоміжних площин перетинає конус і сферу по окружностях. Ці окружності у свою чергу перетинаючись між собою, дають дві точки, що належать лінії взаємного перетину поверхонь. Площини Σ, і Δ узяті на однаковій відстані від центра сферичної поверхні, що дозво 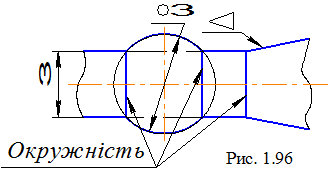лило скоротити кількість ліній побудови.

Слід зазначити випадки побудови ліній перетину співвісних поверхонь обертання. Таке завдання дуже часто зустрічається на практиці при конструюванні внутрішніх і зовнішніх форм деталей. Співвісними поверхнями називають поверхні, що мають загальну вісь обертання. На рис. 1.96 показаний перетин трьох співвісних поверхонь: циліндра, конуса й сфери. Їхньою загальною віссю є профільно-проекціююча пряма.

Співвісні поверхні обертання завжди перетинаються по окружностях, площини яких перпендикулярні осі обертання. Таких окружностей буде стільки, скільки існує точок перетину нарисових ліній поверхонь.

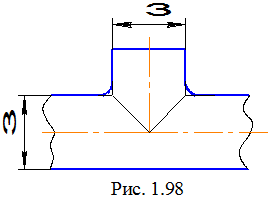
У цьому випадку можна скористатися теоремою, що (трохи спрощуючи) можна викласти в такий спосіб: якщо дві поверхні обертання можна описати навколо однієї сфери, то вони перетинаються між собою по плоских кривих. За певних умов розташування поверхонь (наприклад, якщо їхні осі паралельні площині проекцій), ці плоскі криві на кресленні зображуються у відрізки прямих ліній, що істотно полегшує побудови (рис. 1.97).

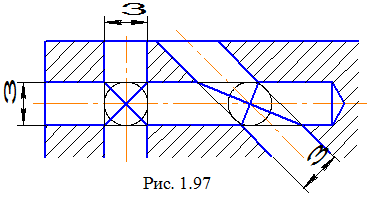
У конструкціях деталей при перетині поверхонь використовують поверхню, (найчастіше торову), що здійснює плавний перехід від однієї поверхні до іншої (рис.1. 98). У цих випадках, замість лінії перетину основних поверхонь, проводять умовну лінію, що називається лінією переходу. Вона виконується тонкою суцільною лінією і закінчується в точках перетину нарисових ліній основних поверхонь.

◊ Як будують лінію перетину двох поверхонь, якщо одна з них займає проекціююче положення?

◊ По яких лініях перетинаються співвісні поверхні обертання?