Пряма перпендикулярна до площини, якщо вона перпендикулярна до двох прямих цієї площини, що перетинаються.

Спочатку розглянемо часткові випадки, коли площина паралельна або перпендикулярна до площини проекцій.

Випадок 1. Якщо площина паралельна площині проекцій, то пряма, яка перпендикулярна до неї, буде проецюючою. Одна з її проекцій буде перпендикулярною до сліду проекції площини.

Наприклад, задано площину S ІІ П₁(рис. 4.16-а) і точку А(А₁,А₂). Необхідно через точку А провести пряму ί ^ S.

Оскільки S ІІ П₁, а ί ^ S, то ί ^ П₁. А Î ί : ί₁º А₁, ί₂^ S₂.

а) б)

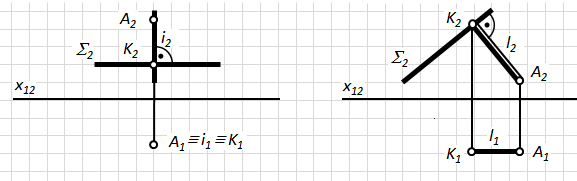
Рис.4.16.

Випадок 2. Якщо площина займає проецююче положення, то пряма лінія, яка перпендикулярна до площини, буде прямою рівня.

Наприклад, задано площину S ^ П₂(рис. 4.16-б) і точку А(А₁,А₂). Необхідно через точку А провести пряму l ^ S.

Оскільки площина S ^ П₂, а l ^ S, то пряма l ІІ П₂Þ l₁ ІІ X₁₂, l₂ ^ S₂.

Випадок.3. Якщо площина S займає загальне положення, то і перпендикуляр до цієї площини теж буде займати загальне положення.

Наприклад, задано площину S в системі площин проекцій П₁П₂(рис. 4.17-а). Пряма n ^ S. А – основа перпендикуляра на площині S. Якщо провести через точку А у площині S фронталь f і горизонталь h, то ці прямі утворять з прямою n прямі кути, як і будь-які інші прямі, що належать площині S, оскільки з геометрії відомо, що пряма, перпендикулярна до площини, перетинається або схрещується під прямим кутом з будь-якою прямою, проведеною на цій площині.

Але на комплексному кресленні перпендикулярність зберігається не з кожною прямою. Саме тому ми виділяємо фронталь і горизонталь.

Через те, що h ІІ П₁, прямий кут, утворений нею з прямою n ^ S спроецюється на П₁без спотворення на основі теореми про проеціювання прямого кута. З тієї ж причини кут, утворений f з прямою n ^ S, спроецюється на П₂також без спотворення.

Таким чином, для побудови проекцій перпендикуляра до площини необхідно мати лінії рівня чи сліди площини (рис. 4.17-б): S – площина загального положення, А Î S , n ^ S , A Î n, h і f Ì S, h ІІ h₁⁰: f ІІ f₂⁰ : n₁ ^ h₁⁰ : n₂ ^ f₂⁰.

а) б)

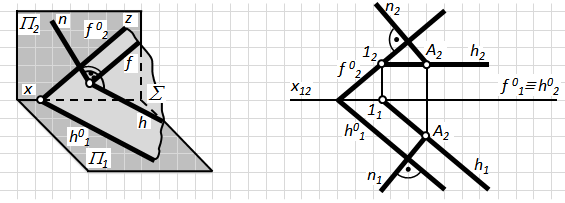
Рис.4.17.

Висновок. Для того, щоб пряма у просторі була перпендикулярна до площини, необхідно і достатньо, щоб на комплексному кресленні горизонтальна проекція прямої була перпендикулярна до горизонтальної проекції горизонталі площини, а фронтальна проекція прямої перпендикулярна до фронтальної проекції фронталі площини (або необхідно і достатньо, щоб проекції цієї прямої були перпендикулярні до однойменних слідів площини): n₁ ^ h₁, n₂ ^ f₂Û n ^ S(f, h).

Можна провести перпендикуляр до площини з будь-якої точки, а потім розв'язувати задачу про знаходження точки перетину прямої з площиною. Розвиваючи цю думку, приходимо до задачі на визначення відстані від точки до площини.

Задача 1. Визначити відстань від точки А(A₁, A₂) до площини S (c ІІ d) (рис. 4.18-а).

Відстань від точки до площини вимірюється довжиною відрізка перпендикуляра, опущеного з точки на площину : n ^ S; A Î n .

1) Проводимо лінії рівня площини h і f.

2) Проводимо проекції перпендикуляра з точки А до площини S:

n₁ ^ h₁; n₂ ^ f₂. Зауважимо, що пряма n схрещується з f і h під прямими кутами, а тому основи перпендикуляра на площині ми не маємо.

3) Знаходимо точку K перетину прямої n з площиною S: K = n Ç S.

4) Визначаємо натуральну величину відрізка перпендикуляра АК способом прямокутного трикутника.

Можна розв'язати зворотну задачу, тобто побудувати площину, перпендикулярну до заданої прямої.

а) б)

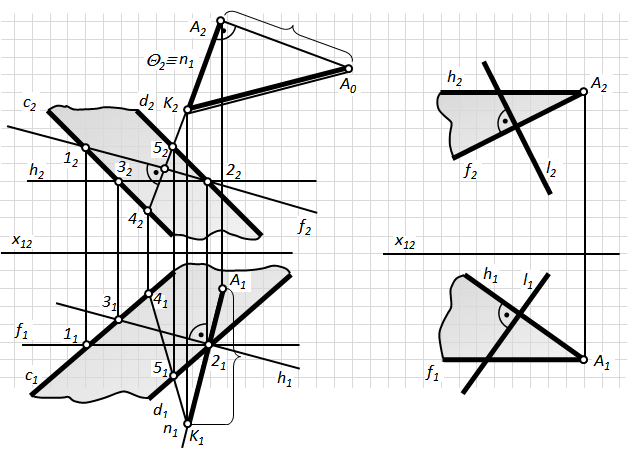
Рис.4.18. Знаходження відстані від прямої до площини

Задача 2. Через точку А(A₁, A₂) провести площину Q, яка перпенди-кулярна до прямої l. Пряма l – загального положення

Площина буде перпендикулярна до прямої, якщо дві перетині прямі цієї площини будуть перпендикулярні до заданої прямої. А тому проведення через точку А площини Q, перпендикулярної до прямої l, виконується шляхом побудови фронталі і горизонталі, які схрещуються під прямими кутами із заданою прямою: А Î Q; Q (h Ç f): h₁ ^ l₁; f₂ ^ l₂(рис. 4.18-б).

Дві площини взаємно перпендикулярні, якщо одна з них проходить через перпендикуляр до другої.Тому достатньо, щоб серед елементів, які задають площину Q, яка перпендикулярна площині S, був перпендикуляр до площини S (DABC).

Задача 1.Через точку М провести площину Q, яка перпендикулярна до заданої площини S (рис. 4.19).

Щоб провести через точку М площину, перпендикулярну до площини Q, треба спочатку з точки М опустити перпендикуляр на цю площину.

1) Проводимо h i f Ì S.

2) Проводимо проекції перпендикуляра l, опущеного з точки М на площину S: l₁^ h₁; l₂^ f₂.

3) Будуємо площину Q (l Ç m). Пряму m Þ m₁, m₂проводимо довільно, оскільки площин, які проходять через пряму l і перпендикулярних до площини S, безліч, а тому довільною прямою m визначена одна з можливих.

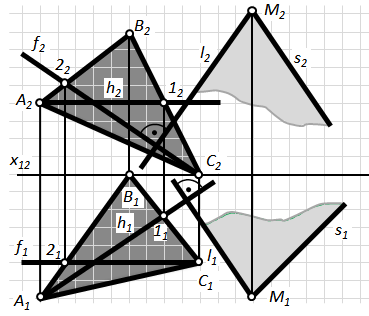
Рис.4.19. Перпендикулярність двох площин