КОМПЛЕКСНОГО КРЕСЛЕННЯ

1.Трудомісткість і, як наслідок, точність графічного розв'язання задач часто залежать не тільки від складності задач, але і від того, яке положення займають геометричні фігури, що входять в умову задачі, по відношенню до площин проекцій.

Фігура, яка проецюється, як відомо, може займати по відношенню до площин проекцій чи довільне чи особливе положення. У першому випадку, як правило, отримуємо проекції, незручні для розв'язання задач. В той же час розв'язання задач значно спрощується, коли ми маємо справу з особливим розміщенням геометричних фігур відносно площин проекцій.

Найбільш вигідними особливими положеннями фігури, при яких можуть бути одержані проекції, зручні для розв'язання задач, слід вважати:

а) положення, паралельне площині проекцій;

б) положення, перпендикулярне до площини проекцій.

Так, наприклад, при розміщенні фігури паралельно будь-якій площині проекцій вона проецюється на цю площину в натуральну величину; за проекцією прямої особливого положення можна визначити довжину її відрізків, величину кутів нахилу до площин проекцій; відстань від точки до прямої проецюється на площину проекцій без спотворення, якщо дана пряма перпендикулярна до площини проекцій і т.п.

У зв’язку з цим є потреба в прийомах, які б дали змогу перевести задану фігуру із загального положення в особливе по відношенню до площин проекцій.

Цього можна досягти двома шляхами:

1) вибором нової площини проекцій, по відношенню до якої фігура, що проецюється, не змінює свого положення у просторі, займе особливе положення (спосіб заміни площин проекцій);

2) переміщенням у просторі фігури, яка проецюється так, щоб вона зайняла часткове положення відносно площин проекцій, які при цьому не змінюють свого положення у просторі (способи обертання, спосіб плоско-паралельного переміщення).

2. Зміна взаємного положення фігури, яка проецюється, і площин проекцій досягається шляхом переходу від заданих площин проекцій до нових.

Нова площина проекцій вибирається перпендикулярною до однієї з старих площин проекцій.

Геометричні фігури, які проецюються, при цьому не змінюють свого положення у просторі.

Вибираючи положення нової площини проекцій, слід керуватися тим, щоб по відношенню до нової площини проекцій фігури, яка проецюється, займала особливе (часткове) положення, яке забезпечує одержання проекцій, найбільш зручних для розв'язання поставленої задачі.

Якщо заміна однієї площини проекцій не забезпечує потрібного вигляду допоміжної проекції, виконують подальшу заміну.

При цьому перехід від заданої системи площин проекцій Х₁₂ 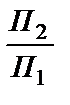до нової Х₄₅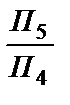 може бути здійснений за однією з наступних схем:

Х₁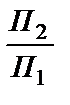₂ ® Х₄₂ ®Х₄₅ ;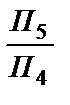

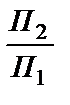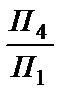Х₁₂ ® Х₁₄ ®Х₅₄ .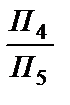

Наведені схеми показують, що водночас ми можемо замінювати тільки одну площину проекцій. Друга площина при цьому залишається незмінною.Наявність однієї площини проекцій, яка не змінює свого положення, дозволяє використовувати її як сполучну ланку між старими (вихідними) проекціями і новими.

В систему площин П₁і П₂(рис. 5.1-а) вводиться додаткова площина П₄. Площину П₄вибираємо так, щоб вона була паралельна відрізку АВ і перпендикулярна площині П₁. П₄ ІІ АВ і П₄ ^ П₁.

Утворена нова система площин 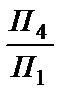. Ці площини між собою перетинаються по новій осі Х₁₄. Ця вісь паралельна проекції відрізка А₁В₁. Оскільки П₄// АВ, то проекція АВ на П₄є натуральною величиною, а відрізок АВ в системі площин проекцій 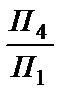є фронталлю.

а) б)

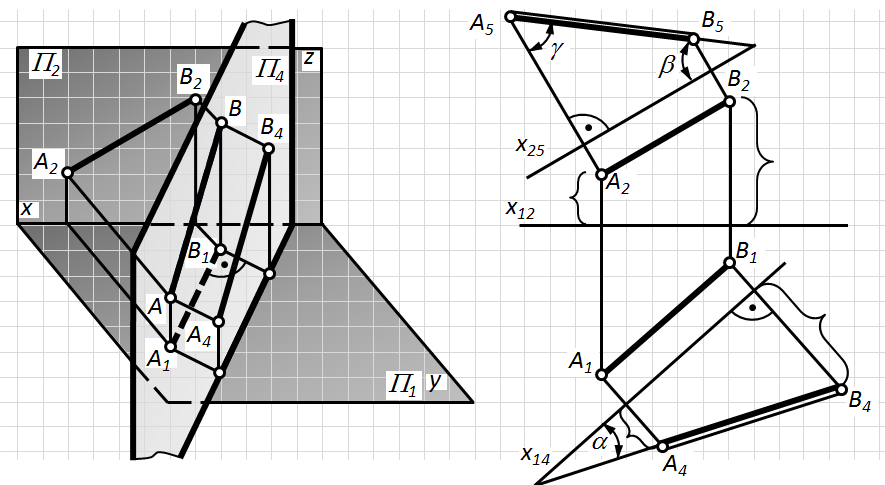
Рис. 5.1. Спосіб заміни площин проекцій

При заміні однієї з площин проекцій необхідно керуватись такими правилами:

1. Залежно від умови задачі вибираємо нову площину проекцій. Лінія перетину нової площини з незмінною площиною проекцій є новою віссю проекцій (Х₁₄).

2. Через незмінну проекцію точки проводимо нову лінію зв’язку перпендикулярну до нової осі проекцій.

3. На новій лінії зв’язку від нової осі проекцій відкладаємо координату проекції, яка замінюється (відстань від точки до незмінної площини проекцій).

Примітка:При відсутності на епюрі Монжа осі проекцій координати точок слід відраховувати від буд-якої горизонтальної лінії відліку.

Приклад 1.Перетворити пряму загального положення в проецюючу пряму і визначити кути нахилу її до площин проекцій (рис. 5.1-б).

1) П₄ ІІ АВ: П₄ ^ П₂; П₄Ç П₂= Х₂₄: Х₂₄ ІІ А₂В₂. В системі 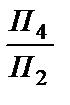пряма АВ є горизонталлю: В₄А₄– натуральна величина відрізка АВ, a і b – натуральна величина кутів його нахилу до відповідних площин проекцій.

П₅ ^ АВ: П₅ ^ П₄; П₄ Ç П₅= Х₄₅: Х₄₅ ^ А₄В₄; в системі 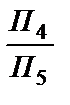пряма АВ є проецюючою.

2) П₆ ІІ АВ: П₆ ^ П₁; П₆Ç П₁= Х₁₆: Х₁₆ ІІ А₁В₁; в системі пряма АВ є фронталлю. А₆В₆– натуральна величина відрізка АВ, a і g – натуральна величина кутів його нахилу до відповідних площин проекцій.

Приклад 2.Визначити натуральну величину DАВС і кути a і b його нахилу до П₁і П₂. DАВС - площина загального положення (рис. 5.2).

При розв’язуванні цієї задачі необхідно виконати подвійне перетворення (подвійну заміну площин проекцій): спочатку перетворити площину загального положення в проецюючу площину, а потім проецюючу площину в площину рівня.

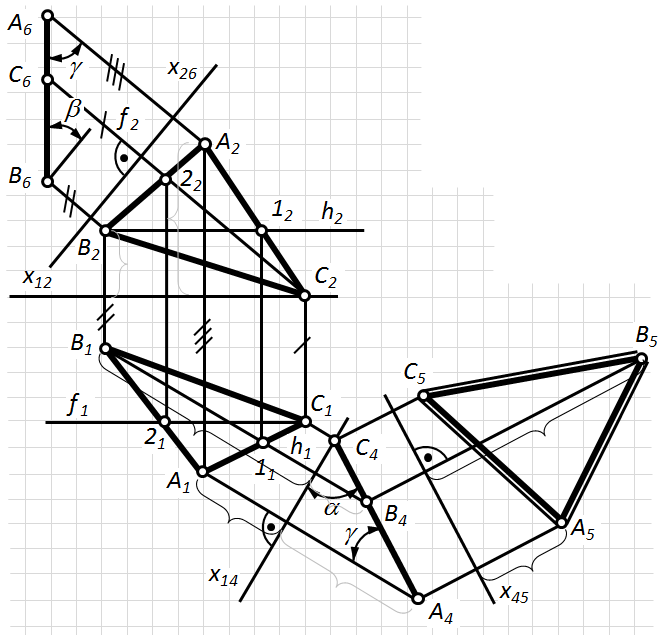1)Проводимо лінії рівня площини – h і f.

2) Вибираємо П₄ ^ h; П₄ ^ П₁, П₄ Ç П₁= Х₁₄; Х₁₄ ^ h₁.

В системі горизонталь стане проецюючою

прямою, а площина DАВС – проецюючою

площиною. a і g – натуральна величина

кутів нахилу площини DАВС до

відповідних площин проекцій.

3) П₅ ІІ D АВС; П₅ ^ П₄,

П₅ Ç П₄ = Х₄₅; Х₄₅ ІІ А₄В₄С₄;

D А₅В₅С₅ – натур. вел. DАВС.

Рис. 5.2. Визначення натуральних величин відрізків та кутів нахилу способом заміни площин проекцій

4) П₆ ^ DАВС : П₆ ^ f; П₆ ^ П₂, П₆ Ç П₂= Х₂₆; Х₂₆ ^ f₂: b і g - натуральна величина кутів нахилу площини DАВС до відповідних площин проекцій.

3. На відміну від способу заміни площин проекцій, де задана фігура залишалась нерухомою, а площини проекцій змінювали своє положення, можна досягти того ж самого результату зворотним шляхом: залишаючи площини проекцій нерухомими, переміщувати фігуру у просторі як тверду систему до бажаного положення.

Плоско-паралельним переміщенням фігури у просторі називається таке переміщення, при якому усі точки фігури переміщуються у площинах, паралельних між собою і паралельних до площини проекцій.

Так, у плоско-паралельному переміщенні відносно П₁ усі точки фігури переміщуються у горизонтальних площинах рівня.

Теорема.Якщо фігура здійснює плоско-паралельне переміщення відносно П₁, то фронтальні проекції її точок будуть рухатися по прямих, перпендикулярних до ліній зв'язку. У цей час горизонтальна проекція фігури рухається по площині проекцій, залишаючись рівною самій собі.

У випадку плоско-паралельного переміщення фігури відносно П₂горизонтальні проекції її точок рухаються по прямих, перпендикулярних до ліній зв'язку, а фронтальна проекція фігури переміщується по площині проекцій, залишаючись рівною самій собі.

Приклад 1. Перетворити пряму загального положення в проецюючу пряму (рис. 5.3).

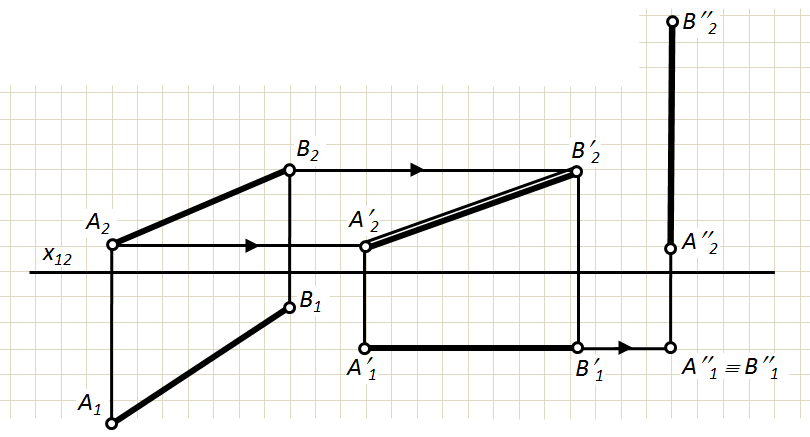
Рис. 5.3. Плоско-паралельне переміщення прямої

Спочатку перетворюємо комплексне креслення так, щоб відрізок АВ став паралельним до П₂, а потім так, щоб став перпендикулярним до П₁.

ôА₁В₁ô = ôА₁В₁ô, А₁¢В₁¢ ІІ Х₁₄. ôА₂¢В₂¢ô = ôА₂¢В₂¢ô, А₂В₂ ^ Х₁₂.

Приклад 2. Визначити натуральну величину DАВС. DАВС – площина загального положення (рис. 5.4).

Перетворення проводимо в два етапи:

1) Перетворюємо площину загального положення в проецюючу. Для цього в площині проводимо лінію рівня – h або f. Розміщуємо ту проекцію площини, в якій лінія рівня є натуральною величиною так, щоб натуральна величина лінії рівня стала перпендикулярною до осі проекцій Х₁₂. При цьому лінія рівня стане проецюючою прямою і на другу площину проекцій спроецюється в точку. Площина при цьому стане проецюючою відносно цієї ж площини проекцій..

2) Перетворюємо проецюючу площину в площину рівня. Для цього ту проекцію площини, яка являє собою пряму лінію розташовуємо паралельно осі Х₁₂. Інша проекція буде являти собою натуральну величину DАВС .

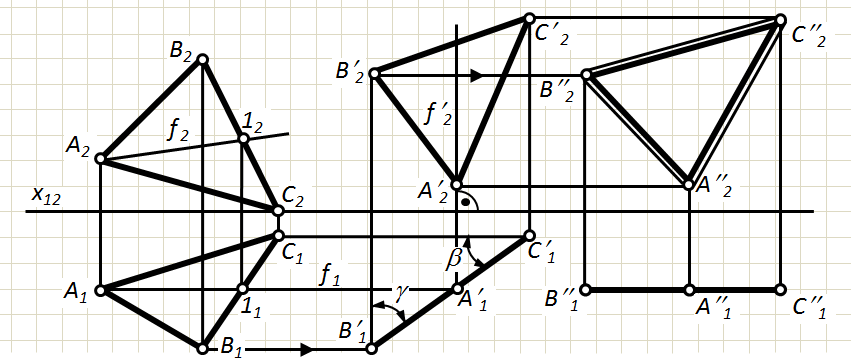
Рис. 5.4. Плоско-паралельне переміщення площини