ПОВЕРХНІ.

1. Многогранником називається тіло, яке обмежене плоскими многокутниками. Елементами многогранника є: площини (грані), ребра (лінії перетину двох граней), вершини (спільні точки декількох граней).

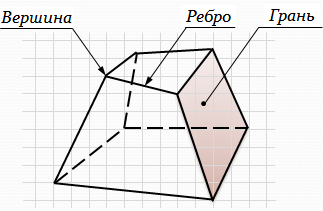Рис.6.1.

У правильних опуклих многогранників усі ребра, грані, плоскі двогранні та просторові кути дорівнюють один одному.

Різновидності правильних многогранників:

1) Тетраедр (чотиригранник) – грані рівні трикутники;

2) Октаедр (восьмигранник) – грані рівні трикутники;

3) Ікосаедр (двадцятигранник) – грані рівні трикутники;

4) Гексаедр (шестигранник) – грані квадрати;

5) Додекаедр (дванадцятигранник) – грані правильні п’ятикутники.

Навколо всіх правильних многоранників можна описати сферу.

Пірамідою (рис.6.2-б) називається многогранник у якого всі бічні ребра перетинаються в одній точці.

Призмою(рис.6.2.-а) називається многогранник у якого всі бічні ребра паралельні між собою. Основами призми є рівні многокутники. Якщо основи призми перпендикулярні бічним ребрам, то призма називається прямою. Якщо цієї умови немає – призма похила. Побудова проекцій многогранника зводиться до побудови його сітки.

а) б)

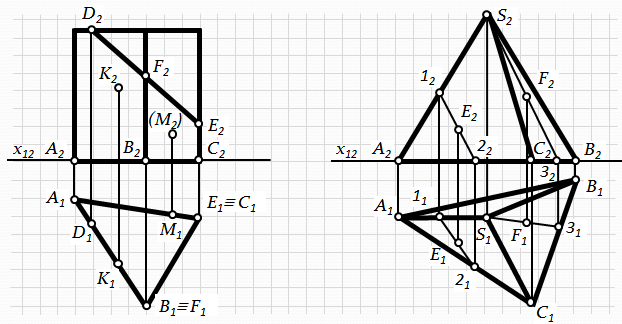
Рис.6.2. Побудова проекцій многогранників

Комплексне креслення призм, пірамід і інших многогранників краще виконувати з тих площин проекцій, на які їх основи проецюються в натуральну величину.

При розв’язанні різних задач часто необхідно визначити на поверхні многогранника точку чи відрізок прямої. Ця задача полегшується, якщо точка чи відрізок знаходяться у проецюючих гранях. Наприклад: бічні грані прямої призми (рис. 6.2-а). У випадку загального положення граней виконують такі ж самі побудови, як при визначенні точки чи відрізка прямої, що належить площині загального положення.

Так, якщо задані фронтальні проекції K₂, M₂точок, що лежать на поверхні призми (рис. 6.2-а), то горизонтальні проекції цих точок визначаються просто. Бічні грані призми є горизонтально-проецюючими, тому горизонтальні проекції всіх точок, що лежать у цих гранях збігаються зі слідами-проекціями відповідних граней.

Якщо точки E і F лежать на бічних гранях піраміди (рис. 6.2-б), то для визначення відсутніх проекцій точок, необхідно в гранях через ці точки провести довільні прямі, визначити положення проекцій цих прямих на проекціях граней многогранника, а потім визначити положення проекцій точок E і F на проекціях відповідних прямих, яким вони належать.

2.При перерізі многогранника площиною утворюється плоска фігура, що називається перерізом. Перерізом многогранника є многокутник вершинами якого служать точки перетину ребер многогранника з січною площиною, а сторонами є лінії перетину цієї площини з гранями многогранника.

Розрізняють два способи побудови плоского перерізу многогранника:

1) знаходження вершин многокутника перерізу (спосіб ребер);

2) знаходження сторін многокутника перерізу (спосіб граней).

У першому випадку побудова зводиться до багатократного розв'язання задачі на знаходження точки перетину прямої з площиною (перша позиційна задача), у другому випадку – на знаходження лінії перетину двох площин (друга позиційна задача). Можлива комбінація в використанні цих двох способів.

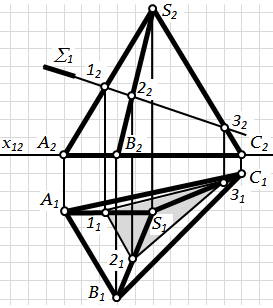Рис.6.3. Переріз многогранника проецюючою площиною

Розв'язання задачі на визначення перерізу многогранника площиною значно спрощується, якщо січна площина займає проецююче положення. У цьому випадку одна з проекцій перерізу – відрізок прямої – належить сліду-проекції січної площини.

Визначення другої проекції лінії перерізу зводиться до розв'язання раніше розглянутої задачі на побудову відсутньої проекції точки, що належить многограннику, якщо відома хоча б одна її проекція.

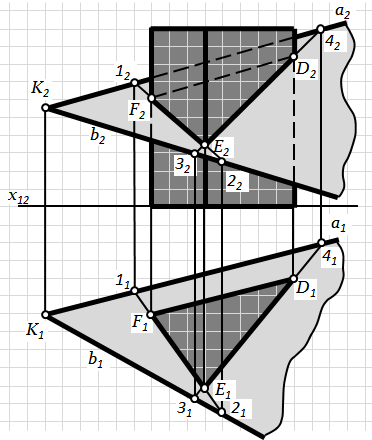Рис.6.4. Переріз многогранника площиною

На відміну від попередньої задачі переріз призми площи-ною S на площини проекцій П₁і П₂не проецюється у вигляді прямої лінії.

Але, оскільки бічна поверхня призми є горизонтально-проецюю-ча (три бічні грані є площинами, перпендику-лярними до П₁), то горизонтальна проекція перерізу призми площи-ною S збігається з горизонтальною проекці-єю призми. Внаслідок цього горизонтальні проекції вершин перерізу збігаються з горизонтальними проекціями ребер призми, а горизонтальні проекції сторін перерізу – з горизонтальними проекціями граней призми.

Задачу розв'язуємо способом граней, двічі розв'язуючи задачу про перетин двох площин, одна з яких є горизонтально-проецюючою.

Приклад 3. Побудувати проекції перерізу трикутної призми площиною S(m Ç n) - загального положення (рис. 6.5).

Розв'язання задачі ускладнюється тим, що на П₁і П₂переріз не проецюється у вигляді відрізка прямої, а бічна поверхня призми не є проецюючою – бічні грані займають загальне положення.

В заданому випадку необхідно використати спосіб ребер: послідовно побудувати точки перетину бічних ребер з площиною загального положення. Для цього через бічні ребра проводимо допоміжні площини (в даному випадку – горизонтально-проецюючі Q, L, W) – тричі розв'язуємо задачу про перетин прямої з площиною.

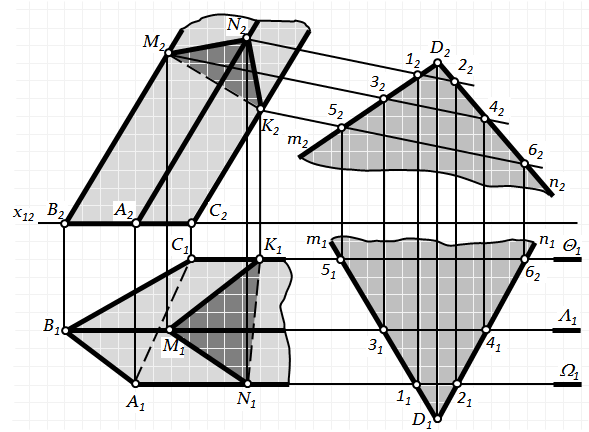
Рис.6.5. Переріз трикутної призми площиною

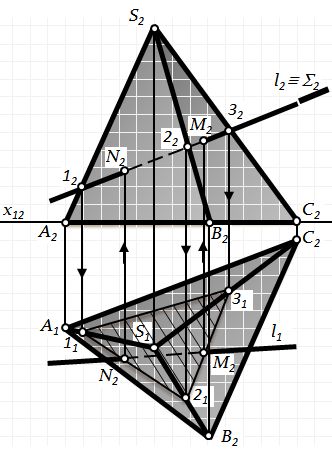Рис.6.6. Побудова точки перетину прямої зповерхнею піраміди

Приклад 1.Визначити точки перетину прямої l з поверхнею піраміди.

1. Через пряму l проводимо фронт.-проецюючу площину S – l₂ º S₂.

2. Будуємо проекції перерізу піраміди площиною: 1₂,2₂,3₂®1₁,2₁,3₁.

3. Визначаємо точки перетину прямої l з побудованим перерізом – точки M і N (M₁,N₁® M₂, N₂).

4. Визначаємо видимість прямої на П₁і П₂.