Якщо проекція сліду площини не перетинається з проекцією основи поверхні, то пряма не перетинається з поверхнею.

4. Обрисами багатьох інженерних конструкцій і споруд, деталей машин і механізмів є криві лінії. Кривими лініями складаються каркаси і сітки поверхонь.

Будь-яка крива лінія може бути отримана:

1) рухом точки у просторі (рис. 6.8-а);

2) перетином кривих поверхонь площиною (рис. 6.8-б);

3) взаємним перетином двох поверхонь, з яких хоча б одна крива (рис. 6.8-в).

а) б) в)

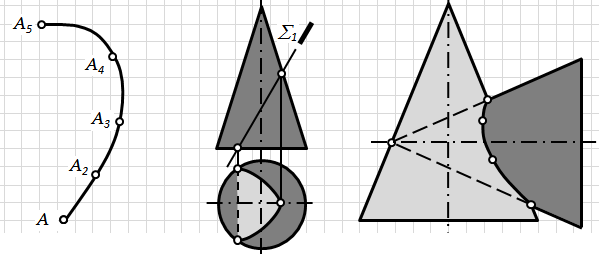
Рис.6.8. Способи утворення кривих ліній

5. Плоскими називаються криві лінії, всі точки яких лежать в одній площині.

Ознакою плоскої кривої на епюрі є належність проекцій всіх точок кривої однойменним проекціях прямих, які належать площині (рис. 6.9).

Рис.6.9. Плоскі криві лінії

Тобто, за двома ортогональними проекціями кривої неможливо одразу відповісти на запитання, плоскій чи просторовій кривій відповідають задані проекції. Необхідно з'ясувати, чи належать усі точки кривої одній площині. Якщо належать, крива – плоска, якщо не належать – просторова.

Просторовими називаються криві лінії, всі точки яких не належать одній площині (рис 6.10-а).

а) б)

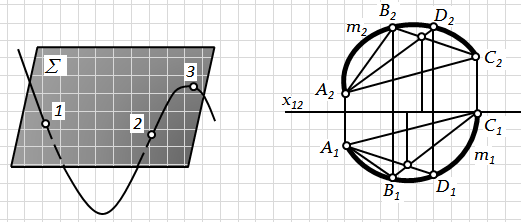
Рис.6.10. Просторові криві лінії

Щоб визначити, плоска чи просторова крива лінія m(m₁, m₂) задана на епюрі (рис. 6.10-б), необхідно:

1) позначити на кривій m три довільні точки А, В, С, які визначають собою площину;

2) взяти на кривій m четверту довільну точку D і перевірити, чи належить вона цій площині.

Виявилось, що точка D площині АВС не належить.

Крива лінія m(m₁, m₂) просторова.

Алгебраїчний порядок кривої визначає степінь її рівняння.

Геометричний порядок плоскої кривої дорівнює найбільшій можливій кількості точок перетину її з прямою лінією, а порядок просторової кривої – кількості точок перетину її з площиною загального положення.

Основні властивості проекцій плоских кривих:

1) порядок плоскої алгебраїчної кривої при паралельному проеціюванні не змінюється;

2) нескінченно віддалені точки кривої проецюються в нескінченно віддалені точки її проекції;

3) дотична до кривої проецюється в дотичну до її проекції;

4) число точок перетину плоских кривих зберігається при проеціюванні;

5) проекції точок перетину знаходяться на спільних лініях зв’язку.

Коло є найбільш поширеною в техніці плоскою кривою. У загальному випадку коло проецюється в еліпс, велика і мала осі якого є проекціями взаємно перпендикулярних діаметрів кола.

Проекційні властивості просторових кривих ліній такі ж самі як і плоских кривих. Але є і деякі відмінності. Так, наприклад, просторова крива лінія проецюється тільки в плоску криву. Зображення точок на проекціях кривих ліній може не відповідати положенню самих точок.

З усіх просторових кривих ліній, що використовуються в техніці, найбільш розповсюджені гвинтові лінії.

Циліндричною гвинтовою лінією називається лінія, яка розташована на поверхні циліндра та утворена рівномірним рухом точки по твірній, що рівномірно обертається навколо осі циліндра.

Висота циліндра h, на поверхні якого точка здійснює один поворот навколо осі, називається кроком гвинтової лінії.

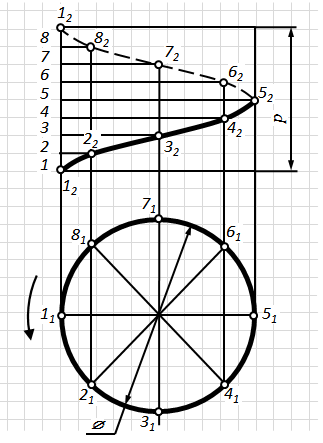Рис.6.11. Побудова циліндричної гвинтової лінії

Гвинтові лінії можуть бути правими і лівими. Правою називається та гвинтова лінія, яка на циліндрі піднімається зліва вгору направо.

Побудову циліндричної гвинтової лінії показано на рис. 6.11.

Задані діаметр гвинтової лінії Ø і крок p.

1. Ділимо коло основи циліндра і крок на однакову кількість рівних частин.

2. Проводимо через перший поділ кроку гвинтової лінії 1 горизонтальну пряму, а через перший поділ 1₁кола – вертикальну пряму.

3. Перетин проведених прямих визначить положення фронтальної проекції 1₂точки, яка перемістилася з початкового положення 0 в положення 1, тобто на одну восьму кроку h.

4. Інші точки 2₂, 3₂– 8₂, які належать фронтальній проекції гвинтової лінії, будуємо аналогічно.

5. Побудовані на П₂точки з'єднуємо плавною кривою.

Рис.6.12. Побудова конічної гвинтової лінії

Побудову конічної гвинтової лінії виконано на рис. 6.12.

Розділимо крок і горизонтальну проекцію конуса на 8 рівних частин.

1. Побудуємо проекції восьми твірних конуса.

2. З першого ділення на П₂проведемо горизонтальну лінію до перетину з першою твірною і позначимо 1₂.

3. Аналогічно будуємо фронтальні проекції всіх восьми положень точки і обводимо їх плавною кривою лінією.

4.Проводячи лінії зв'язку від кожної побудованої на П₂точки до горизонтальної проекції відповідної твірної, визначимо положення горизонтальних проекцій точок і обводимо їх плавною кривою лінією.

6.За різноманітністю форм і властивостей, за своїм значенням при формуванні різних геометричних фігур, за роллю, яку вони відіграють в науці, техніці, архітектурі, поверхні не мають собі рівних серед інших геометричних форм. Світ поверхонь безмежний – від елементарної площини до найскладніших форм криволінійних поверхонь, які не піддаються математичному опису. І якою б складною не була поверхня, її необхідно уміти зображати на кресленні, де повинні бути відображені всі її геометричні властивості.

Розрізняють наступні способи утворення поверхонь:

Рис.6.13. Гіперболічний параболоїд

При цьому поверхня розглядається як геомет-ричне місце точок, координати яких задо-вольняють заданому рівнянню.

Наприклад = 2Z (гіперболічний параболоїд) (рис. 6.13).