А) прямая рекомбинация; б), в) рекомбинация с участием рекомбинационных ловушек.

Рис. 4.10.Расположение уровней ловушек захвата и схематическое изображение процессов захвата электронов и дырок

Прямая рекомбинация происходит при “лобовом” столкновении электрона и дырки. Однако такой процесс прямой рекомбинации мало вероятен, т.к. в одном и том же месте в одно и то же вpемя должны встретиться электpон и дырка, движущиеся с одинаковыми по модулю импульсами в противоположных напpавлениях. Вероятность такой встречи примерно 1/10000.

Чаще всего происходит рекомбинация с участием ловушек. Рекомбинационными ловушками являются глубокие уровни, т.е. уровни достаточно удаленные от краев запрещенной зоны. Такие уровни создают некоторые примеси и дефекты. В этом случае рекомбинация происходит в две стадии, такой процесс более вероятен, так как он не требует одновременного присутствия в данном месте электрона и дырки. Ловушка также воспринимает импульс (количество движения), необходимый для соблюдения закона сохранения импульса, и часть энергии, освобождаемой в процессе рекомбинации. Заметим кстати, что через ловушки может происходить и процесс генерации носителей. При этом направления процессов (направления стрелок) на рис.4.9 следует поменять на противоположные.

Кроме рекомбинационных ловушек, в запрещенной зоне полупроводника могут присутствовать так называемые ловушки захвата (см. рис 4.10) . Это мелкие уровни, способные захватывать носители какого-либо одного типа, а затем через некоторое время возвращать их в ту же зону (электроны – в свободную, дырки – в валентную). Рекомбинация возможна только после освобождения носителя заряда, поэтому наличие ловушек захвата затягивают процесс. Наличие рекомбинационных ловушек и ловушек захвата изменяет вpемя жизни неравновесных носителей.

Распределение электронов и дырок по энергиям в неравновесном случае можно описывать по-прежнему с помощью функции Ферми, но вместо уровня Ферми использовать квазиуровни Ферми, разные для электронов и дырок.

Рассмотрим, как изменяется с течением времени избыточная концентрация неравновесных носителей. Количество носителей, рекомбинирующих в единицу времени в единице объема (быстрота изменения концентрации) пропорциональна избыточной концентрации, коэффициент пропорциональности имеет размерность, обратную размерности времени:

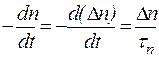, (4.5.1 )

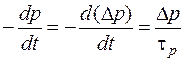, (4.5.2)

где n=n₀+Dn, p=p₀+ Dp – концентрации носителей, Dn, Dp – избыточные концентрации; t_n ,t_p – времена жизни неравновесных носителей.

Из (4.5.1) и (4.5.2) следует, что временем жизни неравновесных носителей заряда называют отношение избыточной концентрации неравновесных носителей к скорости изменения этой концентрации вследствие рекомбинации

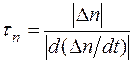, (4.5.3)

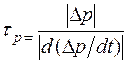. (4.5.4)

В выражения для времен жизни (4.5.3) и (4.5.4) входят концентрации, которые не являются постоянными величинами, следовательно, и времена жизни t_n и t_p тоже непостоянны. Время жизни неравновесных носителей зависит как от факторов, меняющих равновесную концентрацию зарядов в материале, например от температуры, так и от избыточной концентрации.

Рассмотрим наиболее простой случай линейной рекомбинации. В этом частном случае концентрация носителей, с которыми происходит рекомбинация неравновесных носителей, постоянна. Этот случай реализуется, например, в полупроводнике с явно выраженной примесной электропроводностью при введении в него неосновных носителей заряда в небольшом количестве. Тогда появление неравновесных неосновных носителей не вызывает существенного изменения основных, с которыми происходит рекомбинация. Время жизни при этом оказывается постоянным, а количество носителей, рекомбинировавших в единицу времени в единице объема, пропорционально первой степени избыточной концентрации. Уравнения (4.5.1) или (4.5.2) становятся линейными (с этим и связано название данного частного случая рекомбинации):

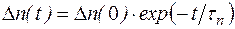; (4.3.13)

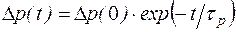, (4.3.14)

то есть в случае линейной рекомбинации время жизни неравновесных носителей – это время, в течение которого их избыточная концентрация уменьшается в e раз.