Коэффициентом диффузии носителей заряда

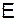Рассмотрим дырочный полупроводник, помещенный в электрическое поле, напряженность которого . Дырки в таком полупроводнике сместятся в направлении поля, возникнет градиент концентрации дырок, и в полупроводнике установится равновесие, при котором ток отсутствует.

Рассмотрим одномерную задачу. Плотность тока можно представить как сумму диффузионной и дрейфовой составляющих, а затем приравнять эту сумму к нулю. Тогда

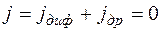; (4.6.1)

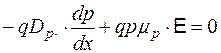. (4.6.2)

Напряженность электрического поля можно представить так:

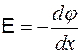, (4.6.3)

где j -потенциал.

Потенциальная энергия дырки равна qj. При отсутствии вырождения распределение дырок в потенциальном поле подчиняется закону Больцмана

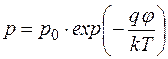, (4.6.4)

откуда

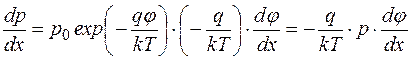. (4.6.5)

Подставляя (4.6.3) и (4.6.5) в (4.6.2), получаем

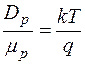. (4.6.6)

Аналогичное выражение можно получить и для электронов:

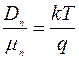. (4.6.7)

Уравнения, связывающие коэффициент диффузии носителей заpяда, подчиняющихся статистике Максвелла-Больцмана, с их дрейфовой подвижностью в условиях термодинамического равновесия носят название соотношений Эйнштейна.

Замечание: Соотношение Эйнштейна применимо и к неравновесным носителям, что подтверждено экспериментально.