А) плотность заряда

Если заряженное тело велико, то нужно знать распределение зарядов внутри тела.

Объемная плотность заряда – измеряется зарядом единицы объема:

Поверхностная плотность заряда – измеряется зарядом единицы поверхности тела (когда заряд распределяется по поверхности):

Линейная плотность заряда (распределение заряда вдоль проводника):

б) вектор электростатической индукции

Вектором электростатической индукции 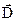(вектором электрического смещения) называется векторная величина, характеризующая электрическое поле.

Вектор 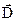равен произведению вектора 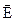на абсолютную диэлектрическую проницаемость среды в данной точке:

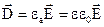
в) поток вектора электростатической индукции

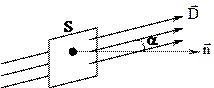N = Sdcosα = SD_n,

где N – поток вектора электростатической индукции, численно равный полному числу линий электрической индукции через эту поверхность

2. Если поле неоднородно, то поверхность разбивают на бесконечно малые элементы dS, которые считают плоскими и поле возле них однородным. Поэтому поток через элемент поверхности равен: dN = D_ndS,

а полный поток через любую поверхность:

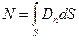
N имеет размерность электрического заряда. Для общего случая, когда поле создается n точечными зарядами:

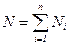
Теорема Остроградского-Гаусса Поток вектора электростатической индукции через любую замкнутую поверхность численно равен алгебраической сумме находящихся внутри этой поверхности зарядов

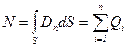
Теорема позволяет найти поток вектора электростатической индукции через замкнутую поверхность, внутри которой находятся электрические заряды, частности Q.

Рассмотрим примеры применения теоремы:

А. Равномерно заряженная плоскость.

Плоскость бесконечная, равномерно заряженная с поверхностной плотностью s. Линии индукции ^ поверхности и по обе стороны.

(9)

Учитывая теорему Остроградского-Гаусса, что поток равен полному заряду, заключенному внутри цилиндра:

N = σS (10)

Решая (9) и (10):

2Ds = σS

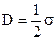
тогда: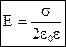

Б. Поле между двумя плоскостями, равномерно с одинаковой плотностью заряженными разноименными зарядами (плоский конденсатор).

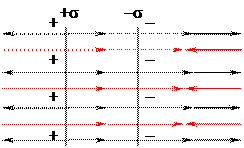
Тогда 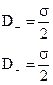Вне пластин Dвн = 0

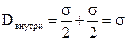
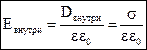
Вывод: Поле сосредоточено внутри конденсатора.

В. Поле, создаваемое заряженной сферической поверхностью.

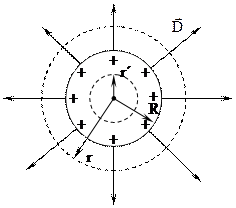
Сферическая поверхность радиуса R с поверхностной плотностью σ+. Выделим мысленно поверхность радиуса r > R, тогда поток вектора электростатической индукции N равен: 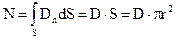(D = Dn, т.к. силовые линии ^ поверхности). Согласно теореме Остроградского-Гаусса:

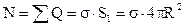
Согласно теореме Остроградского-Гаусса: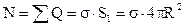

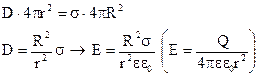если r >> R: 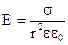r = R :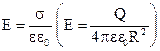

r £ R : E = 0 (т.к. зарядов внутри сферы радиуса r < R нет. Q =0 )

Г. Поле, создаваемое бесконечно длинной равномерно заряженной нитью.

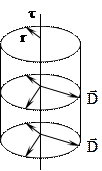
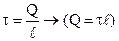Проведем коаксиальную цилиндрическую поверхность радиуса r. Поток через боковую поверхность цилиндра: N = DS = D·2πrℓ Поток по теореме Остроградского-Гаусса: N = Q = τℓ

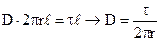
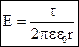
3. Потенциал электростатического поля.

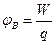
Величина, равная отношению потенциальной энергии заряда к величине заряда, помещенного в данную точку электростатического поля называется потенциалом поля

Если поле образуется несколькими зарядами, то для нахождения потенциала результирующего поля используется принцип суперпозиции: