Законы движения носителей заряда в полупроводниках

В общем случае движение носителей заряда обусловлено двумя процессами: диффузией под действием градиента концентрации и дрейфом под действием градиента электрического потенциала. Поскольку имеются два типа носителей — электроны и дырки, полный ток состоит из четырех составляющих:

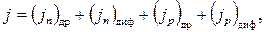(2.29)

где индексы «др» и «диф» относятся соответственно к дрейфовым и диффузионным составляющим тока.

При анализе удобнее пользоваться не токами, а плотностями токов j, что и сделано в формуле (2.29). Там, где это не вызывает недоразумений, будем для краткости называть величину j током.

Составляющие тока. В одномерном случае, когда движение носителей происходит только вдоль оси х, дрейфовые составляющие записываются следующим образом:

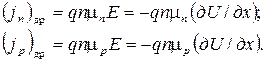(2.30)

где Е – напряженность электрического поля;

U – потенциал.

Тогда диффузионные составляющие токов запишутся следующим образом:

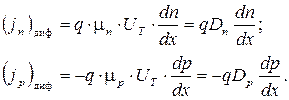(2.31)

где D_n и D_p - коэффициенты диффузии электронов и дырок.

Эти величины играют при диффузии ту же роль, что и подвижности при дрейфовом механизме движения. Связь между коэффициентами диффузии и подвижностями выражается формулой Эйнштейна:

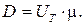(2.32)

Сравнивая выражения (2.30) и (2.31), можно заметить, что дрейфовые составляющие токов пропорциональны концентрациям носителей, тогда как диффузионные не зависят от концентраций, а определяются только градиентами концентрации.

Диффузия носителей. Пусть на поверхность полупроводника падает рассеянный пучок света (рис. 2.9). Тогда в тонком приповерхностном слое, в который проникает свет, будут генерироваться электронно-дырочные пары. Между поверхностью и объемом возникнут градиенты концентрации электронов и дырок и избыточные носители начнут диффундировать вглубь полупроводника. Такое совместное движение обоих типов носителей называют биполярной или амбиполярной диффузией.

Если бы подвижности (а значит, и коэффициенты диффузии) у электронов и дырок были одинаковы, то они двигались бы в виде единого нейтрального потока. На самом же деле подвижности носителей различны, поэтому у электронного потока будет тенденция «обогнать» дырочный поток. В результате небольшого взаимного сдвига потоков образуется небольшой объемный заряд и соответствующее электрическое поле; это поле тормозит поток электронов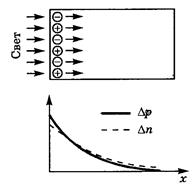

Рис.2.9. Биполярная диффузия, эффект Дембера

и ускоряет поток дырок. В конце концов устанавливается стационарный режим, при котором избыточные электроны и дырки распределены в виде сдвинутых относительно друг друга «облачков». Эти «облачка» двигаются синхронно, так что результирующий ток отсутствует. Концентрация носителей в «облачках» спадает с удалением от поверхности благодаря рекомбинации.

Описанные явления известны под названием эффекта Дембера, а электрическое поле и разность потенциалов, свойственные этому эффекту, называют демберовским полем и демберовским напряжением.

Эффект Дембера существенен только при больших избыточных концентрациях и больших удельных сопротивлениях полупроводников. На практике главную роль играет монополярная диффузия[4], характерная тем, что в приповерхностный слой полупроводника тем или иным способом вводится

только один тип носителей — неосновных, ис.2.10. Процесс введения неосновных носителей называется инжекцией.. Пусть для определенности осуществляется инжекция электронов в дырочный полупроводник. Инжектированные электроны благодаря градиенту концентрации будут диффундировать вглубь кристалла, т.е. появится электронный ток. Заряд избыточных электронов практически мгновенно (со временем диэлектрической релаксации) будет компенсирован таким же зарядом дырок, притягиваемых из глубоких слоев. В результате вблизи инжектирующей поверхности образуется квазинейтральное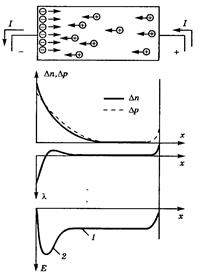

Рис.2.10. Монополярная диффузия; инжекция носителей: 1 – омическое поле; 2- демберовское поле

электронно-дырочное «облачко», почти такое же, как при биполярной диффузии. Несмотря на это внешнее сходство, монополярная диффузия принципиально отличается от биполярной следующими особенностями:

наличие тока предполагает, что полупроводник является элементом замкнутой цели; значит, помимо демберовского поля (сосредоточенного вблизи инжектирующей поверхности) во всей толще полупроводника действует «обычное» —омическое поле, обусловленное приложенным напряжением(рис. 2.10);

потоки электронов и дырок направлены в разные стороны:

электроны двигаются вглубь кристалла, а дырки в сторону инжектирующей поверхности — в район электронно-дырочного «облачка», где происходит интенсивная рекомбинация и необходимо пополнение основных носителей;

в связи с постоянством полного тока его электронная и дырочная составляющие меняются в разные стороны: с удалением от поверхности электронный ток убывает (из-за рекомбинации), а дырочный ток растет; поэтому вдали от поверхности дырочная составляющая — главная и имеет чисто дрейфовый характер (дырки двигаются в поле, созданном внешним напряжением); наоборот, в непосредственной близости от поверхности ток почти чисто электронный и обусловлен диффузией, так как напряженность поля здесь близка к нулю (рис. 2.10).

Величина L, называемая средней диффузионной длиной определяется выражением:

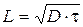(2.33)

L характеризует то среднее расстояние, на которое носители успевают продиффундировать за время жизни.

Поэтому отношение l/τ есть средняя скорость диффузии носителей.

Диффузионная длина — одна из фундаментальных величин в полупроводниковой физике и технике. Для кремния типичные значения L составляют 5-20 мкм в зависимости от времени жизни.

Распределение избыточной концентрации (рис. 2.11,а) примет вид:

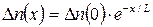(2.34)

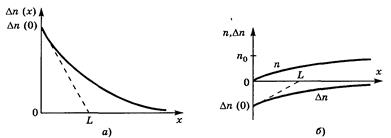
Рис.2.11. Стационарное распределение избыточных носителей

при инжекции (а) и экстракции (б)

Из этого выражения и из рис. 2.11,а следует, что на расстоянии диффузионной длины избыточная концентрация уменьшается в е раз. На участке длиной (3-4)L концентрация уменьшается в 20-50 раз, т.е. становится пренебрежимо малой по сравнению с граничной.

Дифференцируя (2.34), получаем градиент концентрации

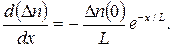(2.35)

Как видим, градиент концентрации, а значит, и диффузионный ток спадают по мере удаления от поверхности вглубь кристалла. Градиент имеет максимальное (по модулю) значение при х = 0, т.е. на инжектирующей поверхности:

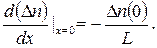(2.36)

Качественные выводы относительно переходного процесса состоят в следующем.

В начальный момент, когда L(0) = 0, градиент концентрации вблизи инжектирующей поверхности согласно (2.36) оказывается бесконечно большим, и, следовательно, избыточные носители будут диффундировать в кристалл с очень большой скоростью.

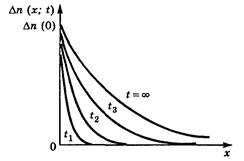
Рис.2.12. Распределение инжектированных

носителей во время переходного процесса

По мере нарастания величины L(t) градиент концентрации на поверхности уменьшается, и скорость диффузии становится все меньше. В конце концов при t ≈ 2τ достигается стационарный режим. Исходя из таких соображений, на рис. 2.12 показаны примерные кривые распределения концентрации для нескольких моментов переходного процесса.

Концентрация неравновесных носителей будет убывать во времени и в пространстве по экспоненциальному закону

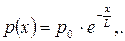
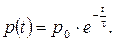(2.37)

Величина 1/τ, обратная времени жизни носителей, будет характеризовать скорость рекомбинации. Скорость рекомбинации будет тем выше, чем выше концентрация основных носителей.