Носители заряда и их распределение в зонах проводимости

Итак, мы подошли к очень важной задаче — определению концентрации носителей заряда в данном полупроводнике при данной температуре.

Так как электроны могут занимать лишь строго определенные энергетические уровни, то ясно, что количество электронов в той или иной зоне не может превосходить числа имеющихся в ней уровней (состояний). Далее, общее число электронов в изолированном объеме полупроводника не может быть ни меньше, ни больше совокупности валентных электронов всех атомов, входящих в данную систему. (Внутренние электронные оболочки мы исключаем из рассмотрения.) Вне зависимости от того, находится ли тот или иной электрон в валентной зоне, в зоне проводимости, на донорном или на акцепторном уровне, общее число электронов будет строго постоянно.

Распределение уровней по энергиям задает один из возможных законов распределения электронов по энергиям, однако распределение электронов по энергиям будет соответствовать распределению уровней по энергиям только в том случае, если все свободные уровни данной зоны будут заняты электронами.

Наиболее простым частным случаем будет идеальный беспримесный кристалл полупроводника, находящийся при температуре абсолютного нуля (0° К). В этом случае всевозможные уровни в валентной зоне будут заполнены и распределение электронов по энергиям будет строго соответствовать закону изменения плотности уровней. Все уровни зоны проводимости будут свободны. В зоне проводимости не будет ни одного электрона. С повышением температуры некоторое количество электронов покидает валентную зону и переходит на уровни зоны проводимости.

Возникает вопрос: какова вероятность того, что тот или иной уровень в зоне проводимости будет занят электроном? Какова вероятность того, что тот или иной уровень валентной зоны лишится своего электрона и превратится в дырку?

Ответ на этот вопрос дает статистика Ферми-Дирака. Согласно статистике Ферми-Дирака вероятность того, что состояние с энергией Е при данной температуре Т занято электроном, выражается функцией Ферми для электронов

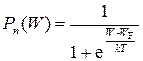, (2.1)

где kT — температурный потенциал;

Т — абсолютная температура;

k — постоянная Больцмана;

W_F — уровень Ферми.

Вероятность выражается в долях единицы. Нетрудно представить, что имеется только две возможности:

1) уровень занят электроном,

2) уровень не занят электроном.

Сумма вероятностей каждого из этих событий должна быть равна единице. Вероятность того, что уровень в валентной зоне не занят электроном, есть вероятность нахождения на этом уровне дырки. Записывая

P_n(W) + P_p(W) = 1,

получаем, что вероятность нахождения дырки на некотором
уровне с энергией W описывается функцией Ферми для
дырок

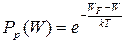
(2.2)

Величина W_F называется энергией или уровнем Ферми.

При любых значениях температуры уровень Ферми совпадает с тем энергетическим уровнем, для которого характерна 50%-ная вероятность занятия (или незанятия) его электроном (при W=W_F, Р_Wn=Р_Wp= 0,5).

Физически уровень Ферми представляет собой химический потенциал электронов данной системы (в расчете на один электрон). Поэтому в дальнейшем мы увидим, что равенство уровней Ферми является обязательным условием равновесия между объемами полупроводника с различным содержанием примесей.

При температуре абсолютного нуля функция Ферми для электронов для всех значений W > W_F (2.1) будет иметь значения, равные нулю. Это значит, что при температуре абсолютного нуля ни один уровень с энергией E > E_F не будет занят электронами. Мы знаем, что при температуре абсолютного нуля все уровни зоны проводимости будут свободны. Отсюда можно сделать вывод, что все уровни зоны проводимости лежат выше уровня Ферми.

Для всех значений W < W_F функция Ферми при Т = 0° К обращается в 1,0. Это, в свою очередь, обозначает, что все уровни с энергиями W < W_F будут заняты. (Вероятность того, что они будут заняты, равна 100%, т. е. превращается в достоверность.) Действительно, в этих условиях полностью заняты все уровни в валентной зоне. Следовательно, все уровни валентной зоны будут лежать ниже уровня Ферми.

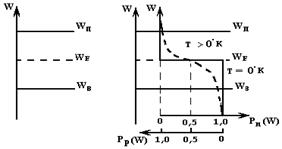
В беспримесном полупроводнике уровень Ферми располагается вблизи середины запрещенной зоны. Положение уровня Ферми и вид функции Ферми при T = 0° К показаны на рис.2.4.

Eсли изменить начало и направление отсчета, то этим же графиком будет изображаться функция Ферми для дырок (P_p(W) = 1 – P_n(W)).

С повышением температуры функция Ферми превращается в плавную кривую. Вероятность нахождений электронов в зоне проводимости становится отличной от нуля. В валентной зоне становится отличной от нуля вероятность появления свободных уровней. Так как кривая симметрична, то эти вероятности оказываются равными.

С повышением температуры вероятность занятия электронами верхних энергетических уровней возрастает. Это объясняется увеличением средней энергии электронов с повышением температуры.

а) б)

Рис. 2.4. Вероятность заполнения P_n(W) или освобождения P_p(W) уровней в чистом полупроводнике:

а) положение уровня Ферми; б) положение функции Ферми для двух значений температуры.

Нас не должно смущать, что значениям энергий, лежащим в запрещенной зоне, соответствуют некоторые значения функции Ферми. Это вовсе не означает, что электроны могут располагаться на уровнях в запрещенной зоне. Мы имеем право пользоваться функцией Ферми только на тех участках, где имеются уровни, разрешенные для электронов. На тех участках, где не имеется разрешенных уровней, функция Ферми не имеет смысла.

Функция Ферми является справедливой не только для «собственных» (т.е. обладающих только собственной электропроводностью, беспримесных) полупроводников. В равной степени этой функцией можно пользоваться и для электронных и для дырочных полупроводников.

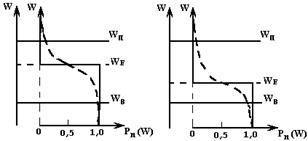
В электронных полупроводниках большое количество электронов переходит в зону проводимости с донорных уровней. Так как появление таких электронов в зоне проводимости не связано с появлением вакантных мест в валентной зоне, то вероятность появления электронов в валентной зоне должна быть выше вероятности появления дырок в зоне проводимости. Очевидно, это будет возможно в том случае, если уровень Ферми W_F сместится в направлении дна зоны проводимости, рис.2.5.а.

а) б)

Рис. 2.5. Вероятность заполнения уровней электронами в примесных полупроводниках:

а) в электронном полупроводнике; б) в дырочном полупроводнике.

Другими словами, средняя энергия электронов в электронном полупроводнике будет несколько выше, чем в собственном полупроводнике, за счет электронов, находящихся на донорных уровнях с повышенным значением энергии. Чем выше концентрация донорных атомов в данном полупроводнике, тем выше будет располагаться уровень Ферми.

Проводя аналогичное рассуждение для дырочного полупроводника, придем к выводу, что в дырочном полупроводнике уровень Ферми должен быть ниже середины запрещенной зоны, причем тем ближе к валентной зоне, чем выше концентрация акцепторов. Положение уровня Ферми относительно середины зоны проводимости ½(W_П + W_В) и смещение функции Ферми для этих двух случаев представлены на рис. 2.5.

В ряде случаев разность (W–W_F) в выражении (1.8) или (W_F –W) в выражении (2.2) более чем в 3 раза превосходит величину kT. Тогда появляется возможность пренебречь единицей по сравнению с экспоненциальным членом в знаменателе, и выражения (2.1) и (2.2) упрощаются:

В этом случае поведение электронов и дырок подчиняется уже не статистике Ферми — Дирака, а классической статистике Максвелла — Больцмана.

Если имеется возможность сделать данное допущение и оценивать процессы в полупроводнике с помощью статистики Максвелла-Больцмана, то полупроводник считается невырожденным. К вырожденным полупроводникам применима только статистика Ферми-Дирака.

В большинстве случаев мы будем иметь дело с невырожденными полупроводниками. Вырождение полупроводника может иметь место в следующих случаях:

1) при достаточно высоких температурах (kT велико);

2) при малой ширине запрещенной зоны (расстояние от уровня Ферми до ближайшего разрешенного уровня составляет 2kT или менее);

3) при сильной степени легирования, когда уровень Ферми приближается к валентной зоне или зоне проводимости на расстояние, меньшее 2kT.

Из этих трех случаев максимальный интерес представляет последний.

Возвращаясь к поставленной задаче о концентрации носителей заряда в данном полупроводнике при данной температуре, определяем, что количество электронов, занимающих разрешенные уровни в некоторой элементарной полосе δW с плотностью уровней N(W), будут определяться числом разрешенных уровней N(W) в данной элементарной полосе δW и вероятностью их заполнения P_n(W)

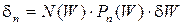
(2.3)

Количество электронов, занимающих уровни в некоторой конечной полосе, ограниченной значениями энергий W₁ и W₂, получим интегрированием

(2.4)

Если определению подлежит количество электронов в зоне проводимости, то пределами интегрирования будут W = W_П — энергия нижнего уровня (дна) зоны проводимости и W = ∞. При определении числа свободных уровней в валентной зоне функцию Ферми для электронов следует заменить функцией Ферми для дырок и интегрировать от W = 0 до W = W_В

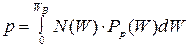
(2.5)

Полагая, что все донорные уровни характеризуются определенным значением энергии W_Д, а акцепторные—W_A и принимая упрощение (2.1а), получаем, что количество электронов, находящихся на донорных уровнях, равно

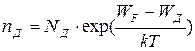
(2.6)

Для расчета количества электронов, занимающих акцепторные уровни, это упрощение не может быть сделано, так как в этом случае экспоненциальная функция в (2.1) мала по сравнению с единицей. В этом случае необходимо пользоваться функцией Ферми.

Для расчета концентрации дырок на акцепторных уровнях может быть принято упрощение (2.2.а).

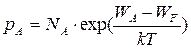
(2.7)

Здесь n_Д и n_a— количество донорных и акцепторных уровней соответственно.

Проводя аналогичные расчеты для электронов в зоне проводимости и для дырок в валентной зоне, получаем

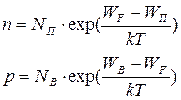
	(2.8)
(2.9)

Здесь N_П — эффективная плотность состояний в зоне проводимости, приведенная к уровню W_П (ко дну зоны проводимости);

N_В — эффективная плотность состояний, приведенная к уровню Е_В (к потолку валентной зоны).

Учитывая, что разность ΔW= W_П – W_В представляет собой ширину запрещенной зоны, а разность ΔW_F = W_F – W_В будет представлять собой расстояние уровня Ферми от потолка валентной зоны, можно преобразовать выражения (2.8) и (2.9) к следующему виду:

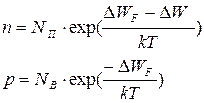
	(2.8.а)
(2.9.а)

В ряде случаев отсчет энергий от потолка валентной зоны оказывается более удобным для практического использования. Отметим, что этими выражениями задается лишь количество электронов и дырок, но не закон их распределения по энергиям в пределах зоны. Напомним, что на основании (2.1.а) и (2.2.а) соотношения (2.8) и (2.9) будут справедливы только для невырожденных полупроводников. Величины N_П и N_В определяются соотношениями

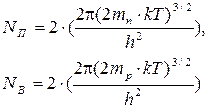
	(2.10)
(2.11)

В эти выражения входят эффективные массы: электронов в зоне проводимости — m_n и дырок в валентной зоне — m_р.

Исходя из условия электрической нейтральности полупроводника, сумма всех зарядов в нем должна быть равна нулю. В собственном, беспримесном полупроводнике количество электронов должно быть равно количеству дырок:

(-q)n+(+q)p=0

n = p

Приравнивая (2.8) и (2.9) и проводя необходимые преобразования, получаем

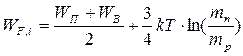
(2.12)

Индекс i обозначает, что данное значение уровня Ферми получено для собственного (intrinsic) полупроводника.

Так как обычно m_п ≠ m_p, то уровень Ферми в собственном полупроводнике будет несколько (весьма незначительно) смещен относительно середины запрещенной зоны. Проводя аналогичные рассуждения для примесных полупроводников, получаем следующие выражения:

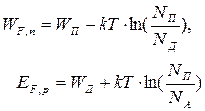
	(2.13)
(2.14)

Концентрацию электронов и дырок в примесном полупроводнике (вне зависимости от типа примеси) можно выразить через уровень Ферми данного полупроводника, уровень Ферми собственного полупроводника и концентрацию носителей в собственном полупроводнике при данной температуре следующим образом:

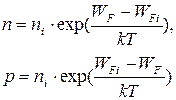
	(2.15)
(2.16)

Перемножая эти выражения, получаем, что

(2.17)

т.е. произведение концентрации дырок на концентрацию электронов в данном полупроводнике при данной температуре есть величина постоянная и не зависит от характера и количества содержащихся в нем примесей. Эта величина всегда равна квадрату концентрации электронов (или дырок, что одно и то же) в беспримесном полупроводнике при той же температуре.