Рекомбинация носителей заряда

Механизмы рекомбинации. Различают непосредственную рекомбинацию и рекомбинацию на примесных центрах.

Непосредственной рекомбинацией называют переход электрона из зоны проводимости непосредственно в валентную зону, где он занимает один из вакантных уровней, т.е. «уничтожает» дырку, рис.2.6.

Рис.2.6. Прямые переходы из зоны в зону.

I-генерация носителей заряда; II-рекомбинация носителей заряда

(а-начальное состояние, б-переход, в –конечное состояние).

Разумеется, при таком переходе должна выделяться энергия qφ_З — такая же, какая была ранее затрачена на перевод электрона из валентной зоны в зону проводимости. Энергия может выделяться либо в виде фотона (излучателъная рекомбинация), либо в виде фонона (безызлучательная рекомбинация). В большинстве полупроводников, в том числе и в кремнии, вероятность излучательной рекомбинации на несколько порядков меньше, чем безызлучательной[2].

Однако вероятность безызлучательной непосредственной рекомбинации сама по себе тоже очень мала, поскольку сравнительно большая энергия qφ_З (порядка 1 эВ) редко может воплотиться в одном фононе, а ее одновременное распределение между двумя фононами маловероятно. Таким образом, непосредственная рекомбинация в целом не является главным механизмом рекомбинации в полупроводниках.

Главную роль играет рекомбинация на примесных центрах. Речь идет о глубоких уровнях, расположенных вблизи середины запрещенной зоны, которые называют ловушками, рис.2.7.

Данный вид рекомбинации — двухэтапный: сначала электрон переходит из зоны проводимости на уровень ловушки, а затем с уровня ловушки в валентную зону. На каждом этапе выделяется энергия, близкая к ½qφ_З Вдвое меньше, чем при непосредственной рекомбинации. Это обстоятельство резко повышает вероятность передачи энергии фонону, что и объясняет преимущественное значение данного механизма рекомбинации.

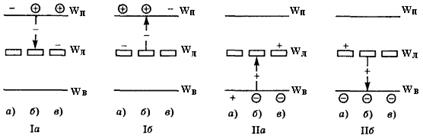
Рис.2.7.

Iа - захват электрона; Iб – отдача электрона;

IIа – захват дырки ( а – начальное состояние; б – переход; в – конечное состояние;

Е_Л – энергетический уровень ловушки)

Роль ловушек могут играть не только примесные атомы, но и различные дефекты решетки. Поэтому повышенная скорость рекомбинации свойственна, в частности, поликристаллам (у которых дефектами являются все грани между отдельными зернами) и приповерхностным слоям любого монокристаллического полупроводника (где неизбежны нарушения периодичности решетки и разрывы ковалентных связей).

Рекомбинация равновесных носителей. Вероятность непосредственной рекомбинации электрона с одной из дырок в единицу времени можно записать следующим образом:

(2.18)

где σ_эфф — эффективное сечение захвата;

V_Т — средняя тепловая скорость электронов[3].

Величину r называют коэффициентом рекомбинации. Умножив коэффициент r на концентрацию дырок, получим полную вероятность рекомбинации электрона в единицу времени (с любой из имеющихся дырок).

Обратная величина будет средним интервалом между актами рекомбинации, т.е. средним временем жизни электронов (дырок) при непосредственной рекомбинации:

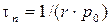(2.19)

.

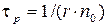В формулах (2.19) индекс «0» присвоен равновесным концентрациям.

Если умножить вероятность рекомбинации одного электрона r^.p₀ на концентрацию электронов n₀, получится общее количество актов рекомбинации в единицу времени, т.е. скорость непосредственной рекомбинации:

R₀=r^.n₀^.p₀ (2.20)

Из формул (2.19) ясно, что равновесные времена жизни электронов и дырок в общем случае резко различны из-за различия концентраций n₀ и p₀, причем время жизни неосновных носителей всегда меньше, чем основных.

Заменяя в правой части (2.19) произведение r^.n₀ на 1/τ_p или r^.p₀ на 1/τ_n , запишем скорость рекомбинации еще в одной распространенной форме:

R₀=p₀/τ_p=n₀/τ_n (2.21)

Непосредственная рекомбинация. В неравновесном состоянии полупроводника концентрации свободных носителей отличаются от равновесных значений:

n = n₀ + ∆n; (2.22)

р= р₀ + ∆р;

Неравновесные концентрации n и р могут быть больше и меньше равновесных, т.е. знаки приращений Δn и Δр в формулах (2.22) могут быть как положительными, так и отрицательными. Приращения Δn и Δр называют избыточными концентрациями. Для сохранения нейтральности полупроводника избыточные концентрации электронов и дырок должны быть одинаковыми:

∆n = ∆p (2.23)

С учетом эквивалентного времени жизни τ представленного в форме соотношения

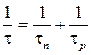(2.24)

от условия равенства скоростей изменения концентраций (2.25)

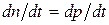(2.25)

перейдем к уравнению рассасывания:

dn/dt= -∆n/ 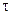(2.26)

Решением уравнения рассасывания является экспоненциальная функция

∆n(t)=∆n(0)^.e^-t/τ , (2.27)

где Δn(0) — начальное значение избыточной концентрации. Зависимость (2.27) позволяет определить время жизни как интервал, в течение которого избыточная концентрация уменьшается в е раз.

Из структуры выражения (2.24) следует, что величина τ близка к минимальной из двух ее составляющих τ_n и τ_p. Следовательно, эквивалентное время жизни избыточных носителей определяется временем жизни неосновных носителей. У электронных полупроводников τ ≈ τ_p, у дырочных τ ≈ τ_n.

Рекомбинация на ловушках. При ловушечном механизме рекомбинации время жизни τ определяется соотношением:

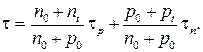(2.28)

Для электронного полупроводника при выполнении свойственных ему неравенств n₀ >> p₀ и n₀ >>n_t, p_t из (2.28) следует:

τ ≈ τ_p. Для дырочного полупроводника при выполнении аналогичных неравенств следует: τ = τ_n. Значит, при ловушечной рекомбинации, как и при непосредственной, время жизни избыточных носителей определяется временем жизни неосновных носителей.

Чем больше концентрация ловушек, тем меньше время жизни.

Зависимость времени жизни от температуры обусловлена резким возрастанием концентрации n_t. Когда величина n_t делается сравнимой с n₀, время жизни начинает увеличиваться, а при условии n_t > n₀ зависимость τ(T) практически совпадает с экспоненциальной функцией n_t(Т). Быстрый рост времени жизни замедляется вблизи критической температуры, когда полупроводник превращается в собственный. Для собственного полупроводника функция τ(T) не нарастающая, а спадающая, так как концентрация n_t, увеличивается медленнее, чем n_i. На рис. 2.8,б показаны примеры функции τ(T) для разных концентраций примеси.

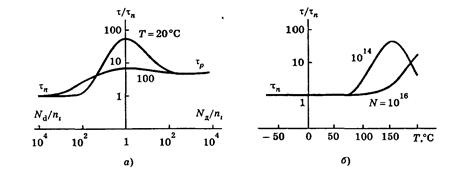
Рис. 2.8. Зависимость времени жизни носителей

от концентрации примеси (а) и от температуры (б)

Как видим, температурная зависимость времени жизни наиболее существенна в слабо легированных полупроводниках (для кремния при N < 10¹⁴–10¹⁵ см^–3). В сильно легированных (низкоомных) полупроводниках эта зависимость второстепенная.

В заключение отметим, что типичные значения времени жизни для кремния составляют 0,1—1 мкс. Если специально легировать кремний «ловушечной» примесью (чаще всего золотом), то время жизни уменьшается до 10 нc и менее.