КОМПЛЕКСНЕ КРЕСЛЕННЯ ПЛОЩИНИ

1. Площиною називається поверхня, що утворена рухом прямої лінії паралельно самій собі по прямолінійній напрямній.

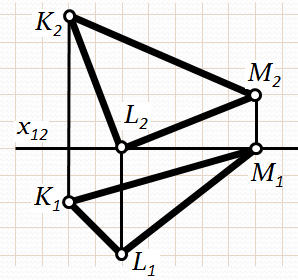Рис.3.1. Відсік площини

1) трьох точок, що не лежать на одній прямій (рис.3.2-а);

2) прямої і точки, розташованої поза нею (рис.3.2-б);

3) двох прямих, що перетинаються (рис.3.2-в);

4) двох паралельних прямих (рис.3.2-г);

5) відсіку площини (трикутника або іншої плоскої фігури) (рис.3.2);

6) слідами площини (рис. 3.4).

а) б) в) г)

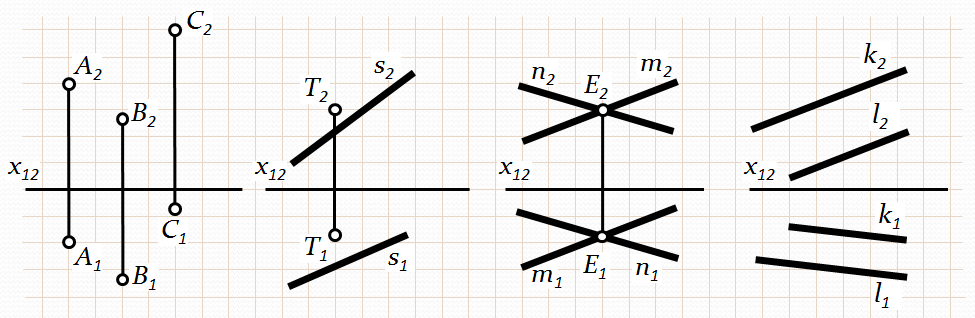
Рис. 3.2. Способи задавання площини

2. У деяких випадках площину доцільно задавати не довільними прямими, що перетинаються, а прямими, по яких ця площина перетинає площини проекцій.

Рис.3.2. До визначення слідів площини

На рисунку 3.3 показано зображення площини на комплексному кресленні за допомогою слідів h⁰(h⁰₁, h⁰₂) і f ⁰(f ⁰₁, f ⁰₂). Проекції слідів f ⁰₁i h⁰₂збігаються з віссю Х₁₂.

Рис.3.3. Комплексне креслення площини заданої слідами

h⁰(h⁰₁, h⁰₂): h⁰ Ì П₁Þ h⁰ º h⁰₁;

h⁰₂завжди належить осі Х₁₂.

Фронтальний слід

f ⁰(f ⁰₁, f⁰₂): f ⁰ Ì П₂Þ f ⁰ º f⁰₂;

f ⁰₁завжди належить осі Х₁₂.

Точка збігу слідів площини Х^S (Х^S=S Ç Х₁₂) належить осі проекцій (Х^SÎХ₁₂), тобто Х^S º Х^S₁º Х^S₂, а тому позначаємо її як точку, а не як проекцію.

Для того, щоб побудувати слід площини на епбрі необхідно і достатньо побудувати сліди двох прямих, які лежать в цій площині (рис. 3.3).

Рис. 3.4. Побудова слідів площини

3. За розташуванням у просторі розрізняють площини окремого і загального положення. Площини окремого положення поділяють на площини рівня і проецюючі.

Площиною рівня називається площина, яка паралельна одній і перпендикулярна до двох інших площин проекцій. Розрізняють три види площин рівня:

горизонтальну (рис.3.5-а) – паралельну площині проекцій П₁і перпендикулярну до П₂та П₃;

фронтальну (рис.3.5-б) – паралельну площині проекцій П₂і перпен-дикулярну до П₁та П₃;

профільну (рис.3.5-в) – паралельну площині проекцій П₃і перпен-дикулярну до П₁та П₂.

Проецюючою площиною називається площина, яка перпендикулярна до однієї з площин проекцій. Розрізняють три види проецюючих площин:

горизонтально-проецюючу (рис.3.6-а) – перпендикулярну площині проекцій П₁;

фронтально-проецюючу(рис.3.6-б) – перпендикулярну площині проекцій П₂;

профільно-проецюючу (рис.3.6-в) – перпендикулярну площині проекцій П₂.

а)

б)

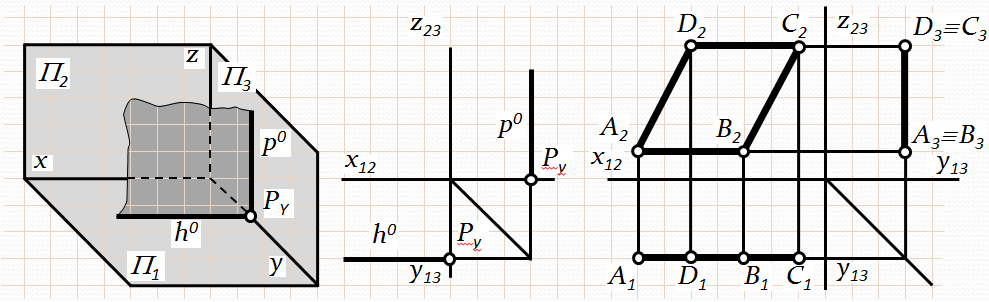
в)

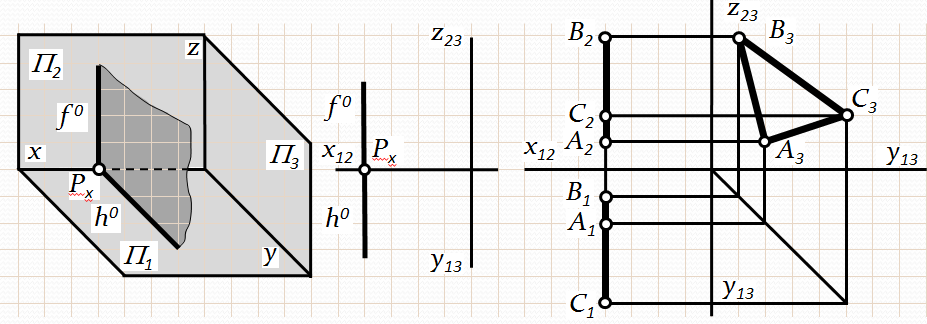
Рис. 3.5. Площини рівня

Проекційні ознаки площин рівня:

1) Довільна фігура, що лежить у площині рівня, проецюється в натуральну величину на ту площину, якій ця площина рівня паралельна. На дві інші площини проекцій вона проецюється відрізками прямих (слідами-проекціями площин рівня), які займають вертикальне або горизонтальне положення.

2) Сліди-проекції площин рівня мають збиральну властивість, яка полягає в тому, що проекції точок, ліній, фігур, що лежать у цих площинах, розташовуються на слідах-проекціях.

а)

б)

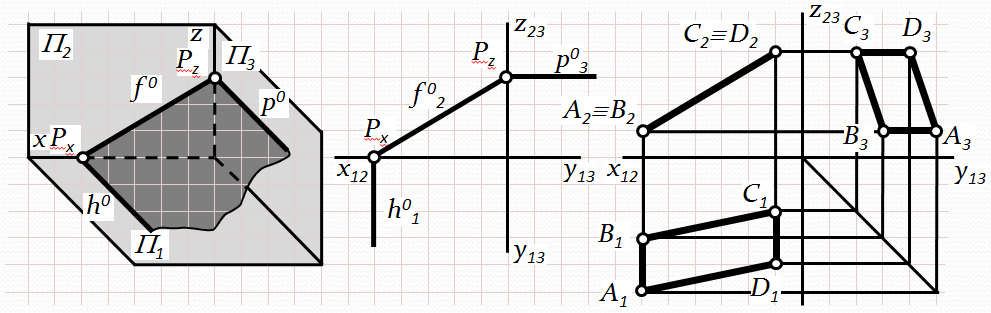
в)

Рис. 3.6. Проецюючі площини

Основні проекційні ознаки проецюючих площин:

1) Проецююча площина зображується слідом-проекцією на перпендикулярній до неї площині проекцій. На двох інших площинах проекцій фігура, що лежить у проецюючій площині, зображається спотворено.

2) Проецюючу площину можна задати лише одним слідом-проекцією, який має збиральну властивість (точки, лінії, фігури, що належать проецюючій площині, проецюються на слід-проекію цієї площини).

Площина, яка не перпендикулярна ні одній із площин проекцій (рис. 3.7, 3.8) називається площиною загального положення.

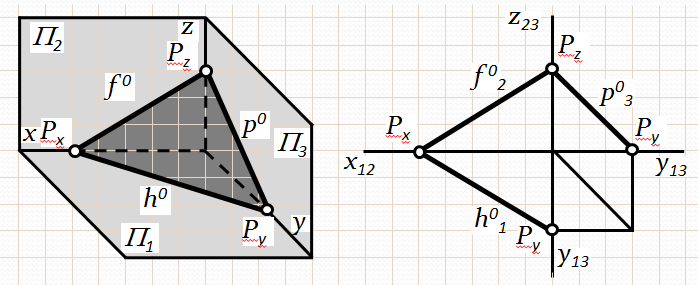
Рис. 3.7. Комплексне креслення площини загального положення

Рис.3.8. Епюр площини загального положення

Всі три проекції площини загального положення являють собою трикутники. Така площина має три сліди на площинах проекцій, які не являються перпендикулярними жодній осі проекцій.

4. Пряма належить площині, якщо вона проходить через дві точки, що належать цій площині, або через одну її точку паралельно іншій прямій, проведеній на площині.

Рис. 3.19. Приналежність прямої площині

Для того, щоб на комплексному кресленні площини, заданої слідами провести будь-яку пряму загального положення (рис.3.10), необхідно намітити на слідах площини дві точки (1 і 2), та вважати їх слідами шуканої прямої. Опустивши перпендикуляри з цих точок на вісь проекцій Ох, знаходимо на ній другі проекції слідів прямої. З'єднавши однойменні проекції отримаємо дві проекції прямої лінії розташованої в площині загального положення.

Рис. 3.10. Побудова прямої на комплексному кресленні площини

Точка належить площині, якщо вона лежить на прямій, що належить цій площині. Для визначення відсутньої проекції точки, яка лежить у площині необхідно спочатку побудувати проекції прямої, яка проходить через цю точку і лежить у площині і на цих проекціях прямої позначити проекції точки (рис. 3.11).

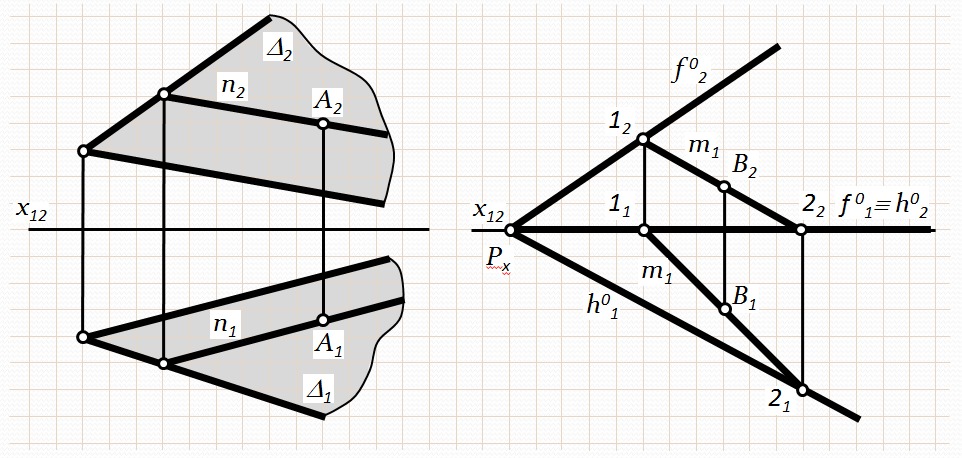
Рис. 3.11. Приналежність точки площині

5. В площині загального положення можна провести безліч прямих, які по відношенню до площин проекцій можуть займати окреме і загальне положення.

Горизонталлю площини (h) називається горизонталь, яка належить цій площині.

Рис.3.12. Головні лінії площини

Фронталлю площини(f) називається фронталь, що належить цій площині. Побудову фронталі площини (рис. 3.12) починаємо з проведення її горизонтальної проекції f₁(А₁2₁) яка паралельна осі Х₁₂. Всі фронтальні прямі проведені в площині паралельні між собою та нульовій фронталі (фронтальному сліду площини f ⁰).

Для того щоб на комплексному кресленні площини, яка задана слідами, провести в цій площині горизонталь (рис.3.13-а), необхідно намітити на фронтальному сліді площини f ⁰₂точку (1 º 1₂), та вважати її фронтальною проекцією фронтального сліду горизонталі. Потім через точку паралельно осі х₁₂проводимо пряму, що буде фронтальною проекцією горизонталі (h₂). Горизонтальну проекція горизонталі проводиться паралельно h⁰₁через горизонтальну проекцію точки 1 (1₁).

Аналогічно виконуються побудови для знаходження фронталі (рис.3.13-б).

а)

б)

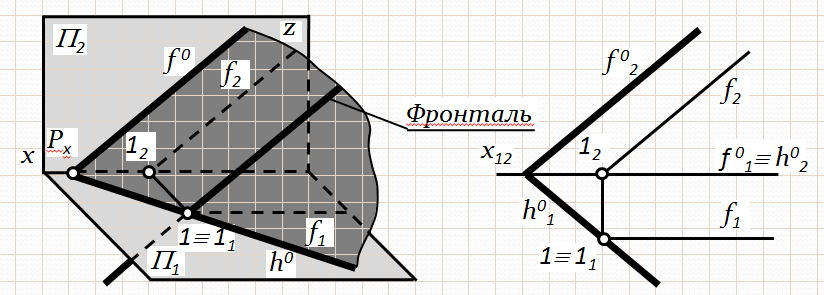
Рис. 3.13. Побудова горизонталі і фронталі на комплексному кресленні площини

Профільною прямою площини (р) називається пряма, що належить цій площині і паралельна профільній площині проекцій. Її проекції на П₁і П₂завжди перпендикулярні осі Х₁₂(рис. 3.12).

Лініями найбільшого нахилу площини до площин проекцій називаються прямі, що лежать у площині і перпендикулярні до ліній рівня площини (слідів площини). Для побудови ліній найбільшого нахилу площини (ЛНН) необхідно побудувати лінії рівня площини, а потім – лінії найбільшого нахилу.

У площині розрізняють лінії найбільшого нахилу:

1) ЛНН відносно П₁визначає нахил площини до П₁і має ще одну назву: лінія скату; відмітною особливістю лінії найбільшого нахилу до П₁є перпендикулярність її горизонтальної проекції до горизонтальної проекції горизонталі площини чи до її горизонтального сліду (ЛНН)₁ ^ h₁;

2) ЛНН відносно П₂(рис.3.17) визначає нахил площини до П₂; відмітною особливістю ЛНН до П₂є перпендикулярність її фронтальної проекції до фронтальної проекції фронталі площини чи до її фронтального сліду (ЛНН)₂ ^ f₂;

3) ЛНН відносно П₃визначає нахил площини до П₃; відмітною особливістю ЛНН до П₃є перпендикулярність її профільної проекції до профільної проекції профільної прямої площини чи до її профільного сліду (ЛНН)₃^ р₃.

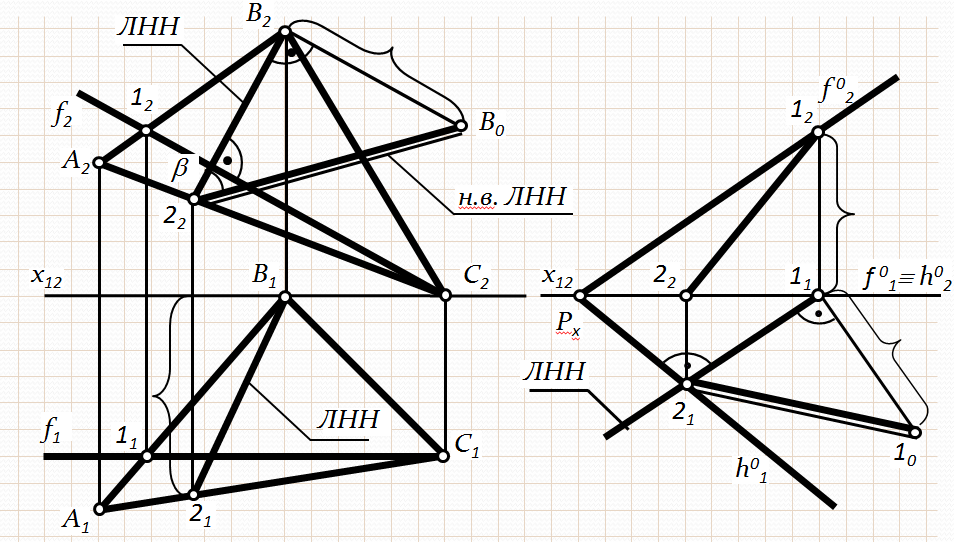
Рис. 3.17. Побудова ЛНН на комплексному кресленні площини