Взаємне положення прямої і площини

Пряма може належатиплощині або перетинати її. Якщо пряма перетинає площину в нескінченно вилученій точці, вважається, що пряма буде паралельна площини.

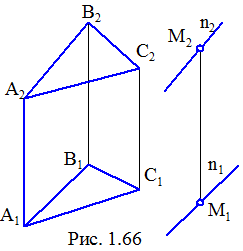
Пряма паралельна площині, якщо вона паралельна деякій прямій цієї площини. Тому, для того, щоб через задану точку простору М провести пряму, паралельну площині Σ (АВС) (рис. 1. 66), необхідно провести її паралельно деякій прямій у площині, наприклад, АВ (n₂ ‖A₂B₂; n₁‖A₁B₁).

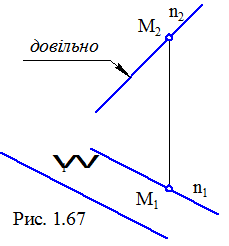Для того щоб провести пряму паралельно площині особливого положення, необхідно її проекцію провести паралельно до відповідного сліда-проекції площини(рис. 1. 67). Положення другої проекції може бути задане довільно, але не вертикально, якщо пряма на наявній проекції не проекціюється в точку.

Пряма перетинає площину в точці. Ця точка належить одночасно цим двом геометричним образам. Побудова точки перетину залежить від положення, що займають ці образи щодо площин проекцій. Виділимо кілька типових випадків.

1. Пряма й площина є проекціюючі (рис. 1.68, а). Проекції точки перетину перебувають на слідах-проекціях прямої й площині.

2. Один геометричний образ займає проекціююче положення, а другий – загальне. У цьому випадку, одна проекція точки перетину лежить на сліді-проекції того образа, що займає проекціююче положення, а друга визначається приналежністю образу, що займає загальне положення.

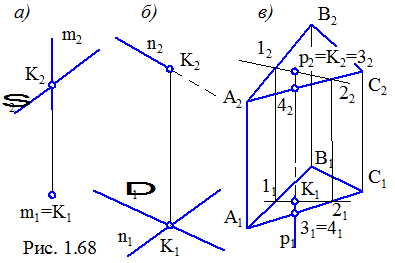На рис. 1.68, б пряма n займає загальне положення, а площина Δ – горизонтально-проекціююче. Горизонтальна проекція К₁ точки перетину К лежить на сліді-проекції Δ₁ площини Δ. Фронтальна проекція – К₂ визначається перетином вертикальної лінії зв'язку із фронтальною проекцією n₂ прямої.

На рис. 1.68, в пряма p займає фронтально-проекціююче положення, а площина, що задана трикутником АВС, – загальне. Фронтальна проекція точки перетину К₂ збігається зі слідом-проекцією прямої, а горизонтальна проекція К₁ визначається за правилом приналежності точки площині, тобто вона повинна розміщатись на довільній прямій цієї площини, наприклад, на лінії 12.

Для визначення видимості прямої p відносно площини, вибирають дві конкуруючі точки, наприклад, 3 і 4 на мимобіжних прямих АС і p. Нехай точка 3 належить прямій р, а точка 4 – АС. Горизонтальні проекції цих прямих збігаються, а фронтальна проекція точки 4 розташована нижче фронтальної проекції точки 3. Отже, пряма p у цьому місці на горизонтальній площині проекцій не буде закрита площиною трикутника. Зміна видимості прямої на зворотне відбувається у точці перетину К.

3. Розглянемо спосіб рішення завдань на визначення точки перетину геометричних образів, що одночасно займають загальне положення.

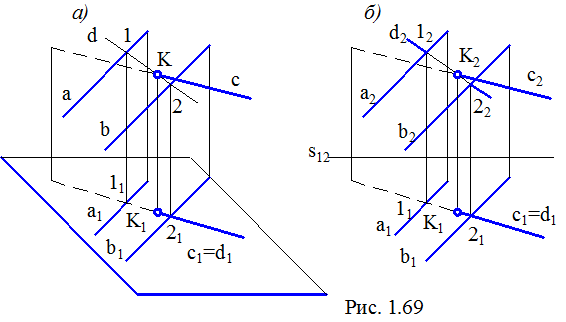
На рис. 1.69, а представлені довільно розташовані в просторі площина Г (a, b), що задана двома паралельними прямими, і пряма с. У площині Г (a, b) виберемо деяку пряму d, що конкурує з прямою с стосовно горизонтальної площини проекцій. У таких прямих горизонтальні проекції збігаються (с₁=d₁), а в просторі ці прямі будуть перетинатися. Точка їхнього перетину К буде одночасно належати і прямій с і площині Г (a, b), тобто вона й буде точкою перетину прямої з площиною.

На кресленні (рис. 1.69, б) побудови варто починати з того, що на однієї з проекцій (у нашому прикладі – на горизонтальній) укажемо пряму d, горизонтальна проекція якої збігається з горизонтальною проекцією прямої с, тобто (с₁=d₁). По двом точкам побудуємо фронтальну проекцію прямої d і у місці перетину їхніх фронтальних проекцій відзначимо шукану точку К.

В окремих випадках пряма може виявитися перпендикулярною до площини. Відомо, що пряма перпендикулярна до площини, якщо вона перпендикулярна двом не паралельним між собою прямим цієї площини. Розглянемо три характерних випадки розташування площини й перпендикуляра до неї.

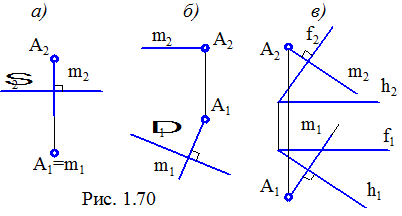Пряма, що перпендикулярна до площини рівня, займає проекціююче положення (рис. 1.70, а).

Пряма, що перпендикулярна до проекціюючої площини, є лінією рівня (рис. 1.70, б).

Ці випадки легко собі представити, промоделювавши їх за допомогою олівця й картону.