Точка і пряма в площині

При рішенні різних завдань, пов'язаних із зображеннями, виникає необхідність у побудові на кресленнях точок, ліній і плоских фігур, що належать будь-якої площини. Для побудови проекцій цих об'єктів використають відомі з геометріі визначення з деякими змінами, що враховують особливості проекційних креслень.

Так, точка належить площині, якщо вона належить до прямої, яка розташована в цій площині. Якщо пряма є визначником площини і вона вже є на кресленні, то на її проекціях з заданих умов будують відповідні проекції точки, використовуючи відоме правило (точка належить до прямої, якщо її проекції лежать на відповідних проекціях прямої). Частіше такої прямої на кресленні ще немає і її необхідно побудувати. Для цієї мети використовують наступне правило: пряма належить площині, якщо вона проходить через дві точки, що лежать у площині. Найчастіше ці точки беруть на визначниках площини.

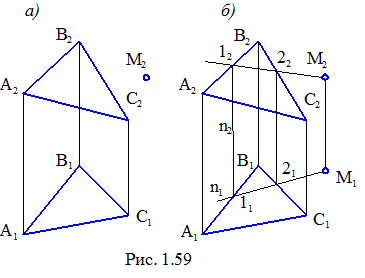
Приклад. Нехай площина Σ задана на кресленні проекціями трикутника АВС і також є фронтальна проекція точки М (рис. 1.59, а). Необхідно побудувати її горизонтальну проекцію, якщо відомо, що вона належить площині Σ (АВС).

Рішення (рис. 1.59, б). Через М₂ проводять фронтальну проекцію довільно розташованої прямої n. На цій прямій виділяють дві точки 1 і 2, що лежать на визначнику площини. Точка 1 належить відрізку АС, точка 2 – відрізку ВС. По лініям зв'язку будують їхні горизонтальні проекції, а потім горизонтальну проекцію лінії n – n₁. На її перетині з лінією зв'язку, проведеної з точки М₂, визначають горизонтальну проекцію шуканої точки.

Крім цього, пряма належить площині, якщо вона проходить через одну точку площини і паралельна прямої, яка розташована в цій площині.

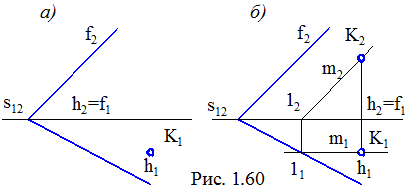Приклад. Побудувати точку К, що належить площині Г (h, f), якщо задана її горизонтальна проекція (рис. 1.60, а).

Рішення (рис. 1.60, б). Через точку К проводять лінію m, яка паралельна f, тому її горизонтальна проекція m₁ буде розташована паралельно f₁, тобто горизонтально. На цій лінії виділяють точку 1, що належить до площини Г (лежить на визначнику площини – лінії h). Фронтальна проекція лінії m буде розташовуватися паралельно фронтальній проекції лінії f. За допомогою лінії зв'язку визначають фронтальну проекцію точки К.

Відзначимо, що лінія m належить площині Г і паралельна фронтальній площині проекцій. Така лінія зветься фронталлю площини. Це одна з головних ліній площини. До таких, крім названої, відносять горизонталь, профільну пряму й лінії найбільшого нахилу. Називані лініями рівня горизонталь, фронталь і профільна пряма належать площині і одночасно паралельні відповідним основним площинам проекцій, а лінії найбільшого нахилу розташовані в площині і перпендикулярні цим лініям.

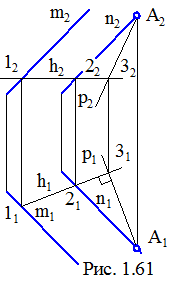
На рис. 1.61, як приклад, у площині загального положення, заданої довільними паралельними прямими m і n, побудована горизонталь h, а, потім, з точки А, що лежить у площині, перпендикулярно горизонталі проведена лінія найбільшого нахилу р.

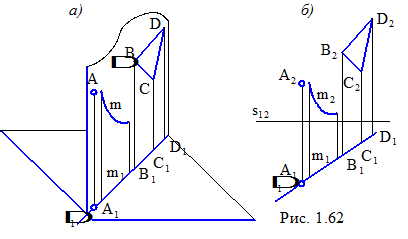
Розглянемо особливості розташування точок, ліній і плоских фігур у площинах особливого положення. Раніше відзначалося, що ці площини мають збірну властивість. Проілюструємо цю важливу властивість на прикладі горизонтально-проекціюючої площини Δ (рис. 1.62, а, б). У цій площині розташовані точка А, плоска крива m і плоска фігура – трикутник ВСD. Положення площини Δ збігається з напрямком проектування на горизонтальну площину проекцій, тому, як відомо, вона зобразиться на площину П₁ у вигляді прямої лінії. На цій лінії і будуть розташовуватися горизонтальні проекції перерахованих вище елементів.

Не менш важливим представляється й зворотне положення: якщо проекція якого-небудь елемента (точки, лінії або плоского багатокутника) лежить на відповідному сліді-проекції площини, то він належить цій площині.

Підкреслюємо, правило обмовляє тільки приналежність до площини особливого положення, ні форму цього елемента, ні його конкретне положення в просторі по одній проекції визначити не можливо. Правило є основним при рішенні багатьох завдань, наприклад, для знаходження загальних елементів двох пересічних геометричних образів.

◊ Побудувати пряму m по одній її проекції (див. рис), якщо відомо, що вона належить площині Σ.

◊ Задайте проекціями довільну площину загального положення й побудуйте в цій площині точку на висоті 30 мм і на глибині 10 мм.