Нанесення розмірів на кресленнях плоских фігур

Для будь-якого предмета розміри на його кресленні можна розділити на дві групи. До першої віднесемо ті з них, які визначають положення предмета в просторі, до другої – розміри, що фіксують положення одних частин предмета відносно інших.

Перша група розмірів закріплює положення предмета відносно деякої початкової системи відліку. В інженерній графіці це, як відомо, площини проекцій, які крім своєї основної ролі, грають ще й роль такої системи.

Таким чином, для вказівки положення точки в просторі достатньо вказати її відстань до трьох взаємно перпендикулярних площин. На практиці цю систему розмірів у повному обсязі використовують рідко, а обмежуються лише частиною, наприклад, визначають відстань або кут нахилу тільки до однієї з площин проекцій. Ще частіше предмет лише орієнтують що до площин проекцій, створюючи у такий спосіб умови зручного нанесення розмірів, що координують зв'язок одних елементів відносно інших у самому предметі.

Нанесення розмірів на плоскій фігурі, що визначають її форму й положення щодо площин проекцій, залежить у першу чергу, від розташування площини, у якій ця фігура перебуває. Тому, до часу вивчення цього матеріалу, дуже важливо вміти орієнтуватися в розташуванні формотворних елементів у просторі.

Нагадаємо, що розміри можуть бути поставлені на ті елементи плоского відсіку, які не піддалися спотворенню при проекціюванні його на площину проекцій. Як правило, це будуть відрізки ліній і плоскі фігури, що займають особливе положення.

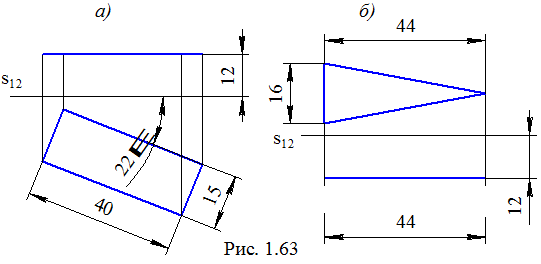Для приклада розглянемо нанесення розмірів, що визначають форму й розташування двох багатокутників: рівнобедреного трикутника і прямокутнка, що займають різне положення, що до основних площин проекцій.

Якщо плоска фігура займає положення площини рівня, це дозволяє на її зображенні, розташованому на площині проекцій, їй паралельній, поставити будь-який лінійний і кутовий розмір, тому що будь-яка лінія, що обмежує фігуру, займає особливе положення (рис. 1.63, а). Для нанесення лінійних розмірів може бути використаний і слід-проекція фігури, якщо в цьому є необхідність (розмір 44 на рис. 1.63, б дублює аналогічний на виді спереду; на кресленні, природно, виставляється тільки один з них). При такому розташуванні плоских фігур не важко вказати й розміри, що фіксують їх відносно площин проекцій. Виходячи з того, що паралельність і перпендикулярність на кресленнях не обговорюють розмірами, а визначають візуально, то достатньо вказати лінійний розмір відстані до площини проекцій – 12 мм, що розташовується паралельно площини багатогранника. Для орієнтації прямокутника (рис. 1.63, а) показано кут нахилу однієї його сторони до площини проекцій П₂.

На фігурі, що лежить у проекціюючій площині, можна вказати лінійні розміри тільки на лініях, розташованих паралельно і перпендикулярно сліду-проекції. Зважаючи на це, фігури у таких площинах прагнуть розмістити так, щоб прямі, які є їхніми складовими, розташовувалися особливим образом щодо площин проекцій (рис. 1.64). Усі кутові розміри в проекціюючих площинах, спотворюються. Виключення становлять прямі кути, але за умови, що одна їхня сторона паралельна площини проекцій. Для проекціюючих площин, можна вказати кут нахилу їх до площини проекцій.

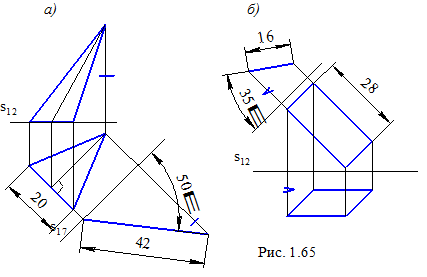Якщо фігура лежить у площині загального положення, то можуть бути зазначені лише лінійні розміри, що є відрізками ліній рівня. На рис. 1. 65, а показано рівнобедрений трикутник, підстава якого займає горизонтальне положення. Висота трикутника, що перпендикулярна підставі, є лінією загального положення, її істинна величина може бути знайдена на допоміжній площині проекцій. Будучи лінією найбільшого нахилу, вона характеризує кут нахилу площини до горизонтальної площини проекцій.

На рис. 1.65, б у площині загального положення взято прямокутник, дві сторони якого є фронталями, а дві інші – загального положення. Величина останніх сторін може бути знайдена тільки на додатковій площині проекцій, таким само чином і кут нахилу площини до П₂.

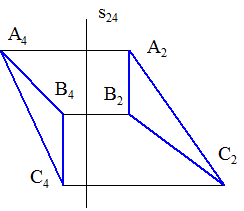
◊ Розміри яких сторін трикутника АВС і на яких зображеннях можна поставити на запропонованому кресленні?

◊ Визначіть кутовий розмір нахилу площини трикутника АВС до фронтальної площини проекцій.