ВЗАЄМНЕ ПОЛОЖЕННЯ ГЕОМЕТРИЧНИХ ФІГУР

1.Точка належить прямій, коли її однойменні проекції лежать на однойменних проекціях прямої і знаходяться у проекційному зв’язку. Тому належність точки прямій загального положення достатньо перевірити на двох її проекціях В лекції №2, п. 2.2 було розглянуто можливі варіанти взаємного положення точки і прямої (рис. 2.9).

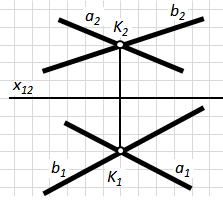Рис.4.1. Взаємний перетин двох прямих

Якщо прямі перетинаються в просторі, то на епюрі (рис. 3.1) перетинаються їх однойменні проекції. Проекції точок перетину прямих знаходяться у проекційному зв’язку.

Якщо одна з прямих, що перетинаються являється лінією рівня, то перевірка перетину прямих проводиться у цій площині проекцій, до якої лінія рівня паралельна.

Якщо прямі в просторі паралельні, то їх однойменні проекції на будь-яку площину також взаємно паралельні а₁ІІ b₁, a₂II b₂(рис.4.2-а).

Перевірку прямих загального положення на паралельність достатньо провести на двох проекціях. Паралельність прямих рівня, перевіряють на тій площині проекцій, до якої ці прямі паралельні.

а) б)

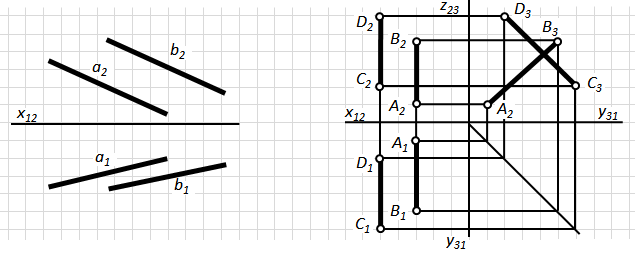
Рис. 4.2. Взаємне положення прямих в просторі

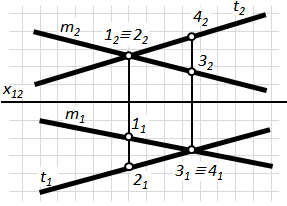Рис.4.3. Мимобіжні прямі

Прямі, які в просторі не паралельні між собою і не перетинаються називаються мимобіжними. Точки перетину однойменних проекцій цих прямих не лежать на одній лінії проекційного зв’язку (рис.4.2-б, 4.3) та називаються конкуруючими точками (детальніше ознайомлення див. лекція №1 п. 1.6).

Загальним випадком взаєм-ного положення прямої і площини є їх перетин. Якщо точка перетину знаходиться у нескінченності, то пряма і площина паралельні між собою (рис.4.4).

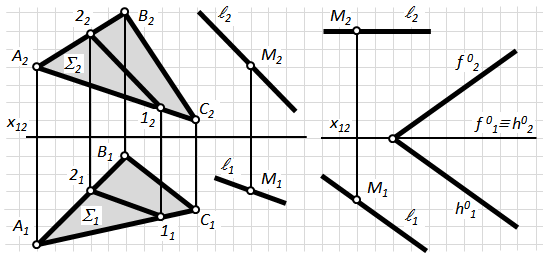
Рис.4.4. Паралельність прямої та площини

Пряма паралельна площині, якщо вона паралельна якій-небудь прямій, розміщеній на цій площині.

Якщо через точку в просторі треба провести пряму, паралельну площині, то спочатку в цій площині проводимо яку-небудь пряму, а потім через задану точку проводимо другу пряму, паралельну першій (рис.4.4).

Побудова точки зустрічі прямої загального положення з площиною загального положення складається з трьох операцій (рис.4.5):

1. Проведення через задану пряму c допоміжної площини-посередника Q (зазвичай проецююча площина).

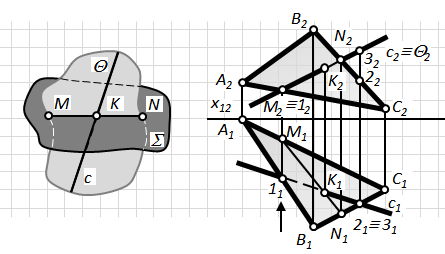
Рис.4.5. Перетин прямої та площини

2. Знаходження лінії MN перерізу заданої площини S з допоміжною площиною Q.

3. Визначення точки K перетину заданої прямої c зі знайденою лінією перерізу двох площин. Точка K є шуканою точкою перетину прямої c з площиною S.

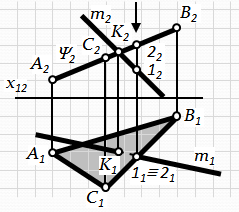Рис.4.6. Перетин прямої з проецюючою площиною

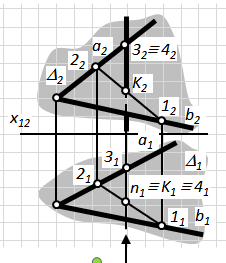Рис.4.7. Перетин проецюючої прямої з площиною загального положення

Загальним випадком взаємного положення двох площин є їх переріз. Якщо лінія перерізу знаходиться в нескінченності, то площини будуть паралельні між собою.

Площини паралельні(рис.4.8), якщо дві прямі, що перетинаються, однієї з них відповідно паралельні двом прямим, що перетинаються, другої.

Площини окремого положення паралельні тоді, коли паралельні їх однойменні сліди-проекції (рис.4.8-б).

Щоб побудувати через задану точку K площину, паралельну площині S (а Ç b), досить через точку K провести дві прямі, відповідно паралельні двом прямим, що перетинаються і належать площині S (рис.4.8).

а) б)

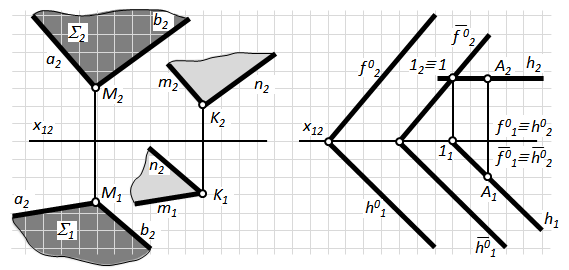
Рис.4.8. Паралельність площин в просторі

Дві площини, перпендикулярні до якої-небудь площини проекцій, перетинаються по прямій, яка перпендикулярна до тієї самої площини проекцій (рис.4.9-а).

Дві площини, які перпендикулярні до різних площин проекцій, перерізаються по прямій, проекції якої збігаються зі слідами-проекціями площин (рис.4.9-б).

а) б)

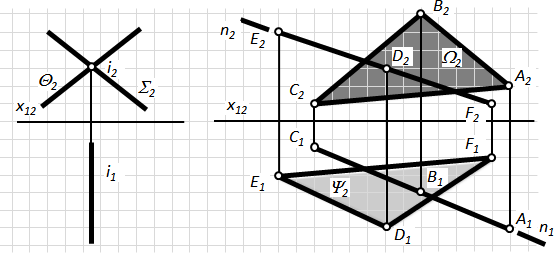
Рис.4.9. Перетин площин окремого положення

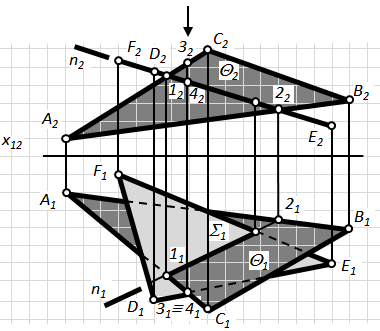Рис.4.10. Взаємне положення площин в просторі

Розглянемо випадок перетину двох площин загального положення (рис. 4.11). Дві площини перетинаються по прямій лінії, а положення прямої цілком визначається двома точками. Тому розв'язання задачі на побудову проекцій прямої перетину двох площин у загальному випадку зводиться до визначення проекцій двох точок, які одночасно належать кожній з площин, що перетинаються. Лінія перетину площин пройде через ці дві точки.

Задачу можна розв'язати двома способами:

- способом знаходження точки зустрічі прямої з площиною;

- способом допоміжних січних площин (метод посередника).

Суть метода посередника:

а) дві задані площини перетинаються третьою допоміжною площиною-посередником;

б) будується лінія перетину кожної з заданих площин з посередником;

в) знаходиться точка, в якій перетинаються ці лінії перетину і яка є однією з точок шуканої лінії перетину заданих площин.

Нехай задано дві площини загального положення S (DАВС) та Q (a ІІ b). Необхідно знайти лінію перетину площин S Ç Q = n( MN).

1) Вводимо допоміжну фронтально-проецюючу площину L – L ^ П₂;

L Î a; a Ç S = M; L Ç S = l ; l₂ º a₂º L₂; l₁Ç a₁= M₁Þ M₂.

2) Вводимо допоміжну фронтально-проецюючу площину Ф – Ф ^ П2; Ф Ç S = t ( т. 3,4); Ф Ç Q =c (т. 5, 6);

d Ç t = N ; Ф₂º c₂º t₂º N₂; d₁Ç t₁= N₁.

3) Видимість площин на П₁і П₂визначаємо за допомогою т. 7, 8 і 9, 10

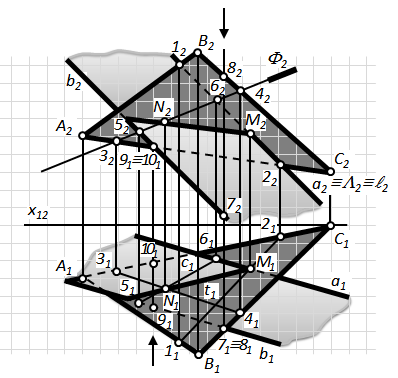
Рис.4.11. Перетин площин загального положення

2.Для того, щоб ортогональна проекція прямого кута на яку-небудь площину проекцій була прямим кутом (проеціювалася в натуральну величину), необхідно і досить, щоб хоча б одна зі сторін цього кута була паралельною площині проекцій, в той час, як інша сторона не повинна бути перпендикулярною до цієї площини проекцій.

Ð ABC = 90°: BC ІІ П₀Þ Ð A₀B₀C₀=90°.

Доведемо це. Продовжимо АВ до перетину з площиною П₀в точці K º K₀. Через точку K₀в площині П₀проведемо пряму q₀ІІ B₀C₀. Оскільки q₀ ІІ B₀C₀, а B₀C₀ІІ BC, то q₀ІІ BC. Звідси кут BK₀L₀= 90°. Згідно з теоремою про три перпендикуляри (пряма, яка належить площині, тоді і тільки тоді перпендикулярна похилій до цієї площини, коли вона перпендикулярна до її проекції на розглядувану площину) кут B₀K₀L₀теж прямий. Через те, що K₀L₀ ІІ B₀C₀, а кут B₀K₀L₀= 90° і кут K₀B₀C₀= 90°.

а) б)

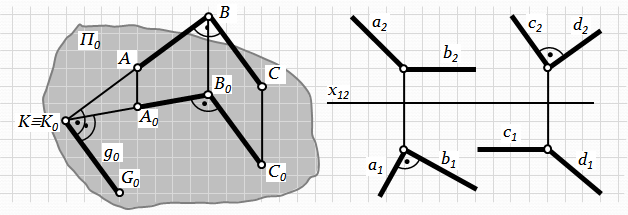
Рис.4.12.

Висновок:

1) якщо проекція плоского кута являє собою прямий кут, то проецюючий кут буде прямим лише за умови, що хоча б одна зі сторін цього кута паралельна площині проекцій (рис. 4.12-б).

2) якщо проекція будь-якого кута, у якого одна із сторін паралельна площині проекцій, являє собою прямий кут, то кут, що проецюється, теж буде прямим (рис. 4.12-б).

Теорема про проеціювання прямого кута є теоретичною передумовою для побудови на комплексному кресленні проекцій прямих і площин, взаємно перпендикулярних у просторі.

3. Знаходження відстані між двома прямими зводиться до розв'язання задачі на визначення відстані від точки до прямої, оскільки саме відстань від точки до прямої визначається довжиною відрізка перпендикуляра, проведеного з точки на пряму.

Розглянемо три випадки.

Випадок 1. Пряма ί^ П₂(П₁); точка А.

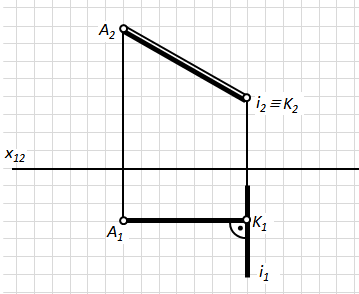Рис.4.13.

Являючись фронталь-но-проецюючою, (рис. 4.13) пряма ί водночас є горизонталлю, а тому на П₁вона зберігає свою перпендикулярність з перпендикуляром, опущеним з точки А на неї. Таким чином, на комплексному кресленні А₁K₁^ ί₁. Очевидно, що АK – фронталь, а тому А₂K₂– натуральна величина відрізка перпендикуляра АK.

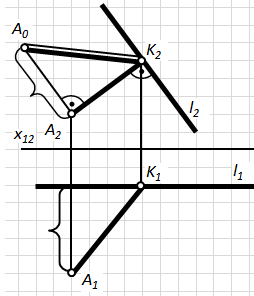Рис.4.14.

Оскільки пряма l – фронтальна (рис. 4.14), то на площині проекцій П₂вона збереже перпендикулярність з перпендикуляром, проведеним до неї з точки А: А₂К₂ ^ l₂.

З комплексного креслення очевидно, що відрізок АK – загального положення, а тому його натуральну величину визначаємо способом прямокутного трикутника.

Випадок 3.Пряма l загального положення; точка А (рис. 5.13).

Якщо пряма займає загальне положення то для визначення відстані від точки до прямої використовуємо відому з геометрії теорему: дві прямі взаємно перпендикулярні тільки в тому випадку, якщо через кожну з них можна провести площину, перпендикулярну до другої прямої.

1) Через точку А проводимо площину S, яка буде перпендикулярною до прямої l. А Î S; S ^ l. S(h Ç f); h₁^ l₁, f₂^ l₂.

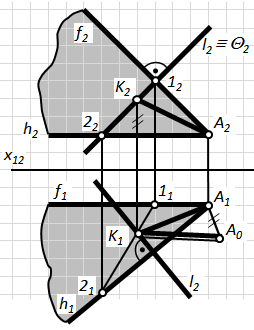Рис.4.15.

3) Способом прямокутного трикутника визначаємо натуральну величину відрізка АК.