КОМПЛЕКСНЕ КРЕСЛЕННЯ ПРЯМОЇ.

1. Пряма в інженерній графіці розглядається як множина точок.

Пряма в просторі безмежна. Обмежена частина прямої називається відрізком.

При ортогональному проеціюванні на площину пряма, не перпендикулярна до площини проекцій, проецюється в пряму.

Оскільки положення прямої у просторі повністю визначається двома точками, то для визначення проекцій прямої досить визначити проекції будь-яких двох точок, які належать цій прямій.

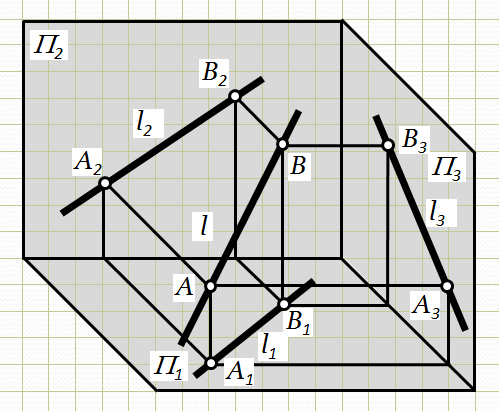Рис.2.1. Пряма в системі трьох площин проекцій

Відрізок А₁В₁– гори-зонтальна проекція відрізка АВ, А₂В₂– його фронтальна проекція; А₃В₃– його профільна проекція.

Пряму на комплексному кресленні можна задати не тільки проекціями її відрізка (АВ), але і проекціями деякої довільної частини прямої (l), не позначаючи кінцевих точок цієї частини.

Зазвичай третю площину проекцій П₃розглядають тільки як додаткову площину, тому що положення точки у просторі однозначно визначається двома її проекціями. Таким чином, дві проекції прямої повністю визначають її положення у просторі.

Для перетворення просторового макета у плоске комплексне креслення площину проекцій П₁необхідно повернути навколо осі Х₁₂на кут 90° за годинниковою стрілкою і провести перпендикуляри до осі Х₁₂з проекцій точок А і В – А₁А₂; B₁B₂ (вертикальні лінії зв'язку).

Прямі в просторі можуть займати різні положення. Розрізняють наступні положення прямих: прямі загального положення; прямі рівня; проецюючі прямі

Відрізок АВ займає довільне (загальне) положення по відношенню до площин проекцій П₁, П₂, П₃(тобто кути нахилу відрізка АВ до П₁, П₂, П₃довільні, але відмінні від 0° і 90°) (рис. 2.2). Така пряма називається прямою загального положення. На комплексному кресленні проекції прямої загального положення складають з осями проекцій також довільні кути. Координати будь-якої точки прямої загального положення – мінливі величини: немає таких двох точок, для яких хоча б одна координата була однаковою.

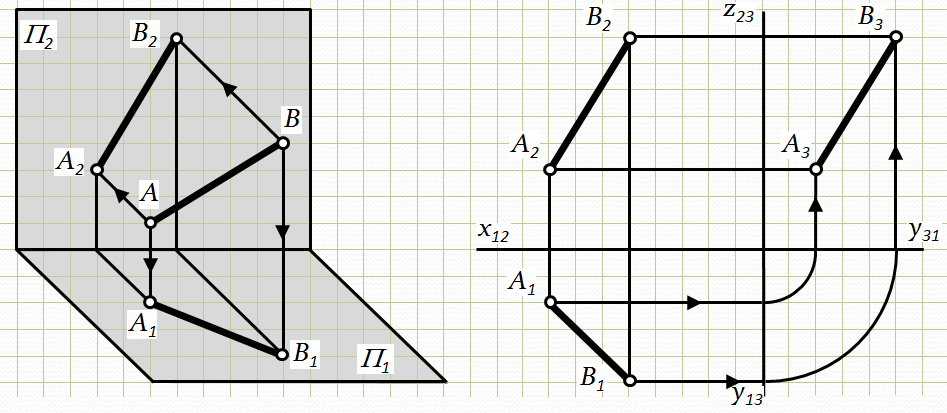
Рис.2.2. Епюр прямої загального положення

Окрім розглянутого загального випадку розміщення прямої по відношенню до заданої системи площин проекцій, існують окремі (часткові) випадки.

Прямі, паралельні до площин проекцій, називаються лініями рівня.

Горизонтальна пряма (горизонталь) – це пряма, паралельна до горизонтальної площини проекцій. Вона позначається літерою h (h₁, h₂, h₃) (на рис. 2.3 відрізок АВ паралельний до П₁). Усі точки горизонталі віддалені на однакові відстані від П₁, тобто для усіх точок горизонталі координата Z – величина постійна (Z = const). А тому h₂II Х₁₂(h₂^ Z₂₃, h₃^ Z₂₃).

Кут нахилу горизонталі до П₁– a = 0°. Кут нахилу горизонталі до П₂– b і кут нахилу до П₃– g визначаються з горизонтальної проекції h – h₁(А₁В₁) (рис. 2.3).

На площину проекцій П₁відрізки прямої h проецюються в натуральну величину, а на дві інші площини – зі спотворенням, у вигляді відрізків меншої величини.

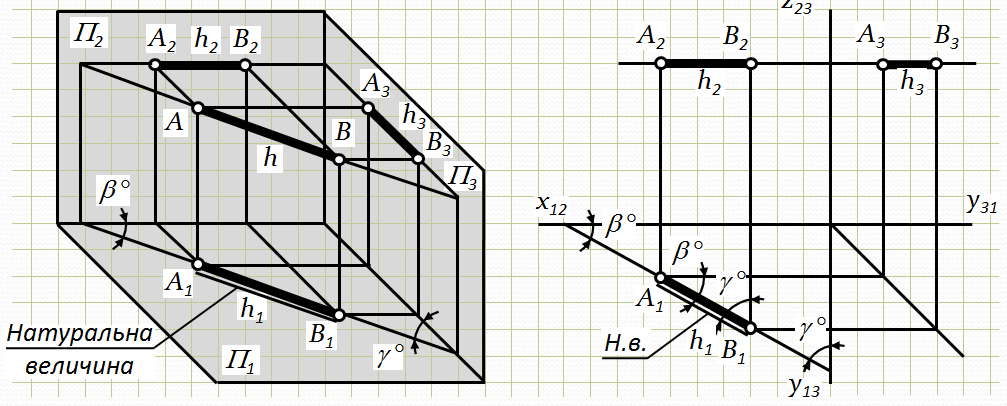
Рис.2.3. Епюр горизонтальної прямої

hII П₁: a = 0Þ П₁; b Þ П₂; g Þ П₃

Фронтальна пряма (фронталь) – це пряма, паралельна до фронтальної площини проекцій. Вона позначається літерою f(f₁, f₂, f₃) (на рис. 2.4 відрізок СD паралельний до П₂). Усі точки фронталі віддалені на однакові відстані від П₂, тобто для усіх точок фронталі координата Y – величина постійна (Y = const). А тому f₁II Х₁₂ (f₁^ Y₁₃, f₃^ Y₃₁).

Кут нахилу фронтальної прямої до П₂– b = 0°. Кут нахилу фронталі до П₁– a і кут нахилу до П₃– g визначаються з фронтальної проекції f – f₂(С₂D₂) (рис. 2.4).

На площину П₂відрізки прямої f проецюються в натуральну величину, а на дві інші площини – зі спотворенням, у вигляді відрізків меншої величини.

fII П₂: a Þ П₁; b = 0 Þ П₂; g Þ П₃

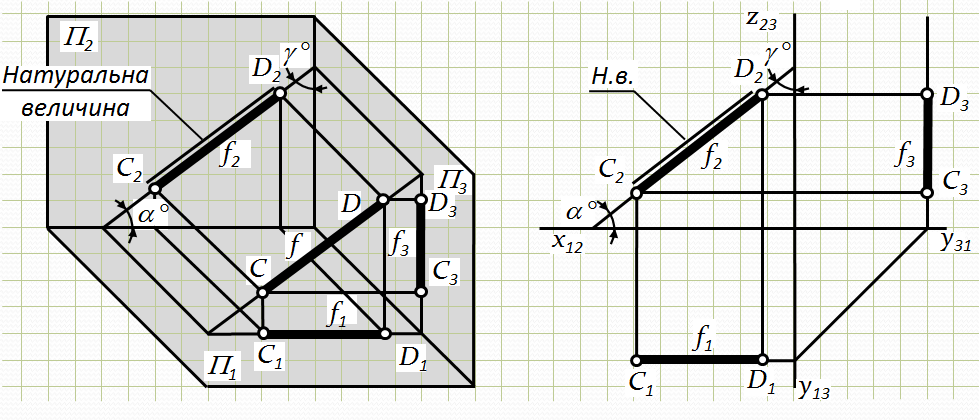
Рис.2.4. Епюр фронтальної прямої

Профільна пряма – це пряма, паралельна до профільної площини проекцій. Вона позначається літерою р (р₁, р₂, р₃) (на рис. 2.5 відрізок EF паралельний до П₃). Усі точки профільної прямої віддалені на однакові відстані від П₃, тобто для усіх точок профільної прямої координата Х – величина постійна (Х = const). А тому р₁^ Х₁₂, р₂^ Х₁₂(р₁II Y₁₃, р₂II Z₂₃).

Кут нахилу профільної прямої до П₃– g = 0°. Кут нахилу профільної прямої до П₁– a і кут нахилу до П₂– b визначаються з профільної проекції р – р₃(Е₃F₃) (рис. 2.5).

На профільну площину проекцій П₃відрізки прямої р проецюються в натуральну величину, а на дві інші площини – зі спотворенням,у вигляді відрізків меншої величини, які перпендикулярні осі Х₁₂.

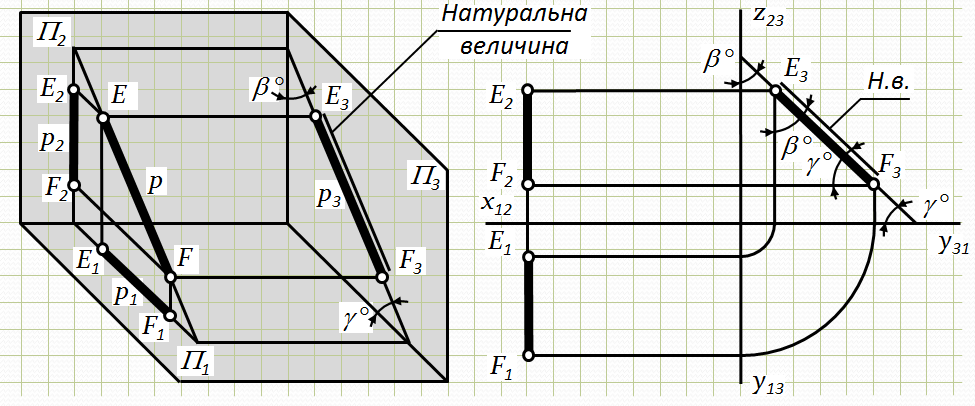
Рис.2.4. Епюр профільної прямої

р II П₃: a Þ П₁; b Þ П₂; g = 0 Þ П₃.

Пряма може бути не тільки паралельною до площини проекцій, але і знаходитись у ній. Характерною ознакою комплексного креслення такої прямої є належність однієї з проекцій такої прямої осі проекцій (рис. 2.5), де h⁰ – нульова горизонталь; f ⁰ – нульова фронталь.

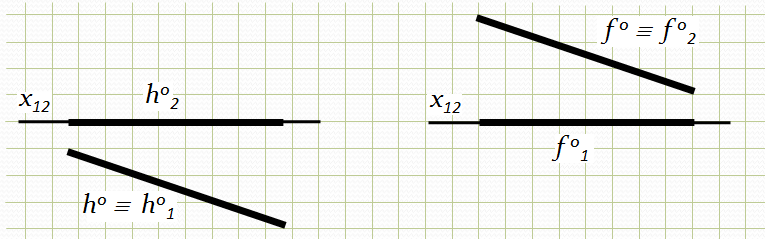
Рис.2.5. Пряма, що належить площині проекцій

Проецюючими називаються прямі які перпендикулярні до однієї з площин проекцій і паралельні двом іншим площинам проекцій (рис. 2.6-2.8). На одній з площин проекцій проецююча пряма зображується у вигляді точки, а на двох інших - у вигляді відрізків, які займають горизонтальне або вертикальне положення і величина яких дорівнює натуральній величині відрізка прямої.

Пряма а ^ П₁– горизонтально проецююча пряма. Вона проецюється на горизонтальну площину в точку, а на фронтальну і профільну площини проекцій – в лінію, паралельну осі Oz.

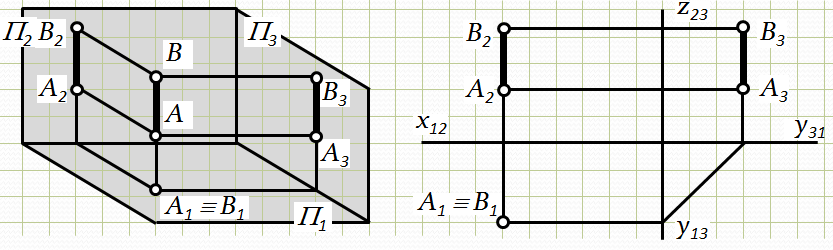
Рис.2.6. Епюр горизонтально-проецюючої прямої

Пряма СD ^ П₂– фронтально проецююча пряма. Ця пряма проецюється в точку на фронтальну площину проекцій, а на горизонтальну і профільну площини проекцій – в лінію, паралельну осі Оу.

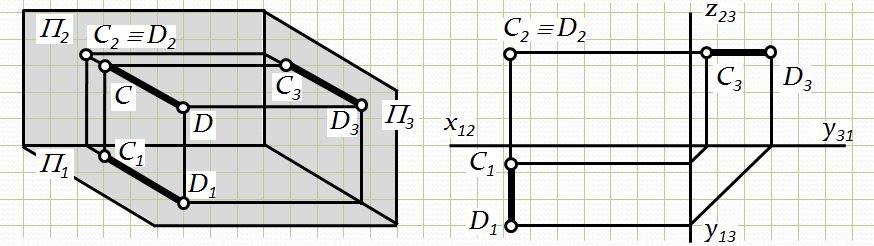
Рис.2.7. Епюр фронтально-проецюючої прямої

Пряма EF ^ П₃– профільно проецююча пряма. Пряма проецюється в точку на профільну площину проекцій, а її горизонтальна і фронтальна проекції паралельні осі Ох.

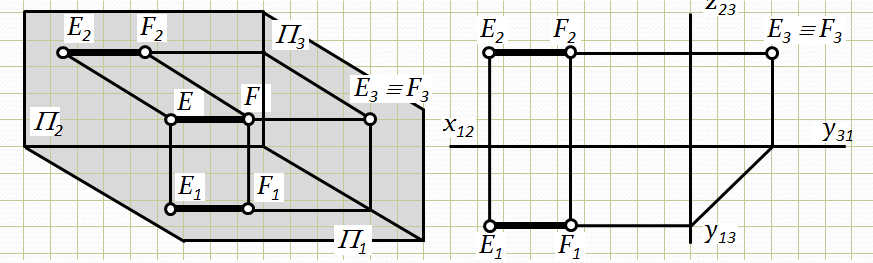
Рис.2.8. Епюр профільно-проецюючої прямої

2. Якщо точка лежить на прямій, то її проекції лежать на однойменних проекціях цієї прямої і на спільній лінії зв’язку.

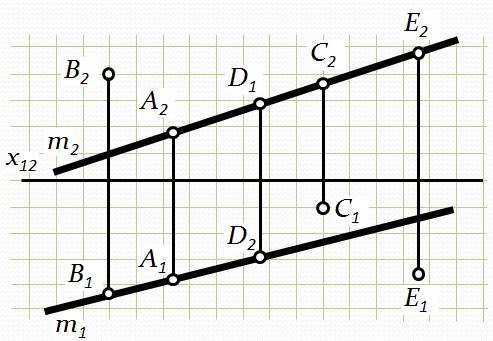Рис.2.9. Положення точки на прямій

Точки В,С, D i E не лежать на прямій m, тому що одна з проекцій кожної точки не належить відповідній проекції цієї прямої.

Точка, яка не лежить на прямій відносно прямої може займати різне положення. Наприклад: точка В знаходиться над прямою m, точка Е – під прямою m, точка С – за прямою m.

3. Пряма загального положення перетинає всі основні площини проекцій. Якщо відрізок АВ загального положення продовжити в обидва боки від точок А і В, то він перетне площини проекцій П₁і П₁в точках М і N (рис. 2.10).

Точки перетину прямої з площинами проекцій називаються слідами прямої. Точка М – горизонтальний слід прямої АВ, а точка N – фронтальний слід прямої АВ.

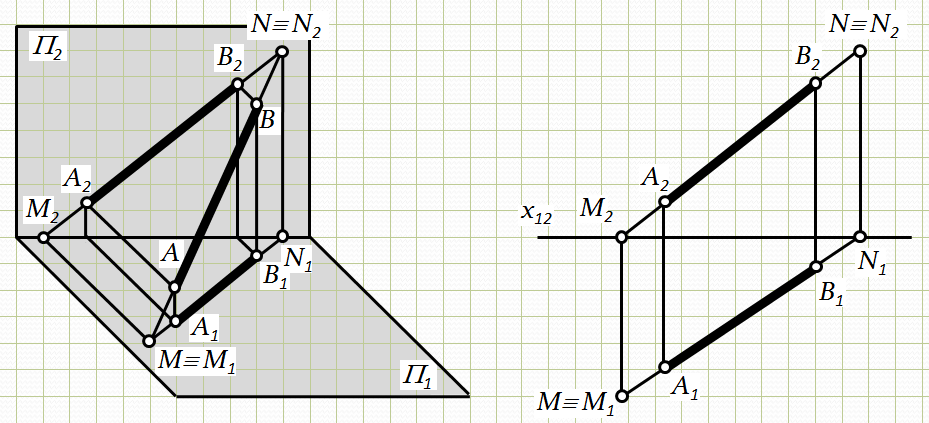
Рис.2.10. Побудова слідів прямої загального положення

Слід– це точка, яка одночасно належить прямій і площині проекцій. З цієї умови витікає правило побудови слідів прямої. Побудувати сліди прямої на комплексному кресленні означає – знайти проекції слідів.

Горизонтальний слід прямої – це точка, яка належить прямій, а тому її проекції належать проекціям прямої. З іншого боку ця точка належить і площині проекцій П₁, тому вона має особливості точок, які належать площинам проекцій: одна координата дорівнює нулю. Для точки, яка лежить на П₁– Z = 0. Точка прямої АВ, для якої Z = 0, на комплексному кресленні (рис. 2.10) знаходиться на перетині фронтальної проекції прямої АВ (А₂В₂) з віссю Х₁₂. Це точка М₂– фронтальна проекція горизонтального сліду прямої. Точка М₁знаходиться на одній вертикальній лінії зв'язку з М₂і належить горизонтальній проекції прямої.

Таким чином, для побудови на комплексному кресленні горизонтального сліду М прямої АВ необхідно:

1). Продовжити фронтальну проекцію А₂В₂до перетину з віссю Х₁₂в точці М₂. Точка М₂– фронтальна проекція сліду М.

2). Провести через точку М₂вертикальну лінію зв’язку до перетину з горизонтальною проекцією А₁В₁прямої (або її продовженням) в точці М₁(горизонтальній проекції сліду), яка збігається з самим слідом М.

Фронтальний слід прямої– це точка, яка належить прямій, а тому її проекції належать проекціям прямої. З іншого боку ця точка належить і площині проекцій П₂, тому вона має особливості точок, які належать площинам проекцій: одна координата дорівнює нулю. Для точки, яка лежить на П₂– Y = 0. Точка прямої АВ, для якої Y = 0, на комплексному кресленні (рис. 2.10) знаходиться на перетині горизонтальної проекції прямої АВ (А₁В₁) з віссю Х₁₂. Це N₁– горизонтальна проекція фронтального сліду прямої. N₂знаходиться на одній вертикальній лінії зв'язку з N₁і належить фронтальній проекції прямої.

Таким чином, для побудови фронтального сліду (точки N) прямої АВ необхідно:

1). Продовжити горизонтальну проекцію А₁В₁до перетину з віссю Х₁₂в точці N₁. Точка N₁– горизонтальна проекція сліду N.

2). Провести через точку N₁ вертикальну лінію зв’язку до перетину з фронтальною проекцією А₂В₂прямої (або її продовженням). Отримаємо точку N₂(фронтальну проекцію сліду) яка збігається з самим слідом N.

Пряма загального положення в системі трьох площин проекцій має три сліди: горизонтальний, фронтальний і профільний; пряма рівня - два сліди; проецююча пряма – один слід. На рисунку 2.11-а показана побудова фронтального сліду N і профільного сліду Р горизонталі h, а також горизонтального сліду М і профільного сліду Р фронталі f (рис. 2.11-б).

а) б)

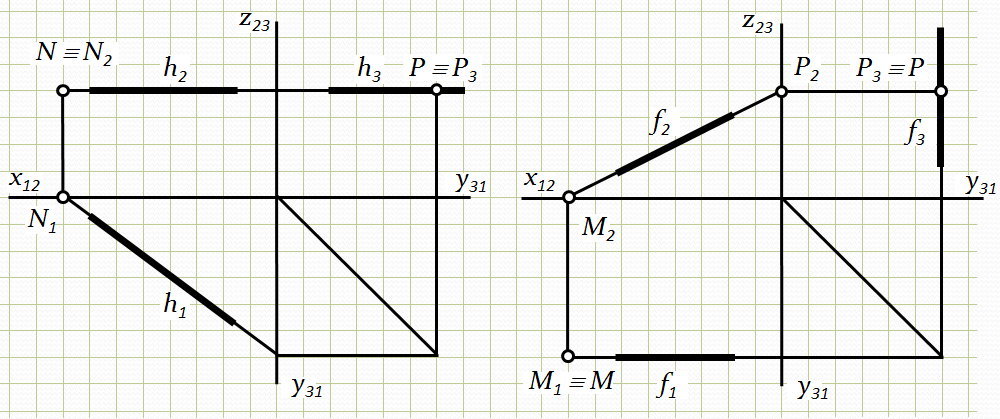
Рис.2.11. Побудова слідів прямих рівня

Горизонтально-проецююча пряма а має один горизонтальний слід М (М₁), який збігається з горизонтальною проекцією прямої а (рис. 2.12-а).

Фронтально-проецююча пряма b має один фронтальний слід N (N₂), який збігається з фронтальною проекцією прямої b (рис. 2.12-б).

а) б)

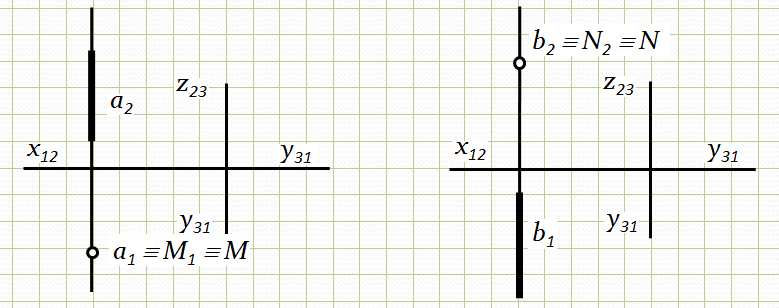
Рис.2.12. Побудова слідів проецюючих прямих

4. Пряма загального положення нахилена під різними кутами до площин проекцій, а тому проекції відрізка прямої різні за величиною і важливо уміти знаходити натуральну величину відрізка прямої за його проекціями.

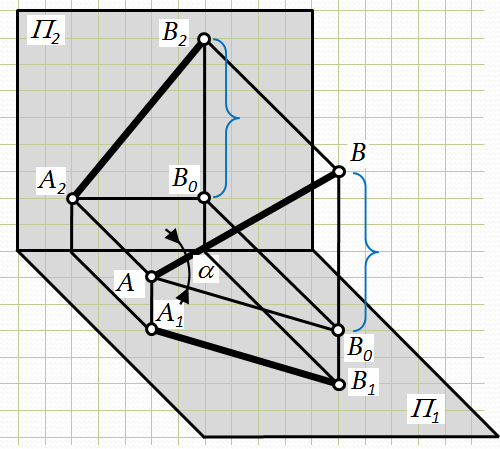Рис.2.13. До визначення натуральної величини відрізка

Оскільки АВ₀IIА₁В₁; АВ₀^ВВ₁, Þ |А₁В₁| = |АВ₀| – катет АВ₀дорівнює горизон-тальній проекції відрізка АВ. Другий катет ВВ₀дорівнює різниці висот між точками В і А: |ВВ₀| = Z_B – Z_A.

α – кут між гіпотенузою і катетом АВ₀, тобто між відрізком АВ і його проекцією на П₁є кутом нахилу відрізка прямої АВ до площини проекцій П₁.

Такий трикутник можна штучно відтворити на комплексному кресленні (рис. 2.14). Горизонтальна проекція А₁В₁буде виконувати функцію катета. Другий катет, величина якого дорівнює Z_B– Z_A, будуємо, взявши за вершину прямого кута точку А₁(слід зауважити, що за вершину прямого кута може бути взятий будь який кінець проекції відрізка).

Натуральна величина відрізка прямої загального положення на комплексному кресленні будується як гіпотенуза прямокутного трикутника, перший катет якого дорівнює одній з проекцій даного відрізка, а другий - різниці відстаней від кінців відрізка, до тієї площини проекцій, на якій взято перший катет (різниці відстаней кінців другої його проекції від площини, на якій знаходиться перша проекція цього відрізка).

Кут нахилу відрізка прямої до площини проекцій визначається як кут між натуральною величиною відрізка і його проекцією на цю площину.

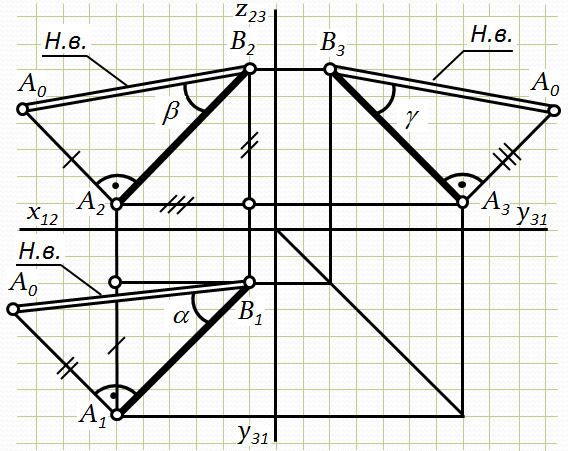Рис.2.14. Визначення натуральної величини відрізка на епюрі

Для визначення натуральної величини відрізка АВ і кута a необхідно :

1. Через одну з точок горизонтальної проекції відрізка (у нас точка А₁) провести перпендикуляр до проекції відрізка і на ньому відкласти різницю висот між точками В і А.

2. Точку А₀, яку ми отримали, з’єднуємо з точкою В₁. Відрізок А₀В₁буде натуральною величиною відрізка АВ, а кут між А₁В₁і А₀В₁буде кутом a нахилу відрізка АВ до площини проекцій П₁.

Для визначення натуральної величини відрізка АВ і кута b необхідно:

1. Через точку А₂або В₂(у нас А₂) провести перпендикуляр до А₂В₂і на ньому відкласти різницю глибин між точками А і В.

2. Точку А₀, яку ми отримали, з’єднуємо з точкою В₂. Відрізок А₀В₂буде натуральною величиною відрізка АВ, а кут між А₂В₂і А₀В₂буде кутом b нахилу відрізка АВ до площини П₂.

Для визначення натуральної величини відрізка АВ і кута нахилу його до П₃необхідно:

Через точку А₃або В₃(у нас А₃) провести перпендикуляр до А₃В₃і на ньому відкласти різницю широт між точками А і В.

2. Точку А₀, яку ми отримали, з’єднуємо з точкою В₃. Відрізок А₀В₃буде натуральною величиною відрізка АВ, а кут між А₃В₃і А₃В₃буде кутом g – кутом нахилу відрізка АВ до площини проекцій П₃.