Взаємне положення прямих

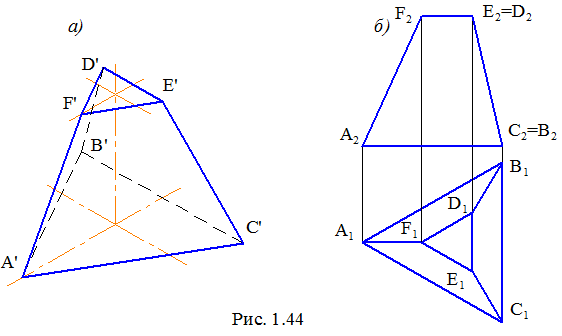Дві прямі в просторі можуть збігатися, бути паралельними, мимобіжними або перетинатися. Випадки розташування прямих розглянемо на прикладі ребер усіченої піраміди (рис. 1.44, а).

Прямі перетинаються, якщо мають одну загальну точку. Для ребер AF і FE - це вершина F. Ця точка відобразиться на кресленні проекціями, які можна з'єднати горизонтальною або вертикальною лінією зв'язку (рис. 1.44, б).

Якщо точка перетину прямих вилучена в нескінченність, прямі стають паралельними, наприклад, ребра АС і FЕ. На кресленні їхні однойменні проекції так само паралельні.

Прямі, які не паралельні між собою і не мають загальної точки, є мимобіжні. На кресленні однойменні проекції таких прямих можуть перетинатися, але точки перетину проекцій прямих не лежать на горизонтальній або вертикальній лініях зв'язку. На рис. 1.44 мимобіжними прямими є ребра АВ і ЕС.

При читанні креслення виникають завдання зворотного змісту: із наявних зображень прямих необхідно визначити їхнє взаємне положення у просторі.

Дві прямі в просторі паралельні, якщо на кресленні їхні однойменні проекції паралельні між собою. Це правило випливає із властивості паралельного проектування, поміщеного під номером 3. Кількість проекцій прямих повинно бути, як, звичайно, не менш двох. Якщо прямі паралельні якій-небудь площині проекцій, то зображення на цю площину істотно полегшує визначення їхнього взаємного положення. Аналогічний випадок був розглянутий для положення точки і прямої.

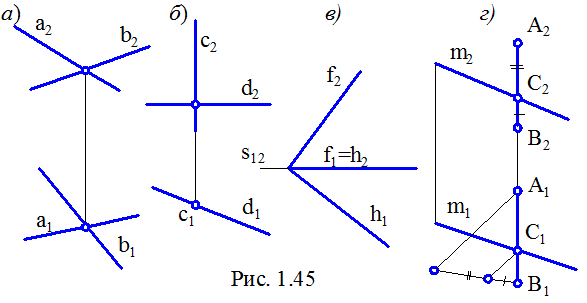Прямі в просторі перетинаються, якщо точки перетину однойменних проекцій лежать на одній лінії зв'язку. Приклади таких прямих, що займають різне положення щодо площин проекцій наведені на рис. 1.45. Оскільки одна із прямих (АВ) займає профільне положення (рис. 1.45, г), показана графічна перевірка приналежності точки перетинання з прямою АВ.

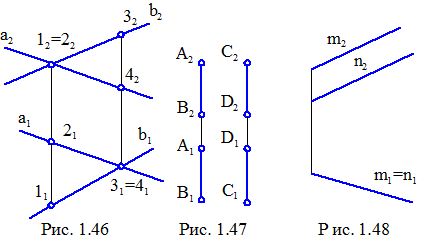Прямі в просторі мимобіжні( тобто вони не паралельніні і не перетинаються між собою), якщо точки перетину однойменних проекцій не лежать на одній лінії зв'язку(рис. 1.46).

У деяких випадках розташування прямих щодо площин проекцій, таких точок на кресленні може не бути (рис. 1.47). Це істотно ускладнює визначення взаємного положення прямих (тобто читання креслення) і може зажадати деяких додаткових побудов.

Повертаючись до креслення на рис. 1.46, розглянемо пари точок 1 і 2, 3 і 4. Виділимо їхні характерні риси. Ці пари точок належать різним прямим, але розташовуються на одному проекціюючому промені. Точки 1 і 2 розташовані на фронтально-проекціюючому промені, а 3 і 4 – на горизонтально-проекціюючому. Такі пари точок називають конкуруючими, тому що точка 1 розташовується ближче до спостерігача чим точка 2 і, тим самим, на фронтальній площині проекцій закриває останню.

Так само на горизонтальній площині проекцій точка 3 закриває точку 4 ( поняття "закриває" тут використається умовно, тому що точки не мають розмірів). За допомогою конкуруючих точок визначають видимість на кресленні.

Пересічні й паралельні прямі можуть перебувати в одній проекціюючій площині. У такому випадку їхні зображення на відповідну площину проекцій можуть збігатися (рис. 1.48). Такі прямі так само називають конкуруючими.

◊ Яке взаємне положення займають прямі на рис. 1.47?

◊ Накресліть дві прямі, що перетинаються, і проекції яких збігаються на виді справа.