Решение. Алгебраическая форма комплексного числа: .
Алгебраическая форма комплексного числа: 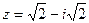 .
.
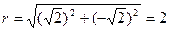 ,
, 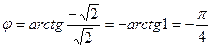 .
.
Тригонометрическая форма комплексного числа: 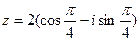 .
.
Показательная форма комплексного числа: 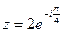 .
.
Определение 11.Уравнение 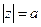 определяет на плоскости Гаусса окружность с центром в точке О и радиусом, равным а.
определяет на плоскости Гаусса окружность с центром в точке О и радиусом, равным а.
Пояснение: 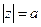
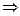
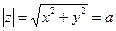
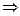
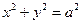 – уравнение окружности.
– уравнение окружности.
Определение 12.Уравнение 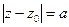 определяет на плоскости Гаусса окружность с центром в точке z0 и радиусом, равным а.
определяет на плоскости Гаусса окружность с центром в точке z0 и радиусом, равным а.
Пояснение: 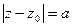
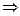
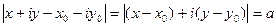
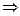
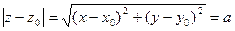
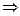
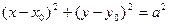 – уравнение окружности с центром в точке
– уравнение окружности с центром в точке 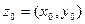 и радиусом, равным а.
и радиусом, равным а.
Замечание.Неравенство 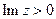 (
( 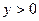 ) определяет множество точек верхней полуплоскости.
) определяет множество точек верхней полуплоскости.
Неравенство 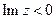 (
( 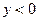 ) определяет множество точек нижней полуплоскости.
) определяет множество точек нижней полуплоскости.
Неравенство 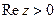 (x > 0) определяет множество точек правой полуплоскости.
(x > 0) определяет множество точек правой полуплоскости.
Неравенство 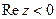 (x < 0) определяет множество точек левой полуплоскости.
(x < 0) определяет множество точек левой полуплоскости.
Пример 5. Изобразить на комплексной плоскости множество точек, задаваемых условиями 1)  , 2)
, 2)  , 3)
, 3) 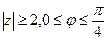 , 4)
, 4) 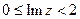 5)
5) 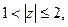
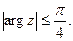
Дата добавления: 2015-07-14; просмотров: 949;
