Формы комплексного числа

Существует три формы комплексного числа, так как различные операции над комплексными числами удобнее проводить с различными формами.

1. Алгебраическая форма:z = x + iy.

Воспользуемся определением 1 и правилами (x, 0)=х, (0, y) = iy.Получим:

z = (x, y) = (x, 0) + (0, y) = x + i.

Пример 1. Найти действительную и мнимую части, модуль, аргумент комплексного числа z = 2 + 3i , сопряженное к нему и изобразить z и 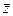на комплексной плоскости.

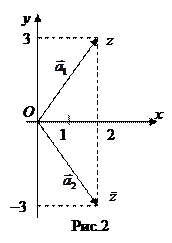Решение.

Действительная и мнимая части: Rez = x = 2, Imz = y = 3.

Модуль: .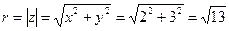

Аргумент: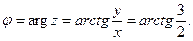

Сопряженное к z равно 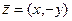, тогда, если z = 2 + 3i, то сопряженное к нему равно .

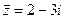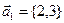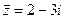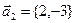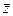Комплексному числу z = 2 + 3i соответствует вектор , комплексному числу соответствует вектор . z и изображены на рис.2.

2. Тригонометрическая форма: .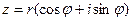

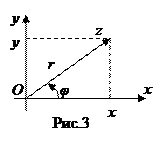Из рисунка 3 видно, что .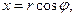

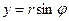Если подставить данные выражения в алгебраическую форму, то получится комплексное число в тригонометрической форме:

z = x + iy = = .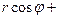

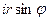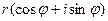Пример 2.Представить в алгебраической форме комплексное число 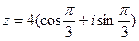. Найти к нему сопряженное.