Умножение.
Умножение производится над комплексными числами во всех формах: алгебраической, тригонометрической, показательной:
z1 · z2 = (x1 x2 – y1 y2) + i(х1 y2 + х2 y1),
z1 · z2 = 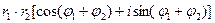
z1 · z2 = 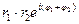
Замечание. Доказательство данных формул следует из определения мнимой единицы и правил умножения, а также тригонометрических формул.
Пример 7.Перемножить комплексные числа:
1) (1 + i) · (–2 + 3i) = (по определению) = (1· (– 2) – 1· 3) + i(1 · 3 + 1 · (–2)) = –5 + i.
(1 + i) · (–2 + 3i) = (перемножаем как многочлены) = – 2 + 3i –2i +i · 3i = –2 + i – 3= = –5 + i.
Пример 8.Получить значенияin, где n– натуральное число.
Дата добавления: 2015-07-14; просмотров: 742;
