Решение. 1. Найдем область определения: .

1. Найдем область определения: .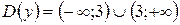

2. Исследуем функцию на четность: так как область определения функции не симметрична относительно начала координат, то данная функция не является ни четной, ни нечетной.

Исследуем функцию на периодичность: 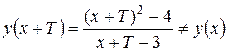ни для какого 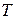, кроме 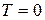, следовательно, функция не является периодической.

3. Найдем точки пересечения с осями координат:

С осью 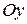: полагаем 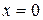, тогда 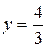, имеем точку .

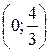С осью 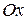: полагаем 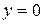, тогда 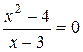, т.е. 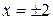, имеем точки 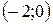и .

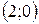Разбиваем область определения функции точками пересечения с осью на промежутки. Определим интервалы знакопостоянства функции.

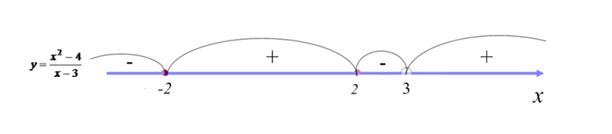
Результаты занесем в таблицу:

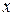
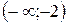
		-2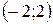
	-		+		-	+

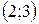
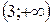
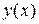
4. Точки разрыва: .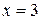

Определим поведение функции вблизи точки разрыва слева и справа: 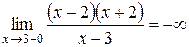и .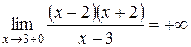

Прямая 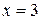- вертикальная асимптота к графику функции.

5. Исследуем поведение функции на бесконечности:

.

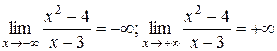6. Найдем наклонные асимптоты графика функции:

Наклонную асимптоту ищем в ви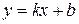де , где

, .

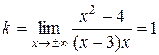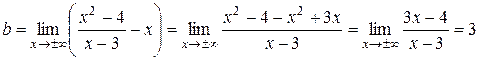Таким образом, 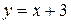- уравнение наклонной асимптоты, эта прямая проходит через точки

7. Исследуем функцию на возрастание – убывание и экстремумы.

Найдем первую производную:

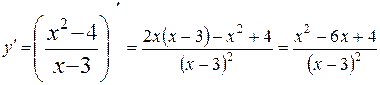
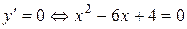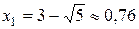
Далее ищем критические точки: так как производная данной функции существует везде в области определения функции, то критические точки определяются только из условия , 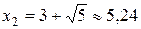- критические точки.

Критические точки разбивает область определения функции на промежутки:

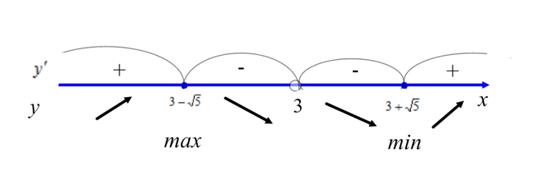
Определяем знак производной на каждом из промежутков, результаты заносим в таблицу и делаем вывод о поведении функции и существовании экстремумов.

	+		-	-		+
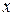
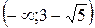
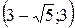
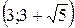
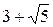
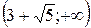
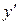
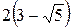
		max			min

.

.

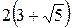
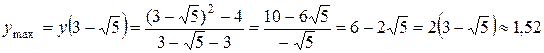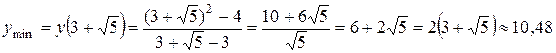8. Исследуем функцию на выпуклость-вогнутость и перегибы. Найдем вторую производную:

.

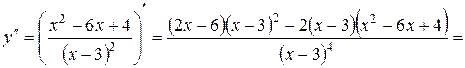
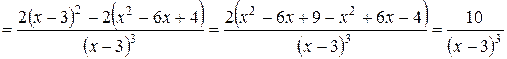Ищем точки, принадлежащие области определения, в которых 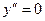или не существует.

Так как вторая производная существует везде в области определения и нигде не обращается в ноль, то определяем знак второй производной на промежутках области определения и результаты заносим в таблицу.

Делаем выводы о выпуклости-вогнутости функции. Точек перегиба функция очевидно не имеет.

	-	+

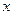
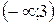
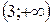
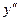
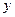
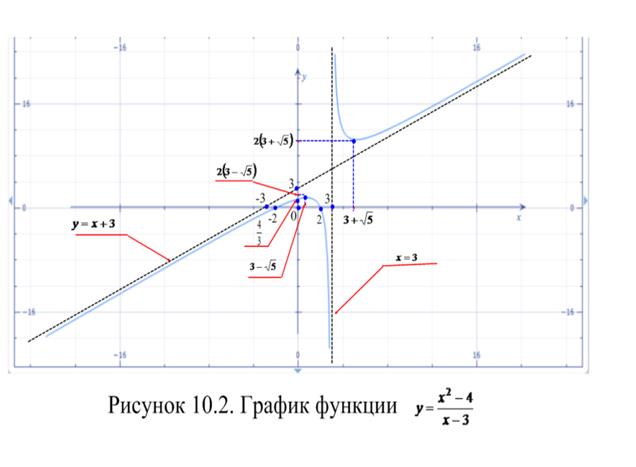
9. С помощью проведенного исследования по полученным данным строим график данной функции 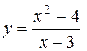(Рисунок 10.2). Для удобства изображения масштаб по осям был взят разный.

Замечание. Был указан примерный план исследования функции. Некоторые из пунктов могут быть переставлены местами, если это не противоречит логике исследования. Кроме того в отдельных случаях некоторые пункты исследования могут быть опущены (например, если при нахождении нулей функции приходится решать уравнение выше второй степени).