Порядок исследования функции на экстремум.

a. Находим область определения функции.

b. Вычисляем производную функции.

c. Определяем критические точки.

d. Область определения функции разбиваем критическими точками на промежутки и определяем знак производной на каждом полученном промежутке (с помощью метода интервалов).

e. Делаем выводы о наличие точек экстремума.

f. Вычисляем сами экстремумы функции, т.е. значения функции в точках экстремума.

Замечание. Отметим, что пункты 1-4 совпадают с порядком исследования функции на возрастание и убывание. Поэтому, исследование функции на возрастание-убывание и экстремумы рекомендуется выполнять для функции одновременно.

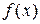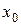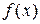Теорема (второе достаточное условие экстремума). Пусть функция имеет в точке и её окрестности непрерывные первую и вторую производные, причём , . Тогда функция имеет в точке 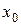минимум (максимум), если .

Доказательство.Пусть . Так как 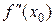непрерывна в точке 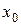, то и в некоторой окрестности точки 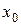. В этой окрестности точки 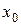функция возрастает, так как . Но . Следовательно, при переходе через точку 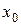в направлении возрастания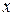 меняет знак с «-» на «+», поэтому 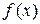имеет в точке 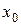минимум.

Доказательство в случае 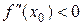аналогично.

Замечание. Второе достаточное условие имеет более узкую область применения, так как часто при и .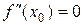

Для сформулированного достаточного условия экстремума выделим