Порядок исследования функции на возрастание и убывание.
1. Находим область определения функции.
2. Вычисляем производную функции.
3. Определяем критические точки.
4. Область определения функции разбиваем критическими точками на промежутки и определяем знак производной на каждом полученном промежутке (с помощью метода интервалов).
5. Делаем выводы о возрастании и убывании функции.
Говорят, что функция 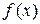 имеет в точке
имеет в точке 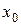 максимум (минимум), если существует такая окрестность этой точки
максимум (минимум), если существует такая окрестность этой точки 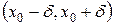 , что для всех
, что для всех 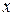 из этой окрестности, отличных от
из этой окрестности, отличных от 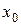 , выполняется неравенство
, выполняется неравенство 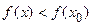
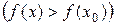 .
.
Точки максимума и минимума функции называется точками экстремума. Значения функции в точках экстремума называются экстремумами функции. По определению максимумы и минимумы функций могут достигаться лишь внутри области определения. Максимумы и минимумы в отличие от наибольшего и наименьшего значений – это локальные понятия.
Теорема (необходимое условие экстремума).Если дифференцируемая в интервале 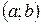 функция
функция 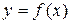 имеет в точке
имеет в точке 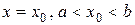 экстремум, то ее производная в этой точке равна нулю, т.е.
экстремум, то ее производная в этой точке равна нулю, т.е.  .
.
Доказательство.Предположим для определенности, что в точке 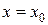 функция имеет максимум. Тогда при достаточно малых по абсолютной величине приращениях
функция имеет максимум. Тогда при достаточно малых по абсолютной величине приращениях 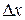
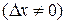 :
: 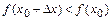 , то есть
, то есть 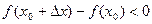 .Тогда при
.Тогда при 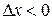
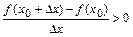 ; при
; при 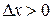
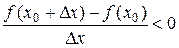 .
.
По определению производной 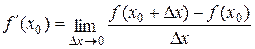 . Если
. Если 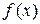 имеет производную при
имеет производную при 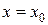 , то предел не зависит от того, как
, то предел не зависит от того, как 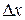 стремится к нулю. Но если
стремится к нулю. Но если 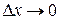 , оставаясь отрицательным, то
, оставаясь отрицательным, то 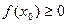 . Если
. Если 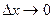 , оставаясь положительным, то
, оставаясь положительным, то 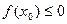 . Два последних неравенства совместимы, если
. Два последних неравенства совместимы, если 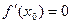 . Аналогично доказывается для минимума.
. Аналогично доказывается для минимума.
Замечание 1. Это лишь необходимое условие.
Например, для функции 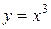
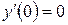 , но в точке
, но в точке 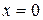 экстремума нет.
экстремума нет.
Необходимое условие экстремума позволяет выделить точки «подозрительные» на экстремум, т.е. круг точек, которые следует исследовать на экстремум с помощью достаточных условий. Точки, для которых необходимое условие не выполнено не могут быть точками экстремума.
Выделяют два достаточных условия экстремума функции, одно из них использует производную первого порядка, а второе – производную второго порядка.
Теорема (первое достаточное условие существования экстремума). Пусть функция 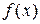 непрерывна в некотором интервале, содержащем критическую точку
непрерывна в некотором интервале, содержащем критическую точку 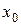 , и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки
, и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки 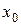 ). Если при переходе через эту точку производная меняет знак с «+» на «-» (с «-» на «+») в направлении возрастания аргумента, то функция имеет в этой точке максимум (минимум).
). Если при переходе через эту точку производная меняет знак с «+» на «-» (с «-» на «+») в направлении возрастания аргумента, то функция имеет в этой точке максимум (минимум).
Доказательство.Предположим, что производная меняет знак с «+» на «-», то есть для всех 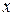 , достаточно близких к
, достаточно близких к 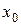 выполнены условия:
выполнены условия:
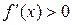 при
при 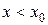 и
и 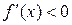 при
при 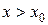 .
.
Тогда по теореме Лагранжа 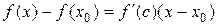 , где
, где 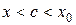 или
или 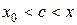 .
.
1. Пусть 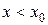 , тогда
, тогда 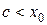 ,
, 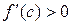 ,
,  . Следовательно,
. Следовательно, 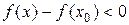 , то есть
, то есть 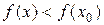 .
.
2. Пусть 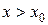 , тогда
, тогда 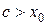 ,
, 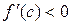 ,
,  . Следовательно,
. Следовательно, 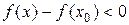 , то есть
, то есть 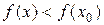 .
.
Таким образом, в обоих случаях 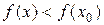 , т.е.
, т.е. 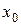 - точка максимума.
- точка максимума.
Доказательство для минимума аналогично.
Сформулированная и доказанная теорема позволяет указать
Дата добавления: 2015-08-21; просмотров: 1200;
