Порядок исследования функции на выпуклость и вогнутость, точки перегиба графика функции.

1. Находим область определения функции.

2. Вычисляем первую и вторую производные функции.

3. Определяем критические точки второго рода.

4. Область определения функции разбиваем критическими точками второго рода на промежутки и определяем знак второй производной на каждом промежутке.

5. Делаем выводы о выпуклости или вогнутости графика функции и существовании точек перегиба.

10.6

Очень часто приходится исследовать формулу кривой 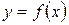, а значит, и характер изменения соответствующей функции при неограниченном возрастании абсциссы или ординаты переменной точки кривой. При этом важным частным случаем является тот, когда исследуемая кривая при удалении её переменной точки в бесконечность неограниченно приближается к некоторой прямой.

Прямая А называется асимптотой кривой, если расстояние 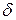от переменной точки М кривой до этой прямой при удалении точки М в бесконечность стремится к нулю.

Различают асимптоты вертикальные (параллельные оси Ox) и наклонные (не параллельные оси Ox).

Прямая 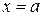называется вертикальной асимптотой графика функции 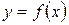, если хотя бы один из односторонних пределов 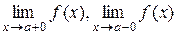является бесконечным.

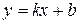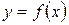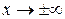Прямая называется наклонной асимптотой графика функции при , если эта функция представима в ви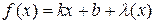де

, где .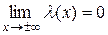

Наклонную асимптоту ищем в ви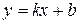де , где .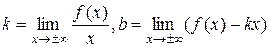

10.7

Отметим, примерный план исследования функции.

1. Находим область определения функции.

2. Исследуем функцию на четность-нечетность, периодичность.

3. Находим точки пересечения графика функции с осями координат и промежутки знакопостоянства функции.

4. Определяем точки разрыва функции и поведение функции вблизи точек разрыва. Находим вертикальные асимптоты к графику функции.

5. Выясняем поведение функции на бесконечности.

6. Находим наклонные асимптоты к графику функции.

7. Исследуем функцию на возрастание-убывание и экстремумы.

8. Выясняем вопрос о выпуклости и вогнутости графика функции, находим точки перегиба.

9. В случае необходимости находим дополнительные точки и согласно с проведённым исследованием строим график функции.

Пример. Исследовать функцию 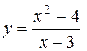и построить её график.