Лекция 9. Дифференцирование неявных и параметрически заданных функций. Логарифмическое дифференцирование. Дифференциал функции.
План лекции
9.1. Функции заданные неявно, их дифференцирование.
9.2. Параметрически заданные функции и их дифференцирование.
9.3. Логарифмическое дифференцирование.
9.4. Дифференциал функции, определение и свойства.
9.1
Пусть значения двух переменных 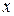 и
и  связаны между собой некоторым уравнением
связаны между собой некоторым уравнением
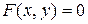 . (9.1)
. (9.1)
Если функция 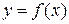 , определенная на некотором интервале
, определенная на некотором интервале 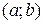 , такова, что уравнение (9.1) при подстановке в него вместо
, такова, что уравнение (9.1) при подстановке в него вместо  выражения
выражения 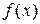 обращается в тождество относительно
обращается в тождество относительно 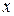 , то функция
, то функция  есть неявная функция, определенная уравнением (9.1).
есть неявная функция, определенная уравнением (9.1).
Так, например, уравнение 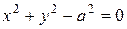 неявно определяет следующие элементарные функции:
неявно определяет следующие элементарные функции: 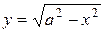 и
и 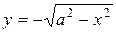 , которые определяют соответственно верхнюю и нижнюю половину окружности, радиус которой равен
, которые определяют соответственно верхнюю и нижнюю половину окружности, радиус которой равен 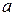 . Аналогично, уравнения
. Аналогично, уравнения 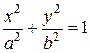 ,
, 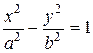 ,
,  ,
, 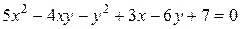 , задающие некоторые кривые второго порядка (читатель может определить вид кривой второго порядка самостоятельно), являются неявно заданными функциями.
, задающие некоторые кривые второго порядка (читатель может определить вид кривой второго порядка самостоятельно), являются неявно заданными функциями.
Но не всякую неявно заданную функцию можно представить явно в виде 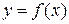 , где
, где 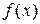 - элементарная функция. Так, например, функции
- элементарная функция. Так, например, функции 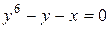 ,
,  нельзя разрешить относительно
нельзя разрешить относительно  , а уравнение
, а уравнение 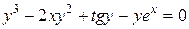 нельзя разрешить ни относительно
нельзя разрешить ни относительно 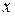 , ни относительно
, ни относительно  .
.
Поэтому необходимо указать способ отыскания производной неявно заданной функции.
Если  есть неявная функция от
есть неявная функция от 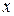 , то есть задана уравнением
, то есть задана уравнением 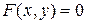 , неразрешенным относительно
, неразрешенным относительно  , то для нахождения производной
, то для нахождения производной 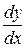 нужно продифференцировать по
нужно продифференцировать по 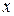 обе части равенства, помня, что
обе части равенства, помня, что  есть функция от
есть функция от 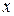 , и затем разрешить полученное равенство относительно искомой производной. Как правило, она будет зависеть от
, и затем разрешить полученное равенство относительно искомой производной. Как правило, она будет зависеть от 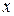 и
и  , т.е.
, т.е. 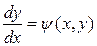 .
.
Вторую производную 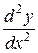 от неявной функции получаем, дифференцируя функцию
от неявной функции получаем, дифференцируя функцию 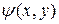 по переменной
по переменной 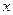 , помня, что
, помня, что 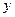 - функция от
- функция от 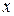
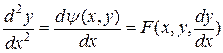 .
.
Заменяя 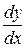 через
через 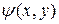 получаем
получаем 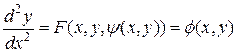 и т.д.
и т.д.
Для нахождения производных более высоких порядков этот процесс продолжаем. Для нахождения значения производной неявной функции при данном значении аргумента 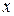 нужно знать и значение функции
нужно знать и значение функции  при данном значении
при данном значении 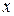 .
.
Пример 1. Найти производную функции 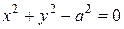 , заданной неявно.
, заданной неявно.
Решение. Дифференцируем обе части уравнения, считая  функцией аргумента
функцией аргумента 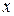 :
: 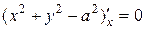 ,
, 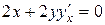 , тогда
, тогда 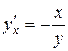 .
.
Заметим, что если бы стали дифференцировать соответствующую явную функцию 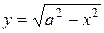 , то получили бы тот же результат:
, то получили бы тот же результат:
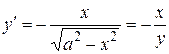 .
.
Пример 2. Найти производную второго порядка для функции 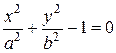 .
.
Решение. Дифференцируем по 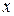 , считая
, считая 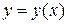 . Получаем
. Получаем 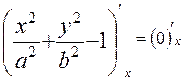 ,
, 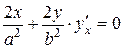 , отсюда
, отсюда 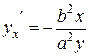 .
.
Дифференцируем вновь по 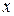 , получаем
, получаем
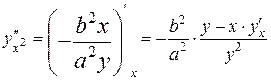 . Подставляем вместо
. Подставляем вместо  его выражение
его выражение
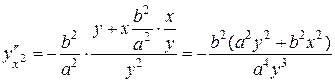 .
.
Если учесть, что из уравнения эллипса следует, что 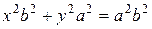 , то окончательно
, то окончательно  .
.
9.2
Если даны два уравнения
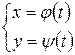 , (9.2)
, (9.2)
где 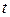 принимает значения, содержащиеся на отрезке
принимает значения, содержащиеся на отрезке  , то каждому значению
, то каждому значению 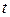 соответствуют значения
соответствуют значения 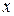 и
и  (функции
(функции  и
и 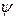 предполагаем однозначными). Если рассматривать значения
предполагаем однозначными). Если рассматривать значения 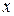 и
и  как координаты точки на координатной плоскости Оxy, то каждому значению
как координаты точки на координатной плоскости Оxy, то каждому значению 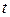 будет соответствовать определенная точка плоскости. Когда
будет соответствовать определенная точка плоскости. Когда 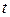 изменяется от
изменяется от 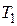 до
до  , эта точка на плоскости описывает некоторую кривую.
, эта точка на плоскости описывает некоторую кривую.
Уравнения (9.2) называются параметрическими уравнениями кривой, 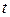 - параметром, а способ задания кривой уравнениями (9.2) – параметрическим.
- параметром, а способ задания кривой уравнениями (9.2) – параметрическим.
Предположим, что функция 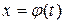 имеет обратную
имеет обратную  , тогда, очевидно,
, тогда, очевидно,  является функцией от
является функцией от 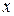 :
:
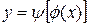 . (9.3)
. (9.3)
Таким образом, уравнения (9.2) определяют  как функцию от
как функцию от 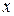 , и говорят, что функция
, и говорят, что функция  от
от 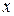 задается параметрически.
задается параметрически.
Укажем правило для вычисления производной параметрически заданной функции. Предположим, что функции 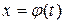 и
и 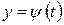 имеют производные, обратная функция
имеют производные, обратная функция  также имеет производную. Тогда определенную параметрическими уравнениями функцию
также имеет производную. Тогда определенную параметрическими уравнениями функцию 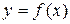 можно рассматривать как сложную функцию
можно рассматривать как сложную функцию 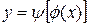 . По правилу дифференцирования сложной функции
. По правилу дифференцирования сложной функции
 (9.4)
(9.4)
На основании теоремы о дифференцировании обратной функции  . Подставляя последнее выражение в (9.4), получаем
. Подставляя последнее выражение в (9.4), получаем
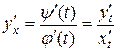 . (9.5)
. (9.5)
Выведенная формула дает возможность находить производную  от функции, заданной параметрически, не находя выражения непосредственной зависимости
от функции, заданной параметрически, не находя выражения непосредственной зависимости  от
от 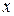 . Для нахождения второй производной
. Для нахождения второй производной  дифференцируем по
дифференцируем по 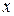 равенство (9.5), имея ввиду, что
равенство (9.5), имея ввиду, что 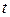 есть функция от
есть функция от 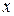 . Тогда
. Тогда 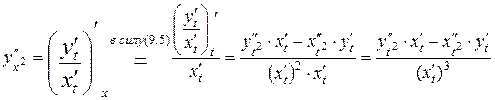 . Таким образом, получили формулу вычисления производной второго порядка для функции заданной параметрически
. Таким образом, получили формулу вычисления производной второго порядка для функции заданной параметрически
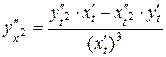 . (9.6)
. (9.6)
Пример 3. Найти производные 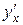 и
и 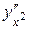 для функции, заданной параметрическими уравнениями
для функции, заданной параметрическими уравнениями 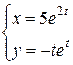 .
.
Решение. Вычисляем  ,
, 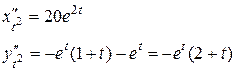 .
.
Тогда 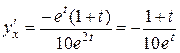 ,
,
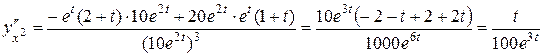 .
.
9.3
Дифференцирование многих функций значительно упрощается, если их предварительно прологарифмировать. Использование логарифмирования при нахождении производной носит название логарифмического дифференцирования. Суть его состоит в следующем.
Если требуется найти производную 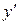 из уравнения
из уравнения 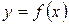 , то можно
, то можно
1. Прологарифмировать обе части уравнения 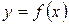 , т.е. найти
, т.е. найти 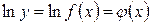 .
.
2. Найти логарифмическую производную 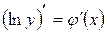 .
.
3. Записать производную искомой функции по формуле
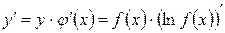 .
.
4. При необходимости провести алгебраические преобразования.
Логарифмическое дифференцирование полезно применять, когда заданная функция содержит логарифмирующиеся операции (умножение, деление, возведение в степень, извлечение корня), и в частности, для нахождения производной от показательно-степенной функции 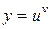 , где
, где 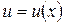 ,
, 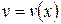 .
.
Пример 4. С помощью логарифмического дифференцирования, вычислить производную функции 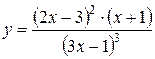 .
.
Решение. Прологарифмируем данную функцию
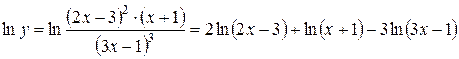 .
.
Находим логарифмическую производную
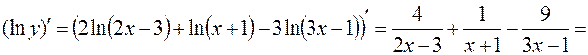
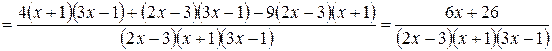 .
.
Записываем производную данной функции и проводим алгебраические преобразования
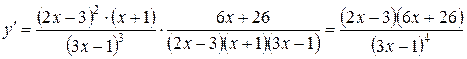 .
.
9.4
Пусть функция 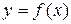 дифференцируема на отрезке
дифференцируема на отрезке 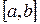 . По определению производной в некоторой точке
. По определению производной в некоторой точке 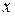 на отрезке
на отрезке 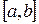 имеем
имеем 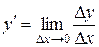 . С учетом условия существования предела
. С учетом условия существования предела
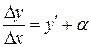 , (9.7)
, (9.7)
где 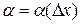 - бесконечно малая величина.
- бесконечно малая величина.
Умножим (9.7) на 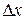
 .(9.8)
.(9.8)
Пусть 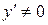 . Тогда
. Тогда 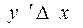 линейно по
линейно по 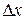 , так как
, так как 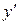 не зависит от
не зависит от 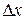 . При
. При 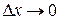 ,
, 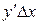 - бесконечно малая величина, но более низкого порядка чем
- бесконечно малая величина, но более низкого порядка чем 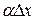 , т.к.
, т.к. 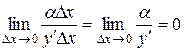 .
.
Поэтому 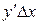 - является главной частью приращения функции, или эту величину ещё называют дифференциалом функции и обозначают
- является главной частью приращения функции, или эту величину ещё называют дифференциалом функции и обозначают  .
.
Заметим, что дифференциал функции независимой переменной, равен её приращению, т.е. 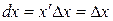 . Тогда сам дифференциал функции
. Тогда сам дифференциал функции 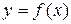 можно записать в виде
можно записать в виде 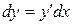 . Заметим, что отсюда и существует обозначение производной
. Заметим, что отсюда и существует обозначение производной 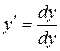 .
.
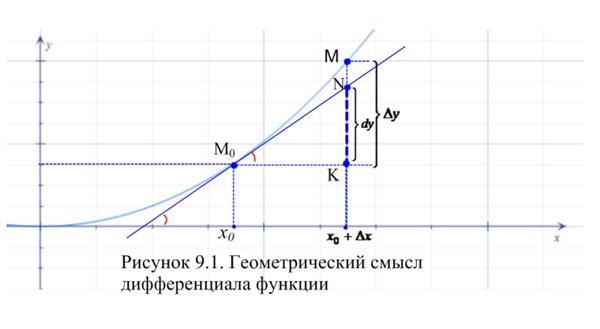
Рассмотрим геометрический смысл дифференциала функции (Рисунок 9.1). На рисунке величина отрезка 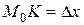 - приращение аргумента, которое придали функции в точке
- приращение аргумента, которое придали функции в точке 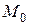 ,
, 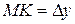 - приращение функции, вызванное приращением аргумента
- приращение функции, вызванное приращением аргумента 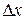 . Касательная к графику функции в точке
. Касательная к графику функции в точке 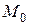 отсекает от приращения функции отрезок
отсекает от приращения функции отрезок 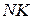 . Из прямоугольного треугольника
. Из прямоугольного треугольника 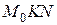 катет
катет 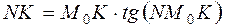 . Учитывая геометрический смысл производной,
. Учитывая геометрический смысл производной, 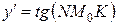 , где угол
, где угол 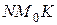 - угол наклона касательной, проведённой в точке
- угол наклона касательной, проведённой в точке 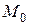 , к положительному направлению оси абсцисс. Тогда
, к положительному направлению оси абсцисс. Тогда 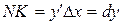 . Таким образом, с геометрической точки зрения дифференциал функции в точке – это отрезок, отсекаемый касательной от приращения функции в этой точке.
. Таким образом, с геометрической точки зрения дифференциал функции в точке – это отрезок, отсекаемый касательной от приращения функции в этой точке.
Так как 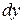 является функцией от
является функцией от 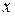 , то мы имеем право говорить о дифференциале от
, то мы имеем право говорить о дифференциале от 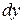 .
.
Дифференциалом второго порядка называется дифференциал от дифференциала функции, т.е. 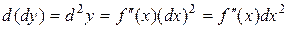 .
.
Аналогично можно дать определение дифференциала 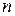 -го порядка:
-го порядка:
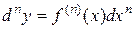 .
.
Большинство теорем и формул, относящихся к производным, сохраняют свою силу и для дифференциалов:
10 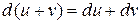 ;
;
20 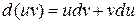 ;
;
30 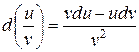 ;
;
40 Пусть 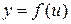 и
и 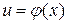 , т.е.
, т.е. 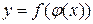 - сложная функция. По правилу дифференцирования сложной функции
- сложная функция. По правилу дифференцирования сложной функции 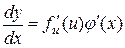 , следовательно
, следовательно 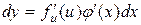 ,но
,но 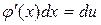 . Тогда
. Тогда 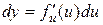 . Таким образом, форма дифференциала не зависит от того, является ли аргумент функции независимой переменной или функцией другого аргумента. Это свойство называется инвариантностью формы первого дифференциала. Заметим, что дифференциалы высших порядков таким свойством не обладают.
. Таким образом, форма дифференциала не зависит от того, является ли аргумент функции независимой переменной или функцией другого аргумента. Это свойство называется инвариантностью формы первого дифференциала. Заметим, что дифференциалы высших порядков таким свойством не обладают.
Выражение (9.8), с учетом определения дифференциала можно записать в виде 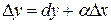 . Если
. Если 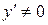 , то
, то 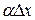 - бесконечно малая величина высшего порядка относительно
- бесконечно малая величина высшего порядка относительно 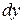 , а величины
, а величины 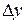 и
и 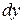 являются эквивалентными бесконечно малыми величинами при
являются эквивалентными бесконечно малыми величинами при 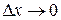
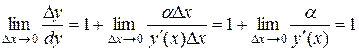 .
.
Из рисунка 9.1 видно, что чем меньше 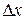 , тем меньше отличается приращение функции от дифференциала. Поэтому в приближенных вычислениях иногда пользуются приближенным равенством
, тем меньше отличается приращение функции от дифференциала. Поэтому в приближенных вычислениях иногда пользуются приближенным равенством 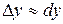 или в развернутом виде
или в развернутом виде
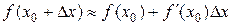 . (9.9)
. (9.9)
Формула (9.9) и носит название формулы приближённых вычислений с помощью дифференциала (в некоторых источниках – с помощью производной). Для применения этой формулы выбирают точку 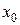 достаточно близкую к точке
достаточно близкую к точке 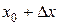 , так чтобы значение функции
, так чтобы значение функции 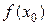 было вычислить проще, чем
было вычислить проще, чем 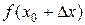 .
.
Пример5. С помощью дифференциала найдите приближенное значение 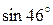 .
.
Решение. Введём функцию  . Учитывая, что
. Учитывая, что 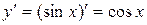 , то получаем формулу приближённого вычисления
, то получаем формулу приближённого вычисления 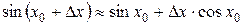 . Переводя градусы в радианы, получаем
. Переводя градусы в радианы, получаем
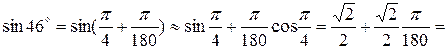
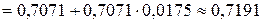 .
.
Дата добавления: 2015-08-21; просмотров: 5379;
