Рішення
На першому етапі рішення задачі застосовується до функції Т(х,t) пряме перетворення Фур'є по перемінній х
T(x,t) ®F(s,t)=  (4)
(4)
де T(x,t) – оригінал (шукана функція); F(s,t) зображення для функції
T(-¥ < s< + ¥ - деякий параметр).
Метою даного етапу є перебування зображення F(s,t) за допомогою перетвореної системи рівнянь (1) – (2) відповідно до формули (4). Використовуючи формули, аналогічні (4), одержуємо для лівої і правої частин рівняння (1), а також початкової умови (2) наступні перетворення Фур'є
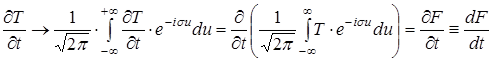 , (5)
, (5)

 (6)
(6)
Застосовуючи до інтегралу, що розміщений в правій частині (6), двічі метод інтегрування по частинам і враховуючи граничні умови (3), одержуємо, що
 (7)
(7)
Тоді
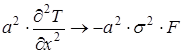 (8)
(8)
Для початкової умови (2) маємо
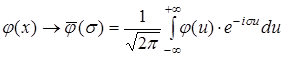 (9)
(9)
Таким чином, враховуючи (5) - (9) для знаходження зображення F(s,t) одержуємо звичайне диференціальне рівняння 1-го порядку з розподілювальними перемінними (замість диференціального рівняння в частинних похідних 2-го порядку для функції Т(х,t)
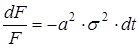 (10)
(10)
з початковою умовою
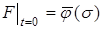 (11)
(11)
Рішення рівняння (10) з урахуванням (11) одержуємо прямим інтегруванням лівої і правої його частин
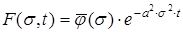 (12)
(12)
На другому етапі рішення задачі для знаходження шуканого рішення Т(х,t) використовується зворотне перетворення Фур'є
 (13)
(13)
Підставляючи (12) у (13), одержуємо
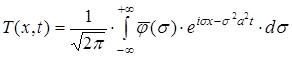 (14)
(14)
З урахуванням (9) для визначення T(x,t) одержуємо наступний подвійний інтеграл

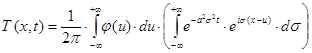 (15)
(15)
|
Для обчислення внутрішнього інтеграла I скористаємося відомою формулою Ейлера
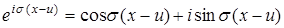 (16)
(16)
Одержуємо

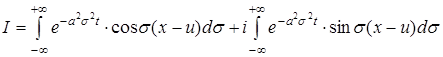 (17)
(17)
|
Враховуючи, що I¢ = 0 (інтеграл від непарної функції із симетричними межами), маємо
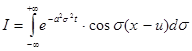 (18)
(18)
Вираз для інтегралів типу (18) можна знайти в спеціальних довідниках[1]
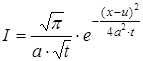 (19)
(19)
Підставляючи (19) у (15), одержуємо наступне рішення вихідної задачі
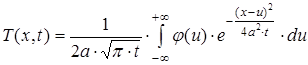 (20)
(20)
Як приклад використання формули (20) розглянемо окремий випадок із заданою функцією j(х) у вигляді деякого прямокутного імпульсу

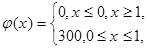 (21)
(21)
де х – у м, j(х)- у °С.
Підставляючи (21) у (20), маємо
 (22)
(22)
Зведемо інтеграл, що розміщений в правій частині (18), до спеціальної функції (інтеграл помилок, інтеграл Лапласа, інтеграл імовірностей)
erf(z) =  , (23)
, (23)
значення якої для різних значень аргументу z можна знайти в довідковій літературі. Для цього зробимо заміну перемінних в інтегралі (23)
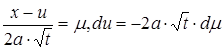 (24)
(24)
Одержуємо

 (25)
(25)
З урахуванням (23) одержуємо наступну формулу для розподілу температури в розглянутому середовищі в будь-який момент часу
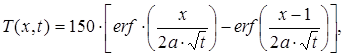 (26)
(26)
де Т - у °С; t- у с.
Задача 2 Процес нагрівання виробу рухливим джерелом теплового впливу описується наступним рівнянням теплопровідності (рис.3, рухлива система координат).
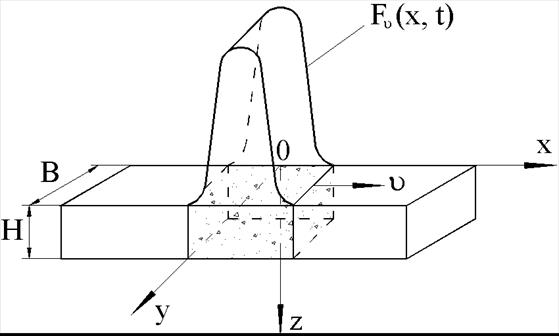
Рисунок 3 – Схема теплової дії на виріб ( 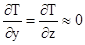 - вузький тонкоплівочний елемент, тонкий, довгий стрижень та інше)
- вузький тонкоплівочний елемент, тонкий, довгий стрижень та інше)
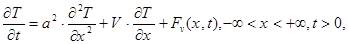 (27)
(27)
початковою умовою
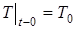 (28)
(28)
і граничними умовами
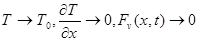 при х®±¥, (29)
при х®±¥, (29)
де V - швидкість руху джерела; Fv(x,t) - об'ємна густина теплового потоку;
Т0 = const - початкова температура виробу. Потрібно, використовуючи метод інтегральних перетворень Фур'є, знайти загальне рішення задачі T(x,t).
Рішення.
Шляхом відповідної заміни перемінних перетворимо систему рівнянь
(27) – (29) до стандартного (фундаментального) виду, а потім для рішення отриманих рівнянь використаємо метод інтегральних перетворень Фур'є. Спочатку зробимо заміну
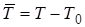 (30)
(30)
Одержуємо
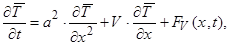 (31)
(31)
 (32)
(32)
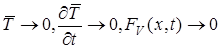 при х ®±¥ (33)
при х ®±¥ (33)
Далі виключимо з рівняння (31) член 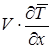 , зробивши заміну перемінних
, зробивши заміну перемінних
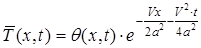 (34)
(34)
Підставляючи (34) у (31) - (33), одержуємо для функції 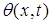 уже фундаментальну систему рівнянь
уже фундаментальну систему рівнянь
|
 (35)
(35)
|
 при х ® ±¥, (37)
при х ® ±¥, (37)
Як і при рішенні першої задачі, для знаходження функції 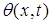 на 1-муетапі використовуємо пряме перетворення Фур'є по координаті х
на 1-муетапі використовуємо пряме перетворення Фур'є по координаті х
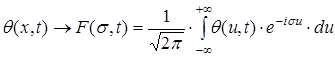 (39)
(39)
Також як і при рішенні попередньої задачі, знайдемо F( 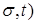 , перетворивши (35) - (37) відповідно до (39)
, перетворивши (35) - (37) відповідно до (39)
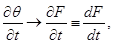 (40)
(40)
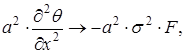 (41)
(41)
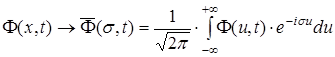 (42)
(42)
Використовуючи (40)-(42), для знаходження F(s,t) одержуємо звичайне лінійне диференціальне рівняння 1-го порядку, яке уже можна вирішити одним із стандартних методів (наприклад, методами Бернуллі, Ейлера та ін.)
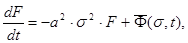 (43)
(43)
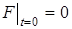 (44)
(44)
Знайдемо рішення (43) - (44) методом Бернуллі
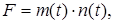 (45)
(45)
де m(t) і n(t) – дві невідомі функції, що знаходяться в процесі рішення
(43) – (44). Підставляючи (45) у (43), одержуємо
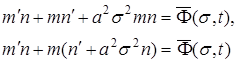 (46)
(46)
Функцію n(t) знаходимо, спростивши (46)
 (47)
(47)
Інтегруючи (47), (константу в рішенні опускаємо) одержуємо
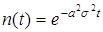 (48)
(48)
З урахуванням (46) і (48) знаходимо
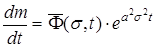 (49)
(49)
Звідси
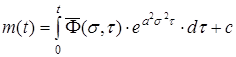 , (50)
, (50)
де с – деяка постійна. Підставляючи (48) і (50) у (45), одержуємо
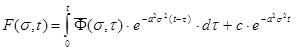 (51)
(51)
З урахуванням початкової умови (44), остаточно, для F(s,t) одержуємо наступний вираз
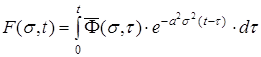 (52)
(52)
На другому етапі рішення задачі для знаходження оригіналу 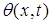 скористаємося зворотним перетворенням Фур'є для функції F(s,t)
скористаємося зворотним перетворенням Фур'є для функції F(s,t)
 (53)
(53)
Підставляючи (42) і (52) у (53), одержуємо
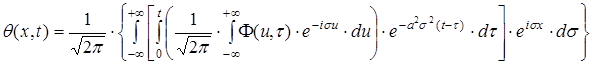 (54)
(54)
Згрупувавши інтеграли в (54) і розбивши їх на внутрішній і зовнішній, знаходимо

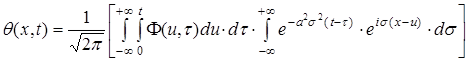 (55)
(55)
|
Також як і в попередній задачі, для знаходження внутрішнього інтеграла 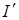 використовується (16) і довідкова література
використовується (16) і довідкова література
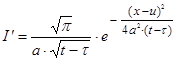 (56)
(56)
Підставляючи (56) у (55), одержуємо наступне рішення для функції 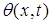
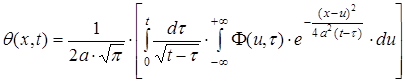 (57)
(57)
Використовуючи (30), (34) і (57), остаточно, для рішення вихідної задачі маємо

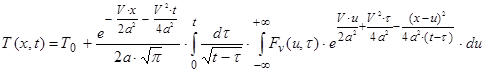 (58)
(58)
Розглянемо джерело теплового впливу з нормально розподіленою потужністю (гаусового типу)
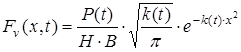 , (59)
, (59)
де Р(t) – потужність джерела в центрі впливу; k(t) коефіцієнт зосередженості джерела; Н, В – відповідно товщина і ширина елемента. Підставляючи (59) у (58) і враховуючи що Р(t) =Р0 і k(t) =k0 (Р0 і k0 - постійні величини), одержуємо
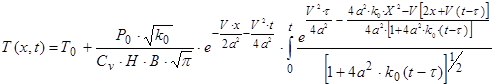 (60)
(60)
Формула (60) дозволяє проводити розрахунки розподілів температури в різних тонкоплівкових виробах машинобудування, точного приладобудування, космічної й авіаційної техніки та ін. при їхній обробці рухливими концентрованими джерелами тепла (різець, фреза, електронний промінь, лазерне випромінювання та ін).
Дата добавления: 2015-08-21; просмотров: 681;
