Загальні принципи методу розділення перемінних

Метод розділення перемінних є одним з фундаментальних аналітичних методів рішення всіляких задач теплопровідності для обмежених середовищ (пластини кінцевої товщини, тонкі стержні та ін.).

Метод розділення перемінних - при розв’язуванні задач теплопереносу застосовується коли:

1. Рівняння теплопровідності для функції T(x,t) є лінійним і однорідним (не обов'язково з постійними коефіцієнтами), тобто

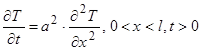(1)

2.

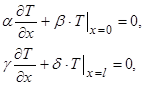
де a, b, g, d - константи (граничні умови, задані в такому вигляді, називаються лінійними однорідними граничними умовами).

Для розуміння методу розберемо спочатку часткову задачу (Рис.1).

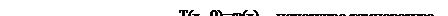
Розглянемо задачу теплопровідності: знайти розв’язок рівняння (1), що задовольняє граничним умовам

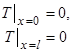
і початковій умові

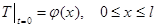(6)

Перш ніж приступити до розподілу перемінних, дамо фізичну інтерпретацію нашої задачі. Отже, мається стержень кінцевої довжини, кінці якого підтримуються при постійній, рівний нулю температурі (насправді кінці можуть підтримуватися при набагато більш високій температурі, значення якої приймається за початок відліку). Додаткові дані про задачу представлені у вигляді початкової умови.

Наша мета – знайти розподіл температури T(x,t) у наступні моменти часу. Для найпростішого рівняння з частковими похідними типу (1) поділ змінних – це пошук рішень вигляду

T(x,t)=M(x)×N(t), (7)

де М(х) – функція, що залежить тільки від перемінної х, а N(t) - залежна тільки від t. Таке рішення є в якомусь змісті найпростішим, оскільки температура T(x,t), представлена в такому вигляді, буде зберігати «форму» профілю в різні моменти часу t (Рис.2).

Загальна ідея полягає в тому, щоб знайти нескінченне число таких розв’язків рівняння з частковими похідними (1) (які задовольняють граничним умовам). Ці найпростіші функції T_n(x,t) = M_n(x)×N_n(t) (названі фундаментальними розв’язками) є як би елементарними цеглинками, з яких будується розв’язок вихідної задачі. Розв’язок вихідної задачі T(x,t) знаходяться у вигляді такої лінійної комбінації фундаментальних розв’язків Mn(x)×Nn(t), що результуюча сума

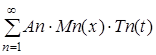(8)

задовольняє початковим умовам. Оскільки ця сума задовольняє рівнянню і граничним умовам, вона є розв’язком вихідної задачі. Тепер проробимо всі ці викладення докладно.