Розв‘язок задач теплопровідності для напівобмежених середовищ

Задачі теплопереносу в напівобмежених середовищах необхідні для оцінки теплових полів по глибині матеріалів при їхній поверхневій обробці різними фізико-технічними методами. До числа типових задач відносяться, наприклад, задачі нагрівання матеріалів для випадків, коли на оброблюваній поверхні підтримується задана температура (граничні умови I роду) чи заданий тепловий потік (граничні умови II роду), а також задачі конвективного охолодження в зонах впливу різних джерел тепла (граничні умови III роду). Крім цього, для більшості практичних розрахунків, як правило, використовуються одномірні, нестаціонарні рівняння теплопровідності.

Використовуємо метод інтегральних перетворень Фур'є для розв’язку такого типу задач.

Задача 3. Процес обробки виробу здійснюється таким чином, що температура оброблюваної поверхні залежить тільки від часу і дорівнює Т_п (t). При цьому теплоперенос у виробі описується наступним рівнянням теплопровідності з граничною умовою на поверхні I роду (Рис. 3)

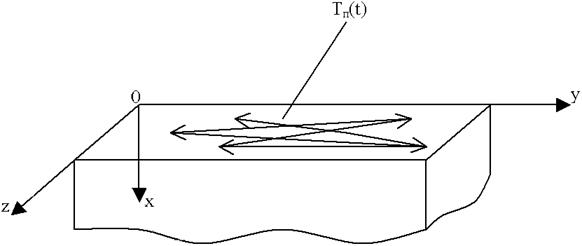
Рисунок 3 – Схема теплового впливу на оброблювані вироби

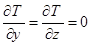( - напівобмежені, невеликих поперечних розмірів бруски, стержні, шайби та інші тіла при їх багатоцільовій (скануючій) торцевій (поверхня oyz) обробці рухомим джерелом теплової дії):

® - можливі напрямки змінного руху джерела тепла

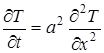, 0 < x < +¥, t > 0 (1)

з початковою умовою

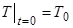(2)

і граничними умовами

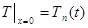(3)

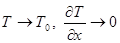при х ® +¥, (4)

де Т₀ =const – початкова температура виробу.

Потрібно, використовуючи метод інтегральних перетворень Фур'є, знайти загальний розв’язок задачі T(x,t).