Розглянемо типову теплову задачу

(39)

(40)

(41)

(42)

Для того, щоб перетворити ці граничні умови в нульові (після деяких проб і помилок) зупинилися на наступній формі розв’язку:

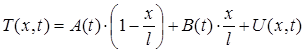, (43)

де функції A(t) і B(t) вибираються так, щоб “квазістаціонарна” частина розв’язку (43)

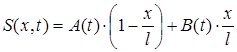(44)

задовольняла граничним умовам вихідної задачі. У цьому випадку функція U(x,t) буде задовольняти однорідним граничним умовам. Підставляючи функції S(x,t) у граничні умови

(45) – (46)

одержуємо два рівняння, з яких можна визначити А(t) і В(t). У результаті одержуємо

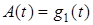, (47)

(48)

Отже

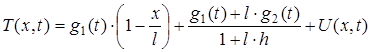(49)

Якщо підставити цей вираз для T(x,t) у вихідну задачу (39) –(42), ми одержимо нову задачу для невідомої функції U(x, t):

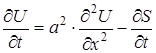- (неоднорідне рівняння теплопровідності), (50)

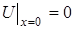, (51)

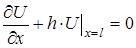- (однорідні граничні умови), (52)

(нова початкова умова з відомою функцією). (53)

Тепер перед нами нова задача з однорідними граничними умовами (на жаль, розв’язок став неоднорідним). Цю задачу не можна вирішити методом розділення перемінних, але вона легко вирішується розглянутим у попередніх лекціях методом інтегральних перетворень Фур'є.

Література, яка рекомендується для вивчення дисципліни

1. Лыков А.В. Теория теплопроводности. – М.:Высшая школа, 1967.

2. Тихонов А.М., Самарский А.А. Уравнения математической физики. – М.:Наука, 1966.

3. Беляев Н.М., Рядно А.А. Методы теории теплопроводности. – М.:Высшая школа, 1982.

4. Резников А.Н., Резников Л.А. Тепловые процессы в технологических системах. – М.:Машиностроение, 1990.

5. Калиниченко В.И. и др. Численные решения задач теплопроводности. – Харьков: Вища школа, 1993.

6. Ящерицын П.И. и др. Теория резания. Физические и тепловые процессы в технологических системах. – М.:Высшая школа, 1990.

7. Попов С.А. и др. Алмазно-абразивная обработка металлов и твердых сплавов. – М.:Машиностроение, 1974.

8. Лазерная и электронно-лучевая обработка материалов. Справочник //Н.Н.Рыкалин и др. – М.:Машиностроение, 1985.

Додаткова література

9. Лыков А.В., Михайлов Ю.А. Теория тепло- и массопереноса. – М.:Госэнергоатомиздат, 1963.

10. Карслоу Г., Егер Д. Теплопроводность твердых тел. – М.:Наука, 1964.

11. Бицадзе А.В. Уравнения математической физики. – М.:Наука, 1982.

12. Маслов В.П., Данилов В.Г., Волосов К.А. Математическое моделирование процессов тепло-массопереноса. – М.:Наука, 1976.

13. Углов А.А. Математическое моделирование процессов тепло-массопереноса. – М.:Наука, 1976.

14. Физико-химические процессы обработки материалов концентрированными потоками энергии /С.И.Анисимов и др. – М.:Наука, 1989.

[1] Например: Справочник по специальным функциям с формулами, графиками и математическими таблицами. /Под ред. М.Абрамовица и И. Стиган- М.: Наука, 1979, 832 с

[2] В протилежному випадку рівняння М^² - k×M = 0 з граничними умовами М(0) = М(l) = 0 має тільки тривіальне рішення М(х) @ 0

[3] Відзначимо, що функції T_n і T_-n відрізняються тільки знаком