Поняття про редукційну задачу

Результати геодезичних вимірювань, які виконуються на земній поверхні, відносяться до різних рівневих поверхонь. Це ж саме відноситься і до результатів астрономічних спостережень. Для визначення взаємного положення пунктів в єдиній системі координат за результатами геодезичних і астрономічних вимірів останні повинні бути приведені до однієї рівневої поверхні або взагалі до однієї, певним чином встановленої, відлікової поверхні.

Віднесення результатів астрономічних спостережень і геодезичних вимірювань до поверхні геоїда полягає, в основному, у введенні поправок за висоту пунктів над рівнем Світового океану. Оскільки поверхня геоїда має досить складну форму, а її розміри не відомі, то при математичному опрацюванні результатів геодезичних вимірювань поверхня геоїда замінюється більш простою геометричною відліковою поверхнею – земним еліпсоїдом. Розміри земного еліпсоїда і його положення або орієнтування в тілі Землі повинні бути встановлені так, щоб його поверхня була близькою до поверхні геоїда.

У класичному методі визначення геодезичних координат треба здійснити перехід від довжин ліній і горизонтальних напрямів, виміряних на фізичній поверхні Землі, до довжин відповідних геодезичних ліній і до напрямів цих ліній на референц-еліпсоїді. Виникає так звана редукційна задача вищої геодезії.

Редукційною задачею називають теорію переходу від безпосередньо виміряних на фізичній поверхні Землі величин (довжин ліній, горизонтальних напрямів та вертикальних кутів, прискорень сили ваги) до відповідних їм величин на поверхні прийнятого еліпсоїда.

У класичній геодезії обчислення планових координат - геодезичної широти і -геодезичної 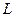довготи пунктів прийнято виконувати окремо від геодезичних висот 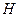. Подальше опрацювання геодезичної мережі ведеться на поверхні земного еліпсоїда і є, фактично, розв’язком двовимірної задачі. При цьому можна, в залежності від практичної необхідності, виконати проектування елементів мережі вже з поверхні еліпсоїда на сферу або площину.

Технологія обчислення геодезичних широт і довгот передбачає проектування пунктів тріангуляції з фізичної поверхні Землі на поверхню земного еліпсоїда, переважно, на референц-еліпсоїд. Проекції цих пунктів утворюють ряд точок на поверхні референц-еліпсоїда, що з'єднуються геодезичними лініями. В результаті цього отримують мережу, що складається із сфероїдних трикутників. Із розв'язування цих трикутників визначають довжини їх сторін (довжини геодезичних ліній), а в подальшому, шляхом розв’язування головних геодезичних задач від вихідного пункта мережі, використовуючи при цьому виміряні горизонтальні напрями, знаходять геодезичні координати 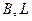решти пунктів та геодезичні азимути для всіх можливих напрямів.

Існує два методи розв’язання редукційної задачі: математично строгий метод - метод проектування, і наближений - метод розгортання.

Для застосування методу проектування вже повинна бути з достатньою точністю відома фігура Землі. А саме, потрібно знати:

• з похибкою декількох мінут геодезичні координати 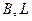пунктів та геодезичні азимути напрямів;
• з похибкою 1-3 м, а в деяких випадках і точніше, геодезичні висоти пунктів ;
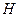• з похибкою 1-2 " складові відхилення прямовисної ліні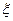ї і .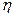

Наближені значення геодезичних координат 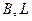, які необхідні для редукування тріангуляції, можна зняти з топографічної карти або обчислити шляхом розв’язування прямих геодезичних задач на поверхні еліпсоїда, використовуючи при цьому виміряні (не редуковані) горизонтальні напрями.

Геодезичну висоту 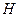представляють у вигляді суми 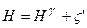, де 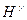- нормальна висота, що визначається з високою точністю із геометричного нівелювання, - висота квазігеоїда над референц-еліпсоїдом. Останні висоти визначають із астрономічного чи астрономо-гравіметричного нівелювання.

Складові відхилення прямовисних ліній 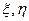безпосередньо можуть бути обчислені тільки для тих пунктів, де виконані астрономічні визначення широт і довгот. Для решти пунктів їх отримують методом непрямої інтерполяції з використанням гравіметричних даних.

При початковому опрацюванні тріангуляції перерахованих вище даних, необхідних для проведення редукування, ще немає. Можна отримати тільки висоти пунктів над геоїдом (квазігеоїдом) із геометричного нівелювання та обчислити наближені значення координат 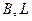і азимутів напрямів . З цими даними для редукування результатів геодезичних вимірювань на поверхню референц-еліпсоїда використовується метод розгортання.

При застосуванні методу розгортання геодезичну мережу фактично редукують прямовисними лініями на геоїд, використовуючи для лінійних редукцій висоти над рівнем моря, але вважають, що тим самим виконано редукування на референц-еліпсоїд. Метод розгортання можна трактувати як наближений метод проектування, коли при обчисленні редукцій не акцентується на різниці між геоїдом і референц-еліпсоїдом, а прямовисні лінії розглядаються як нормалі до референц-еліпсоїда. Звісно, різниці між поверхнями референц-еліпсоїда і геоїда будуть відносно малими за величиною лише у тому випадку, коли розміри і орієнтування референц-еліпсоїда визначені під умовою якнайбільшої близькості його поверхні до поверхні геоїда. Проте навіть тоді не можна не рахуватися з впливом відступів геоїда на результати опрацювання геодезичних вимірів.

Впливи відступів геоїда від прийнятого референц-еліпсоїда на результати геодезичних визначень можуть бути усунуті тільки застосуванням відповідних способів приведення геодезичних вимірів до поверхні референц-еліпсоїда. Математично однозначне визначення положення пунктів на поверхні референц-еліпсоїда може бути досягнуто тільки при проектуванні їх на цю поверхню нормалями до неї. Отже, правильне опрацювання геодезичних вимірювань, пов’язане з введенням у них редукцій - поправок, що однозначно визначаються відповідними відступами поверхні геоїда від прийнятого референц-еліпсоїда.

З теоретичних позицій для застосування вказаного методу проектування можна прийняти будь-який референц-еліпсоїд, який характеризує фігуру Землі, в тому числі і загальний земний еліпсоїд. Якщо знати відступи геоїда від прийнятого еліпсоїда, то завжди можна достатньо точно визначити ті поправки, які повинні бути введені у результати геодезичних вимірювань для віднесення їх до поверхні цього еліпсоїда. Проте, якщо відступи геоїда будуть досить значними, то відповідні їм редукції геодезичних вимірювань також будуть значними. В цьому випадку результати вимірів, особливо лінійних, після приведення їх до поверхні еліпсоїда будуть дуже відрізнятися від їх значень, отриманих на поверхні геоїда. З чисто практичних потреб їх використання необхідно, щоб вони не підлягали великим спотворенням, хоча і досить закономірним у математичному плані. Тому при опрацюванні геодезичних вимірювань методом проектування також необхідно застосовувати такий еліпсоїд, який за розмірами та орієнтуванням найбільш близько підходить до фігури геоїда на конкретній ділянці Землі, тобто референц-еліпсоїд.

Розглянемо формули, за якими обчислюють поправки в лінійні вимірювання (вимірювання відстаней між пунктами мережі світло- або радіовіддалемірами чи GPS-методами ) та кутові вимірювання (горизонтальні напрями) для редукування їх на референц-еліпсоїд методом проектування.