Динамічні висоти

Система ортометричних висот, як і система нормальних висот мають спільний недолік, а саме, рівнева поверхня у загальному випадку буде мати різні висоти, оскільки будуть різними в різних точках даної рівневої поверхні чи різною буде нормальна сила ваги (залежить від широти). Цей недолік ортометричних і, в деякій мірі, нормальних висот, що є значною перешкодою при використанні висот в інженерних задачах, і особливо задачах гідротехнічного характеру, усувається введенням так званих динамічних висот, тобто введенням такої системи висот, в якій висота всіх точок одної і тої ж рівневої поверхні буде постійною. Порівнюючи вирази (5.32) і (5.34), можна побачити, що інтегральний множник у них однаковий і повністю характеризує положення точки по висоті, оскільки числова величина інтегралу 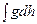в будь-якій точці одної і тої ж рівневої поверхні є постійною. Змінними величинами у формулах (5.32) і (5.34) є і . Тому, якщо замінити їх на якесь фіксоване значення сили ваги, то тоді указані формули будуть виразом динамічної висоти, яка при переміщенні точки по рівневій поверхні не змінюється.

Позначивши динамічну висоту через 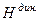та прийнявши за фіксоване значення нормальної сили ваги на широті 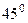- 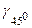, будемо мати

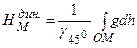. (5.41)

Динамічні висоти, як і геопотенціальні величини, однакові для всіх точок одної рівневої поверхні; вони не залежать від шляху нівелювання. За фіксоване значення сили ваги не обов’язково приймати 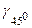; можна взяти, наприклад, середнє значення сили ваги для даного району. Такі висоти будуть володіти також всіма властивостями динамічних висот.

Формула динамічної висоти (5.41), у результаті перетворення, аналогічного до попередніх, приводиться до вигляду

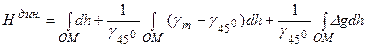.(5.42)

Динамічні висоти не знайшли застосування в питаннях, що пов’язані з дослідженням та визначенням фігури Землі, за винятком окремих випадків інженерної практики, де суттєвою є умова сталості висот однієї рівневої поверхні.

5.5. Редукування геодезичних вимірювань з фізичної поверхні на поверхню земного еліпсоїда