Нормальні висоти
Ортометричні висоти мають суттєвий недолік принципового характеру – вони не можуть бути обчислені точно, оскільки при цьому, як вже вище зазначалося, необхідно задаватися тією чи іншою моделлю розподілу мас в тілі Землі. Від цього недоліку ортометричних висот вільні нормальні висоти, які ввів Молоденський при розробці загальної теорії фігури Землі [11].
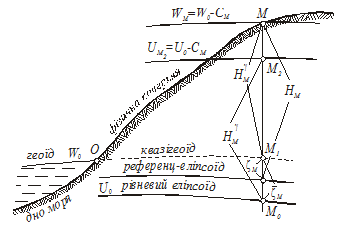
Нормальною висотою НgМ точки М фізичної поверхні Землі (рис.5.3) називається відрізок М0М2 силової лінії, що проходить через точку 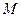 в полі нормального потенціалу сили ваги, між рівневими поверхнями
в полі нормального потенціалу сили ваги, між рівневими поверхнями 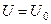 (рівневий еліпсоїд) і
(рівневий еліпсоїд) і 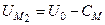 .
.
|
Рис. 5.3
Числове значення нормальної висоти одержують за формулою
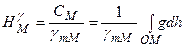 , (5.34)
, (5.34)
де 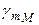 – середнє значення нормальної сили ваги по лінії М0М2. За аналогією з отриманням виразу (5.33), формулу (5.34) можна перетворити
– середнє значення нормальної сили ваги по лінії М0М2. За аналогією з отриманням виразу (5.33), формулу (5.34) можна перетворити
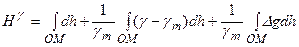 . (5.35)
. (5.35)
З формули видно, що перший член представляє суму виміряних перевищень в нівелірному ході, другий член є поправкою за непаралельність рівневих поверхонь нормального поля сили ваги, а останній член – це поправка за відхилення дійсного гравітаційного поля Землі від нормального.
Якщо від точок фізичної поверхні Землі відкласти по силових лініях нормального гравітаційного поля вниз їх нормальні висоти, то отримаємо поверхню квазігеоїда. Тоді нормальну висоту можна розглядати як висоту точки фізичної поверхні Землі над квазігеоїдом.
Геодезична висота 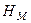 точки
точки 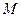 дорівнює сумі нормальної висоти
дорівнює сумі нормальної висоти 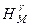 і аномалії висоти
і аномалії висоти 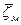 . Аномалія висоти
. Аномалія висоти 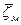 дорівнює відрізку
дорівнює відрізку 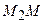 і називається висотою квазігеоїда над відліковою поверхнею (див. рис. 5.3). Суттєвих поправок за те, що геодезичні висоти відкладають не по силових лініях нормального поля, а по нормалях до еліпсоїда, не виникає. Якщо відліковою поверхнею є референц-еліпсоїд, то
і називається висотою квазігеоїда над відліковою поверхнею (див. рис. 5.3). Суттєвих поправок за те, що геодезичні висоти відкладають не по силових лініях нормального поля, а по нормалях до еліпсоїда, не виникає. Якщо відліковою поверхнею є референц-еліпсоїд, то
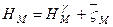 , (5.36)
, (5.36)
а якщо рівневий еліпсоїд нормального поля, то
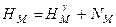 . (5.37)
. (5.37)
Висоти 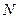 визначають за допомогою глобальних гравітаційних моделей Землі, висоти (аномалії висот) `z - методом астрономічного чи астрономо-гравіметричного нівелювання.
визначають за допомогою глобальних гравітаційних моделей Землі, висоти (аномалії висот) `z - методом астрономічного чи астрономо-гравіметричного нівелювання.
Перевагою нормальних висот над ортометричними є те, що вони відповідають такому поділу геодезичної висоти H на гіпсометричну і геоїдальну складові, при якому кожна з них може бути однозначно і строго визначена лише за вимірами на фізичній поверхні Землі.
Порівнюючи формули (5.33) і (5.35), можна побачити, що ортометричні висоти відрізняються від нормальних на величину
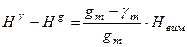 , (5.38)
, (5.38)
яка визначається наближено. Ця величина якраз характеризує відступи квазігеоїда від геоїда. Якщо приймемо 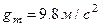 ,
, 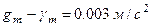 та
та 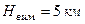 , то різниця
, то різниця 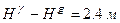 ; для більш рівнинних районів при
; для більш рівнинних районів при 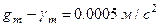 та
та 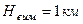 різниця буде біля
різниця буде біля 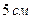 . З аналізу виразу (5.38) можна зробити висновок, що квазігеоїд співпадає з геоїдом, коли
. З аналізу виразу (5.38) можна зробити висновок, що квазігеоїд співпадає з геоїдом, коли 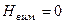 або
або 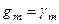 . Це означає співпадання ортометричних і нормальних висот на рівні моря, а також в точках земної поверхні, де
. Це означає співпадання ортометричних і нормальних висот на рівні моря, а також в точках земної поверхні, де 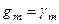 .
.
Якщо ходом нівелювання є замкнутий полігон 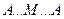 , то повинна виконуватися рівність
, то повинна виконуватися рівність
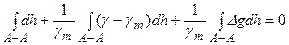 . (5.39)
. (5.39)
Теоретична нев’язка 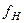 в такому полігоні визначиться, як
в такому полігоні визначиться, як
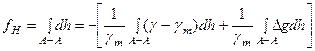 . (5.40)
. (5.40)
Дата добавления: 2015-07-24; просмотров: 1012;