Ортометричні висоти

Різниця потенцілів сили ваги між точками, що знаходяться на різних рівневих поверхнях, буде визначатися формулою (5.2), а її числове значення 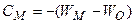у поточній точці М і у нуль-пункті нівелювання О (див. рис.5.2), взята з оберненим знаком називається геопотенціальною величиною. Якщо між точками О і М виконано геометричне нівелювання та виміряні значення сили ваги g в точках стояння рейок, то геопотенціальна величина С_М точки М відносно точки О знайдеться за формулою

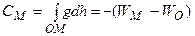, (5.31)

Геопотенціальна величина 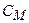не залежить від шляху нівелювання. Безпосередньо прирости геопотенціальних величин можуть використовуватися при врівноваженні полігонів геометричного нівелювання, оскільки теоретична сума цих приростів в замкнутому полігоні дорівнює нулю.

Відрізок 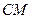(див. рис. 5.2) представляє відстань від нуль-пункта висот – геоїда до фізичної поверхні Землі, яку називають ортометричною висотою точки 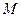і позначають 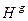. Отже, ортометрична висота – це висота точки фізичної поверхні Землі над поверхнею геоїда, відкладена по силових лініях поля сили ваги (чи по прямовисних лініях), що проходять через цю точку. Числове значення ортометричної висоти H^g одержують діленням геопотенціальної величини С_М на середнє інтегральне (можна брати середнє) значення сили ваги 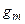вздовж силової лінії (чи відрізка прямовисної лінії) СМ, тобто

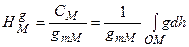. (5.32)

Для точок одної і тої ж рівневої поверхні ортометричні висоти будуть різними настільки, наскільки різними є значення в різних точках одної і тої ж рівневої поверхні. Проте отримати ортометричну висоту точки за формулою (5.32) є проблематичним. Якщо значення інтегралу можна знайти порівняно легко (потрібно виміряти перевищення та знати прискорення сили ваги вздовж нівелірної траси), то величину визначити точно неможливо. Для її визначення, необхідно знати густину мас, що лежать між фізичною поверхнею Землі і геоїдом в кожній точці силової лінії. Величина може бути розрахована при певних модельних припущеннях розподілу сили ваги або густини в земній корі.

В результаті перетвореня формулу (5.32), опускаючи індекси для конкретної точки, приводять до наступного вигляду

. (5.33)

В цьому рівнянні перший інтеграл дає виміряну висоту, другий – поправку у виміряну висоту за непаралельність рівневих поверхонь нормального потенціалу, третій та четвертий дають поправки, що обумовлені аномаліями сили ваги.

При застосуванні ортометричної системи висот геодезична висота точки 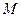(див. рис. 5.2) визначиться як сума її складових

,

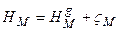де 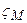-висота геоїда над поверхнею еліпсоїда.