Астрономічне нівелювання

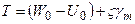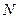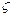Часткові похідні збурюючого потенціалу (тут проведена заміна на ) будуть дорівнювати

.

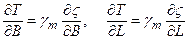Підставимо знайдені значення часткових похідних у формулу (5.14) і отримаємо нові вирази для складових відхилень прямовисних ліній

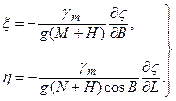(5.24)

Обчислимо диференційну зміну відступів геоїда 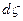, використовуючи топоцентричну горизонтальну систему координат 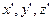(див. § 1.4). Якщо висота геоїда є функцією цих координат, тобто 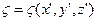, то його повний диференціал буде

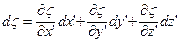. (5.25)

Згідно формули (3.47) має місце ортогональне перетворення координат, тобто відрізки

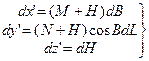(5.26)

складають ортогональну систему координат. З використанням (5.24) та (5.26) для часткових похідних отримаємо

.

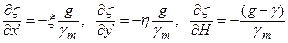Зауважимо, що часткова похідна по висоті приведена нами без доведення (детальніше див. [9]). Тепер формулу (5.25) можна записати у такому вигляді

.

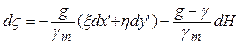Поскільки 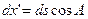та 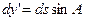(див. формулу 3.1), то

.

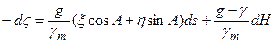Проінтегрувавши останній вираз по ходовій лінії між точками 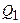та 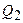на земній поверхні, отримаємо перевищення геоїда між цими точками

. (5.27)

Формула (5.27) і є формулою астрономічного нівелювання. У цій формулі перший інтеграл є головним, а другий – малою поправкою за відносний надлишок сили ваги.

Отже, сам процес астрономічного нівелювання полягає в наступному. Вздовж вибраної траси повинні бути визначені астрономічні та геодезичні координати точок, взятих на відстанях 5-10 км, їх наближені висоти (будь-яким методом). Необхідно також провести гравіметричне знімання. Після отримання всіх необхідних даних визначають 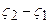. Звісно, в початковій точці астрономічного нівелювання висота геоїда над земним еліпсоїдом повинна бути відома. Отримання різниць 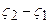за формулою (5.27) є досить складною справою, особливо це стосується обчислення другого члена. Взагалі ця поправка є порівняно незначною: в гірських районах вона може складати до 0.5м, а у рівнинних – до 0.1м. Зважаючи на величину даної поправки, а також на той факт, що вона визначається досить невпевнено, нею часто нехтують. Тому формулу астрономічного нівелювання часто записують у спрощеному варіанті

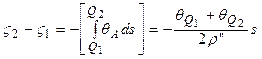, (5.28)

де .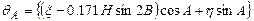

Похибка лінійної інтерполяції астрономо-геодезичних відхилень прямовисних ліній 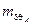визначається для рівнинних районів виразом (5.21). Емпірична середня квадратична похибка астрономічного нівелювання (в м) по лінії довжиною 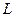підраховується за формулою

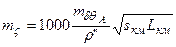, (5.29)

де 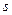-відстань між астропунктами. Для типової в Україні відстані 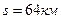маємо 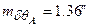. Тоді при .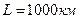

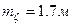Результати астрономічного нівелювання можуть бути суттєво покращені, якщо замість збільшення кількості астропунктів використати інтерпольовані значення астрономо-геодезичних відхилень прямовисних ліній (див. § 5.2.3). Використання інтерпольованих відхилень прямовисних ліній зменшує вплив нелінійності зміни астрономо-геодезичних відхилень прямовисних ліній, але цілком не виключає його.