Гравіметричні відхилення прямовисних ліній
Поскільки відхилення прямовисної лінії є кут між нормалями до рівневих поверхонь дійсного і нормального гравітаційного полів, то, очевидно, має місце функціональний зв’язок між відхиленнями прямовисних ліній та аномаліями сили ваги, тобто 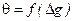 . Термін “гравіметричні” означає, що відхилення прямовисних ліній визначають на основі вимірювань прискорення сили ваги методами гравіметрії.
. Термін “гравіметричні” означає, що відхилення прямовисних ліній визначають на основі вимірювань прискорення сили ваги методами гравіметрії.
Кут між нормаллю до рівневого еліпсоїда та прямовисною лінією на земній поверхні будемо представляти його складовими в площинах меридіана і першого вертикалу [9]
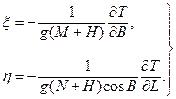 (5.14)
(5.14)
Знак “-“ поставлений через те, що додатні відхилення прямовисних ліній збільшують геодезичну широту і довготу і поправку треба вводити із знаком мінус.
Формула (5.14) відображає залежність між відхиленням прямовисних ліній та збурюючим потенціалом сили ваги 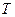 . Згідно [9], збурюючий потенціал
. Згідно [9], збурюючий потенціал 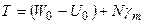 . Тоді, приймаючи
. Тоді, приймаючи 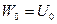 , для часткових похідних запишемо
, для часткових похідних запишемо
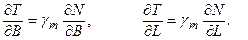
Підставимо знайдені значення часткових похідних у формулу (5.14), вважаючи при цьому, що 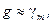 а
а 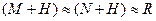 - середньому радіусу кривини еліпсоїда в даній точці. Отримаємо
- середньому радіусу кривини еліпсоїда в даній точці. Отримаємо
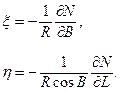 (5.15)
(5.15)
Значення висоти геоїда 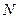 задається формулою Стокса [11]]
задається формулою Стокса [11]]
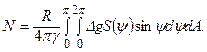
Оскільки 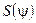 явно від
явно від  і
і 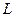 не залежить і, враховуючи, що кінцевість підінтегрального виразу дозволяє диференціювати під знаком інтегралу, то будемо мати
не залежить і, враховуючи, що кінцевість підінтегрального виразу дозволяє диференціювати під знаком інтегралу, то будемо мати
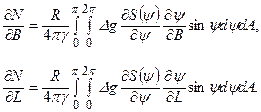 (5.16)
(5.16)
Похідні 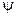 по
по  і
і 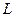 мають наступні значення
мають наступні значення
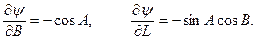 (5.17)
(5.17)
Позначимо
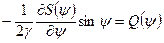 . (5.18)
. (5.18)
Тоді, з врахуванням (5.16-5.18) формули (5.15) отримають наступний вигляд
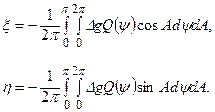 (5.19)
(5.19)
Формули (5.19) називаються формулами Венінг-Мейнеса, а вираз (5.18) – функцією Венінг-Мейнеса. Вказані формули дають значення відхилень прямовисних ліній на поверхні геоїда в меридіані та у напрямі першого вертикалу за відомими аномаліями сили ваги на цій поверхні.
Опустивши викладки з диференціюванням формули Стокса, напишемо для функції Венінг-Мейнеса (5.18) розгорнутий вираз
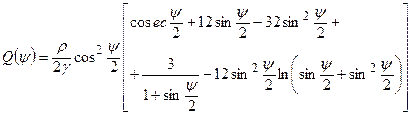 (5.20)
(5.20)
При практичному обчисленні відхилень прямовисних ліній праву частину формул (5.19) поділяють на три частини, що відповідають трьом областям інтегрування: центральній області радіуса 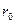 , в якій градієнт сили ваги за вибраними напрями
, в якій градієнт сили ваги за вибраними напрями 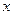 і
і 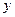 можна вважати сталими (
можна вважати сталими ( 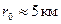 ), а поверхню сфери в її межах – горизонтальною площиною; ближній кільцевій зоні радіуса
), а поверхню сфери в її межах – горизонтальною площиною; ближній кільцевій зоні радіуса 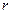 (
( 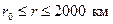 ), в якій можна знехтувати кривиною Землі; далеким зонам, в яких кривина Землі враховується (
), в якій можна знехтувати кривиною Землі; далеким зонам, в яких кривина Землі враховується (  ). Кожна область, за виключенням центральної, розбивається радіальними напрямами на сферичні трапеції. Для кожної трапеції повинно бути відомо середнє значення аномалії сили ваги
). Кожна область, за виключенням центральної, розбивається радіальними напрямами на сферичні трапеції. Для кожної трапеції повинно бути відомо середнє значення аномалії сили ваги 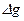 . В курсі фізичної геодезії приводиться детальний виклад методики обчислення відхилень прямовисних ліній з застосуванням чисельних способів розв’язування інтегралів (5.19). Вкажемо лише на те, що обчислення в усіх трьох областях інтегрування представляє собою “абсолютне” відхилення прямовисних ліній. Лапки “ “ означають, що теоретично це можливо, але практично даних про аномалії сили ваги по всій поверхні Землі завжди є недостатньо, тому досить часто інтегрування ведеться тільки у області до
. В курсі фізичної геодезії приводиться детальний виклад методики обчислення відхилень прямовисних ліній з застосуванням чисельних способів розв’язування інтегралів (5.19). Вкажемо лише на те, що обчислення в усіх трьох областях інтегрування представляє собою “абсолютне” відхилення прямовисних ліній. Лапки “ “ означають, що теоретично це можливо, але практично даних про аномалії сили ваги по всій поверхні Землі завжди є недостатньо, тому досить часто інтегрування ведеться тільки у області до 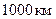 від досліджуваного пункту. На даний час врахування далеких зон можна виконувати за глобальними гравітаційними моделями.
від досліджуваного пункту. На даний час врахування далеких зон можна виконувати за глобальними гравітаційними моделями.
При оцінці точності визначення гравіметричних відхилень прямовисних ліній необхідно взяти до уваги систематичні похибки впливу далеких зон, обумовлені відсутністю даних про аномалії сили ваги або похибками інтерполювання аномалій для тих трапецій, де вони не визначалися. Крім систематичних будуть мати місце випадкові похибки врахування місцевих (локальних) полів аномалій сили ваги. Якщо рівномірне гравіметричне знімання виконане для всієї поверхні Землі, то похибка визначення абсолютних відхилень прямовисних ліній буде залежати тільки від точності визначення гравіметричних характеристик для відповідних ділянок земної поверхні. Її можна підрахувати за формулою
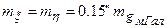 ,
,
де  - похибка гравіметричного визначення прискорення сили ваги, яка залежить точності самих гравіметричних вимірів, від густоти знімання та від похибки інтерполювання до центральної точки трапеції. Для похибки
- похибка гравіметричного визначення прискорення сили ваги, яка залежить точності самих гравіметричних вимірів, від густоти знімання та від похибки інтерполювання до центральної точки трапеції. Для похибки  похибки гравіметричних відхилень прямовисних ліній будуть складати
похибки гравіметричних відхилень прямовисних ліній будуть складати 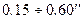 .
.
Дата добавления: 2015-07-24; просмотров: 2058;
