Сучасні поняття про фігуру Землі та її зовнішнє гравітаційне поле

Розміри Землі і форма її поверхні як в цілому, так і окремих частин є предметом вивчення різних дисциплін (фізична геодезія або теорія фігури Землі, фізика Землі, теоретична геофізика тощо), в яких ці питання розглядаються з неоднакових позицій і різними методами, що обумовлено своїми специфічними задачами. Поняття “фігура Землі” є неоднозначним і має різне трактування в залежності від використання отримуваних даних.

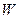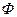З фізичної геодезії відомо, що потенціал сили ваги Землі визначається як сума потенціалу притягання Землі і потенціалу відцентрової сили . Відповідно, потенціал притяганняв теорії фігури Землі це є потенціал сили притягання одиничної маси в довільній точці простору 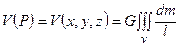всіма масами планети Земля, а потенціал відцентрової сили Землі – це потенціал сили, яка виникає під час обертання Землі навколо своєї осі і діє на одиничну масу на поверхні планети або в найближчому її околі . 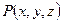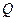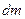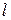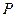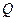У цих виразах: позначає точку, в якій обчислюється, – змінна точка всередині тіла Землі, яка приймає зміст центра мас елемента , - відстань між і (просторова пряма лінія), – Ньютонова гравітаційна стала ( 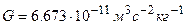), 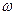- кутова швидкість обертання Землі. Отже,

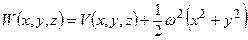. (5.1)

Якщо позначити силу ваги або прискорення сили ваги через 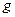і знати потенціал сили ваги 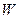даної точки, то можна обчислити складові сили ваги по осях координат

,

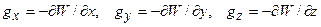а, знаючи складові сили ваги легко можна визначити модуль вектора прискорення сили ваги

,

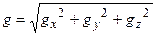та його напрям

.

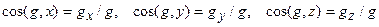Фізична поверхня Землі в межах континентальної частини з її відносними підвищеннями та пониженнями не є правильною математичною поверхнею і не може бути виражена яким-небудь математичним рівнянням. Звідси виникла задача встановлення поняття і вибору математичної поверхні Землі.

Оскільки фізична поверхня Землі складається переважно із поверхні морів та океанів (загальна площа материків складає приблизно лише четверту частину всієї поверхні Землі, а їх середня висота над рівнем Світового океану дорівнює тільки десятитисячній частині земного радіуса), то в свій час за математичну поверхню Землі умовно була прийнята поверхня Світового океану в стані рівноваги води.

Поверхня води Світового океану як рідка маса, що знаходиться тільки під дією сили земного притягання та відцентрової сили обертання Землі, є однією з рівневих поверхонь потенціала сили ваги. Ця поверхня характеризується тією основною властивістю, що на ній потенціал прискорення сили ваги всюди має одне і теж постійне значення, тобто в кожній її точці напрям нормалі до неї збігається з напрямом дії сили ваги або з прямовисною лінією. Якщо рівневу поверхню Світового океану продовжити під материками так, щоб вона всюди перетинала напрям прямовисної лінії під прямим кутом, то тоді отримається деяка замкнута поверхня, яка і буде характеризувати математичну фігуру Землі.

Вказана властивість будь-якої рівневої поверхні може бути виражена математичним рівнянням,

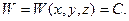(5.1´)

в якому потенціал сили ваги є функцією від координат її поточної точки та розподілу маси всередині тіла, обмеженого заданою рівневою поверхнею. В такій редакції рівнева поверхня, яка збігається з поверхнею Світового океану в стані рівноваги і відповідним чином продовжена під материками, є математичною поверхнею. Проте вигляд або форма цієї поверхні залежать від розподілу сили ваги на ній або внутрішньої будови Землі.

Згодом остаточно вияснилося, що фігура Землі, утворена рівневою поверхнею, яка збігається з поверхнею Світового океану і відповідним чином продовжена під материками, має досить складну форму. Це пояснюється нерівномірним розподілом сили ваги на поверхні Землі і залежить від структури земної кори. Вказана математична поверхня не може бути представлена повністю якою-небудь правильною геометричною фігурою, що має просте математичне рівняння. Для математичної фігури Землі у вказаному її розумінні в 1873 р. був запропонований термін “геоїд”, який закріпився в геодезичній науці до сьогоднішнього часу.

Результати астрономо-геодезичних робіт підтвердили висновки про те, що вказана вище математична поверхня, хоч і відповідає фізичній природі Землі, проте може значно відрізнятися від правильної математичної фігури – загального земного сфероїда – фігури, яка найкращим чином представляє Землю як в гравітаційному так і в геометричному відношенні.

Отже, через те, що дійсне поле сили ваги є математично дуже складним, виділяють (в якості референцного) нормальне поле сили ваги простої аналітичної природи. В загальному, нормальний потенціал сили ваги 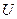вибирається так, що референц-еліпсоїд є еквіпотенціальною поверхнею для :

,

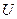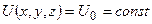а геоїд - еквіпотенціальною поверхнею дійсного потенціала сили ваги :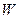

.

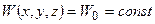Відмінність потенціала сили ваги реальної Землі 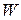від потенціала сили ваги Нормальної Землі 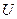носить назву збурюючого потенціала, тобто .

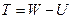Для обчислення нормальної сили ваги 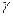на еліпсоїді служить замкнута формула Сомільяна

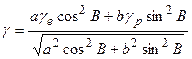, (5.1´´)

де 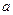і - параметри еліпсоїда, і 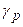позначають нормальну силу ваги на екваторі і полюсі відповідно.

Отже, найбільш відомою узагальненою фігурою Землі є загальний земний сфероїд, точнішне рівневий еліпсоїд обертання, який ще називають Нормальна Земля. Під цим терміном розуміється узагальнена модель Землі як планети в цілому, яка з однієї сторони відтворює її основні властивості в усередненому вигляді, а з другої – найбільш просто представляє її для математичного опису.

Нормальна Земля при розв’язуванні наукових і практичних задач виконує двояку роль: вона застосовується або як правдоподібна модель Землі, яка з достатньою точністю замінює реальну Землю (в астрономії, геофізиці, картографії, навігації тощо), або там, де вимагається більш висока точність, як досить добре її перше наближення ( в геодезії, гравіметрії, космічній геодезії тощо).

Чисто теоретично при вивченні фігури Землі у відношенні її виду та розмірів можна було би розглядати будь-яку із її рівневих поверхонь, оскільки від одної із них можна теоретично перейти до іншої рівневої поверхні. Для переходу від даної або вихідної рівневої поверхні 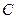до другої нескінченно близької до неї рівневої поверхні 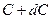, розташованої на висоті 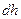, можна було би застосувати наступну формулу

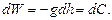(5.2)

Але для переходу від одної рівневої поверхні до другої, як показує формула (5.2), необхідно знати закон зміни сили ваги 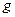з висотою. Оскільки закон зміни сили ваги з висотою всередині земної маси точно не відомий, то теоретична можливість переходу від одної рівневої поверхні до другої рівневої поверхні Землі не може бути здійснена строго у практичному відношенні.

Вибір і вивчення довільної рівневої поверхні для того, щоб потім визначати відносно неї елементи конкретно заданої рівневої поверхні теж не може бути абсолютно умовним. Для геодезії особливе значення має вивчення вигляду і розмірів безпосередньо тієї рівневої поверхні, яка проходить близько до фізичної поверхні Землі та найкращим чином характеризує її дійсну фігуру. Зрозуміло, що вона має бути вибрана у повній відповідності до будови і характеру зовнішньої поверхні Землі як планети в цілому. Це означає, що нормальний потенціал 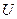необхідно встановити так, щоб збурюючий потенціал 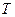був гармонійною функцією з високою точністю наближення.

5.2. Відхилення прямовисних ліній та відступи геоїда від земного еліпсоїда

Напрям сили ваги в деякій точці, або напрям прямовисної лінії повністю визначається виглядом рівневої поверхні в цій точці. Визначає вигляд рівневої поверхні, а, відповідно, і напрям прямовисних ліній розподіл мас в земній поверхні. Це ж саме стосується і відступів геоїда від земного еліпсоїда: відступи обумовлені існуючим розподілом мас на земній поверхні і всередині її та відповідають цьому розподілу.

Порушення певного розподілу мас, при якому густина речовини змінюється в горизонтальному напрямі (має різні значення в різних місцях на одній глибині), охоплюють лише зовнішній шар Землі, товщина якого не перевищує 70 км. В порівнянні з розмірами та масою всієї Землі така незначна величина означає, що відступи геоїда від еліпсоїда та відхилення прямовисних ліній від нормалей до цього еліпсоїда повинні бути малими величинами.

На основі сучасної моделі гравітаційного поля EGM96 можна характеризувати відступи геоїда від загального земного еліпсоїда. Доказаним фактом є існування глобальних хвиль геоїда, тобто загальних відступів його від земного еліпсоїда. Висоти цих хвиль складають до 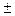70 м, а їхня зміна має як довготний так і широтний характер. Цим глобальним відступам геоїда відповідають і глобальні відхилення прямовисних ліній від нормалей до еліпсоїда (до 10 .

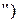Місцеві особливості будови земної кори викликають локальні хвилі геоїда, яким відповідають і локальні відхилення прямовисної лінії. Причинами, що викликають локальний характер, можуть бути аномальне залягання порід всередині земної кори, берегові лінії океанів та морів, гірські утворення тощо. Місцеві відступи геоїда представлені, переважно, у вигляді порівняно незначних хвиль, що мають невелику висоту та область поширення. Проте відповідні їм локальні відхилення прямовисної лінії можуть досягати дуже значних величин (десятків секунд дуги), що є наслідком значної зміни кривини рівневої поверхні.

Коли йде мова про відступи геоїда від земного еліпсоїда та відповідні відхилення прямовисних ліній, то ми повинні чітко зрозуміти про які параметри йдеться.

Відступи геоїда над земним еліпсоїдом – це перевищення точок геоїда відносно поверхні еліпсоїда. Вони не можуть бути виміряні безпосередньо. Результати астрономо-геодезичних і гравіметричних вимірювань, віднесені до поверхні певного еліпсоїда, дають тільки похідні величини або градієнти відступів геоїда від поверхні віднесення. Дослідження фігури геоїда і полягає у визначені її відступів від фігури еліпсоїда за похідними від них величинами, якими і є відхилення прямовисних ліній та аномалії сили ваги 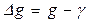, що безпосередньо обчислюються за даними вимірювань.

Якщо відхилення прямовисної лінії визначають як кут між нормаллю до поверхні загального земного еліпсоїда і напрямом прямовисної лінії, то називають його абсолютним відхиленням прямовисної лінії. Якщо ж до уваги береться нормаль до поверхні референц-еліпсоїда - то отримують відносне відхилення прямовисної лінії.

Абсолютні відхилення прямовисної лінії залежать тільки від розподілу мас Землі. Відносні відхилення прямовисної лінії залежать від розподілу мас Землі, прийнятих параметрів і орієнтування референц-еліпсоїда. Очевидно, що відносні відхилення прямовисної лінії можуть значно відрізнятися від абсолютних в тих же точках і через них ми не можемо безпосередньо робити висновки про характер неправильностей у будові земної кори.

Напрям прямовисної лінії визначається на земній поверхні з астрономічних спостережень через визначення астрономічних координат - широти та довготи 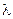. Напрям нормалі до поверхні референц-еліпсоїда визначається геодезичними координатами і 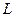. Звідси випливає, що відхилення прямовисних ліній можна визначити через співставлення астрономічних і геодезичних координат. Оскільки геодезичні координати традиційно визначаються на поверхні референц-еліпсоїда за результатами лінійних і кутових вимірювань на фізичній поверхні Землі, то відхилення прямовисної лінії називають також відносними астрономо-геодезичними. Відзначимо, що при обчислені геодезичних координат на основі результатів супутникових спостережень, із порівняння їх з відповідними астрономічними координатами отримаємо абсолютні астрономо-“геодезичні” відхилення прямовисних ліній.

Напрям прямовисної лінії в даній точці земної поверхні збігається з напрямом нормалі до рівневої поверхні потенціалу сили ваги 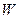в цій же точці або, точніше, з дотичною до силової лінії дійсного поля сили ваги. Напрям нормалі до земного еліпсоїда збігається з дотичною до силової лінії нормального поля сили ваги. Звідси, відхилення прямовисної лінії можна визначити як кут між дотичними до силових ліній дійсного і нормального полів сили ваги. В такому сенсі його називають гравіметричним відхиленням прямовисної лінії або відхиленням важка.

Одна із причин появи відхилень прямовисних ліній – притягання надлишкових мас на материках і недостатність цих притягальних мас в океанах. І хоча зміна зовнішніх (топографічних) форм рельєфу не є домінуючою як зміна густини порід земної кори, все ж форми топографічного рельєфу вносять певний вплив на знак і величину відхилень прямовисних ліній. Цей вплив дещо послаблюється через так звану ізостатичну компенсацію або ізостазію. Відхилення прямовисних ліній, що визначаються на основі впливу топографічних мас з врахуванням явища ізостазії, називаються топографо-ізостатичними відхиленнями.

Відступи геоїда від земного еліпсоїда теж можна класифікувати на абсолютні – висоти геоїда над загальним земним еліпсоїдом (позначається через 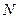) та відносні – висоти геоїда над референц-еліпсоїдом (позначається через ).

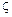Відмітимо значення відступів геоїда та відхилень прямовисних ліній.

Відступи (висоти) геоїда над референц-еліпсоїдом, як і відхилення прямовисних ліній, безпосередньо використовуються при вивченні фігури Землі: виводі параметрів земного еліпсоїда; встановленні вихідних геодезичних дат; визначенні взаємного орієнтування різних геодезичних систем координат.

З використанням висот геоїда та відхилень прямовисних ліній розв’язують багато редукційних задач вищої геодезії.

Через відхилення прямовисних ліній встановлюється прямий зв’язок між астрономічними і геодезичним координатами.

За допомогою відхилень прямовисних ліній здійснюється перехід від безпосередньо виміряного астрономічного азимута до геодезичного азимута.

Відхилення прямовисних ліній необхідні при класичному методі визначення геодезичних висот.