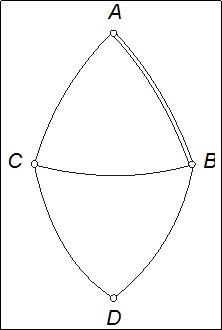
Числовий приклад опрацювання фрагменту геодезичної мережі на площині в проекції Гаусса-Крюгера.
Нехай фрагмент геодезичної мережі (тріангуляції) 2-го класу складається з двох трикутників (рис.4.8), сторона одного з них  є вихідною стороною даної мережі, тобто відомо її довжина і геодезичний азимут; відомо також геодезичні координати вихідного пункта
є вихідною стороною даної мережі, тобто відомо її довжина і геодезичний азимут; відомо також геодезичні координати вихідного пункта 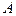 :
:
|
L1 =21о 50’11.3692”
A12=177о 15’41.494”
S12 =24796.232 м
|
Таблиця 4.7
| Назва вершин | Виміряні та приведені до еліпсоїда кути |
| С B A | 55о54’45.56” 55 46 30.66 68 18 46.67 |
| D C B | 60o 52’14.52” 56 19 23.45 62 48 23.90 |
Всі обчислення виконують для триградусної зони в послідовності, яка вказана у параграфі 4.6, наступним чином:
1) Обчислення плоских прямокутних координат пункта  за його геодезичними координатами; виконується за формулами (4.19). Перед обчисленнями координат проводять встановлення номера триградусної зони, в якій розташований пункт
за його геодезичними координатами; виконується за формулами (4.19). Перед обчисленнями координат проводять встановлення номера триградусної зони, в якій розташований пункт  та довготи осьового меридіана
та довготи осьового меридіана 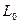 :
:
 ,
,
а потім обчислюють самі координати та зближення меридіанів:
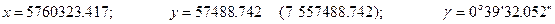 ;
;
для контролю проводять обчислення геодезичних координат вихідного пункту за отриманими плоскими прямокутними на основі формул (4.20). При цьому значення величини 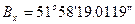 , а
, а 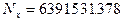 .
.
2) Попереднє (наближене) розв’язування трикутників проводиться з метою обчислення наближених довжин сторін мережі, які необхідні в свою чергу для обчислення сферичних надлишків трикутників та наближених координат пунктів. Сторони обчислюються за формулами плоскої тригонометрії (теоремою синусів), а сферичний надлишок за формулою (3.4). Результати обчислень приведені в таблиці 4.8.
Таблиця 4.8
| № трикутника | Трикутники | Довжини сторін, м | Сферичний надлишок |
1   
| B c a A C b | c=24796 b=24756 a=27821 |
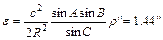
|
   2 2
| B d c C D b | d=27821 b=28329 c=26504 |
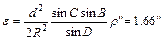
|
3) Дирекційний кут 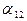 хорди зображення геодезичної лінії початкової сторони на площині обчислюється за формулою (4.11). Поскільки значення поправки
хорди зображення геодезичної лінії початкової сторони на площині обчислюється за формулою (4.11). Поскільки значення поправки 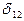 поки що нам невідоме, то можемо знайти тільки наближене значення дирекійного кута:
поки що нам невідоме, то можемо знайти тільки наближене значення дирекійного кута:
 .
.
4) Обчислення наближених координат пунктів, необхідних для визначення поправок 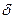 , а також приведення довжини вихідної сторони на площину в проекції наведено у таблиці 4.9.
, а також приведення довжини вихідної сторони на площину в проекції наведено у таблиці 4.9.
Таблиця 4.9
| Елементи | A(1) | A(1) | B(1) | B(1) | C(1) | |
| B(2) | C(2) | D(2) | ||||
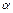 кут
кут
| 176036’09” | 176036’09” 68018’47” | 356036’09” 55046’31” | 300049’38” 62048’24” | 120049’38” 56019’23” | |
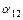
| 176036’09” | 244054’56” | 300049’38” | 238001’16” | 177009’01” | |
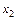
| ||||||
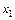
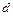
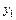
| ||||||
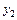
| ||||||
5) Обчислення поправок 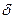 за формулою (4.31) проводять згідно таблиці 4.10.
за формулою (4.31) проводять згідно таблиці 4.10.
Таблиця 4.10
| Елементи | A(1) | A(1) | B(1) | B(1) | C(1) |
| B(2) | C(2) | D(2) | |||
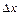
| -24752 | -10495 | -14037 | -28294 | |
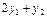
| |||||
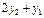
| |||||
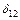
| -3.632 | -1.329 | 1.840 | -1.828 | -2.545 |

| 3.663 | 1.130 | -1.553 | 1.562 | 2.579 |
6) Введення поправок у виміряні напрями та врівноваження кутів за умови сум виконують згідно таблиці 4.11.
Таблиця 4.11
| № трикутника | Назва кута | Виміряні та приведені до поверхні еліпсоїда кути | Поправки в кути
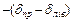
| Поправки за врівноваження | Врівноважені плоскі кути |
| C B A | 55о54’45.56” 55 46 30.66 68 18 46.67 | -2.683 1.823 2.304 | -0.482 -0.482 -0.482 | 55о54’47.76” 55 46 28.36 68 18 43.88 | |
| 180 00 02.89 | 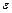 =1.444 =1.444
| 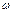 =1.446 =1.446
| 180 00 00.00 | ||
| D C B | 60o 52’14.52” 56 19 23.45 62 48 23.90 | -1.016 -0.992 3.669 | -0.07 -0.07 -0.07 | 60o 52’15.47” 56 19 24.37 62 48 20.16 | |
| 180 00 01.87 | 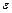 =1.660 =1.660
| 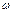 =0.210 =0.210
| 180 00 00.00 |
7) Обчислення довжини вихідної сторони на площині (довжини хорди зображення геодезичної лінії) за формулою (4.36)
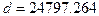 м.
м.
8) Обчислення остаточного значення дирекційного кута вихідної сторони на площині за формулою (4.11)
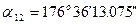 .
.
Дата добавления: 2015-07-24; просмотров: 714;