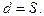Формули для редукування напрямів і відстаней
Під редукуванням напрямів і відстаней розуміють перехід від напрямів і довжин геодезичних ліній на еліпсоїді до відповідних їм величин на площині. Редукція напрямів полягає у визначенні поправки за кривину зображення геодезичної лінії на площині, а редукція відстаней - знаходженні різниці довжини геодезичної лінії та хорди зображення геодезичної лінії. Після введення цих редукцій у виміряні величини, які приведені на поверхню еліпсоїда, ми отримаємо геодезичну мережу, редуковану з еліпсоїда на площину.
На практиці редукування мережі 1–го класу на площину проводиться тільки в окремих випадках і не має широкого розповсюдження, тому при виводі формул будемо орієнтуватися на мережі нижчих (2-4) класів.
Для редукування напрямів вважатимемо, що AB є геодезичною лінією на поверхні еліпсоїда в складі деякої замкнутої геодезичної фігури ABDC (рис. 4.5.б).
|
а) б)
Рис.4.5
Нехай геодезична лінія AB зображена на площині в виді кривої 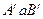 (рис. 4.5.а). Кути в точках
(рис. 4.5.а). Кути в точках 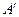 і
і  між дотичними до кривої і хордою
між дотичними до кривої і хордою  позначимо через
позначимо через 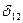 і
і  . Координати точок
. Координати точок 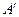 і
і  позначимо через
позначимо через  і
і 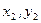 . Нехай точки
. Нехай точки 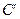 і
і 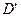 є основами ординат точок
є основами ординат точок 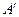 і
і  відповідно. Із-за конформності проекції фігури ABCD і A’B’C’D’ будуть подібними, а відповідні кути у них рівними. Суми внутрішніх кутів складуть:
відповідно. Із-за конформності проекції фігури ABCD і A’B’C’D’ будуть подібними, а відповідні кути у них рівними. Суми внутрішніх кутів складуть:
· на еліпсоїді  ;
;
· на площині 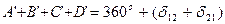 .
.
Значить, 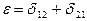 , тобто сферичний надлишок рівний сумі поправок взаємнообернених напрямів. Як відомо (див. розділ 3), сферичний надлишок визначається формулою
, тобто сферичний надлишок рівний сумі поправок взаємнообернених напрямів. Як відомо (див. розділ 3), сферичний надлишок визначається формулою
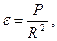
де 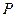 - площа фігури A’B’C’D’;
- площа фігури A’B’C’D’; 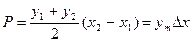 .
.
Тоді
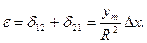
Приймаючи наближено,  , отримуємо
, отримуємо
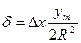 . (4.30)
. (4.30)
На практиці потрібно знати не тільки величину кута  для даного напряму, але і як ввести його в цей напрям, щоб перейти на площині від кривих ліній до їхніх хорд. Оскільки відрахування кутів ведеться за ходом годинникової стрілки, то із рис. 4.5.а) легко видно, що для переходу від напряму
для даного напряму, але і як ввести його в цей напрям, щоб перейти на площині від кривих ліній до їхніх хорд. Оскільки відрахування кутів ведеться за ходом годинникової стрілки, то із рис. 4.5.а) легко видно, що для переходу від напряму  до хорди
до хорди  кут
кут  при точці
при точці  потрібно відняти від напряму
потрібно відняти від напряму  , а при точці
, а при точці 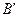 - додати до напряму
- додати до напряму  . Отже, поправки
. Отже, поправки 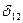 і
і  у взаємні напрями мають протилежні знаки:
у взаємні напрями мають протилежні знаки:
 (4.31)
(4.31)
Формулами (4.31) користуються для редукування напрямів в тріангуляції 3 класу і нижче.
Поправки за редукцію 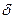 алгебраїчно віднімаються від виміряних напрямів.
алгебраїчно віднімаються від виміряних напрямів.
Значення редукованих плоских кутів A’,B’ і C’ за виміряними на фізичній поверхні і приведеними на еліпсоїд кутами A,B і C трикутника ABC отримують наступним чином
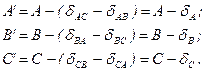
Сума поправок за редукцію кутів трикутника рівна його сферичному надлишку з оберненим знаком, що служить контролем обчислення  та
та 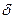 . Справді,
. Справді,
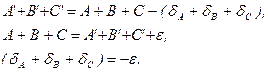
В тріангуляції 2-го класу для обчислення поправок за кривину зображення геодезичних ліній застосовують більш точні формули, які приведемо без доведення
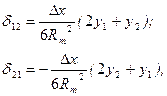 (4.32)
(4.32)
де  - середній радіус кривини, обчислений за широтою середньої точки заданої геодезичної лінії.
- середній радіус кривини, обчислений за широтою середньої точки заданої геодезичної лінії.
Як видно з наведених формул, для обчислення редукцій повинні бути відомі плоскі прямокутні координати початкового і кінцевого пунктів. Визначимо необхідну точність цих координат. Для цього достатньо дослідити формулу (4.30). Продиференціювавши дану формулу за координатами 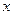 і
і 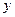 , знаходимо
, знаходимо
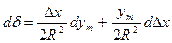 .
.
Позначивши 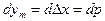 , отримаємо
, отримаємо
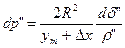 .
.
Нехай:
· для тріангуляції 2-го класу 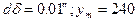 км (на краю шестиградусної зони);
км (на краю шестиградусної зони);  км, тоді
км, тоді 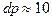 м;
м;
· для тріангуляції 3-го класу 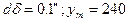 км;
км; 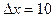 км, тоді
км, тоді  м.
м.
Стосовно опрацювання кутомірних вимірювань нижчих класів (розрядів), то поправки за кривину (в межах шестиградусних зон) можна обчислювати за наближеною формулою:
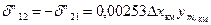 ,
,
а наближені координати пунктів можна вибрати із карти або схеми геодезичної мережі.
Нижче наводиться таблиця абсолютних величин поправок (редукцій) за кривину зображення геодезичної лінії для різних значень 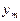 та
та 
Таблиця 4.1
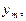  км км
 ,км ,км
| |||||
| 0.6” | 1.2” | 1.9” | 2.5” | 3.2” | |
| 1.3” | 2.5” | 3.8” | 5.1” | 6.4” | |
| 2.5” | 5.0” | 7.7” | 10.1” | 12.6” |
Як видно із таблиці 4.1, в знімальних мережах ( 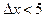 км) поправками за кривину, через їх незначні величини, в порівнянні з похибками вимірювання кутів, можна нехтувати.
км) поправками за кривину, через їх незначні величини, в порівнянні з похибками вимірювання кутів, можна нехтувати.
Перед виводом формул для редукцій відстаней розглянемо спочатку питання про різницю в довжинах зображення дуги геодезичної лінії на площині 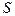 та хорди
та хорди  , шо стягує цю дугу.
, шо стягує цю дугу.
|
|
Рис.4.6
Із (4.12) можемо записати інтеграл
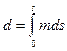 , (4.33)
, (4.33)
де масштаб 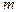 визначається формулою (4.29).
визначається формулою (4.29).
Знайти інтеграл (4.33) в замкнутій формі надзвичайно трудно, поскільки масштаб зображення є досить складною функцією довжини геодезичної лінії. Проте такі фактори як порівняно невелика довжина геодезичної лінії (<30 км) і незначне віддалення від осьового меридіану (  ) спрощують задачу знаходження інтегралу (4.33), і її розв’язання можна буде шукати наближеними методами.
) спрощують задачу знаходження інтегралу (4.33), і її розв’язання можна буде шукати наближеними методами.
Одним із наближених методів обчислення вказаних означених інтегралів є чисельний метод. Конкретно для даного випадку можна застосувати формулу Сімпсона, розділивши інтервал інтегрування на дві частини. Тоді інтеграл (4.33) може бути представлений наступним наближенням
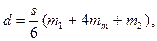 (4.34)
(4.34)
де
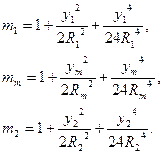 (4.35)
(4.35)
Якщо обчислення проводяться з геодезичними координатами, то для масштабів зображення можна використати формулу (4.27)
При довжинах ліній, що не перевищують 30 км, у всіх трьох виразах для масштабу зображення радіус кривини  можна обчислювати тільки для середньої точки, а в членах четвертого порядку прийняти
можна обчислювати тільки для середньої точки, а в членах четвертого порядку прийняти 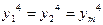 .
.
Для ординат можемо записати такі очевидні співвідношення
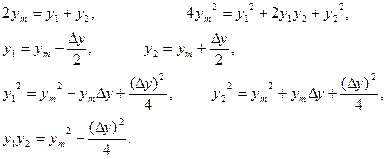
Підставивши в рівняння (4.34) вирази для масштабів (4.35) та використавши приведені вище співвідношення, отримаємо остаточну формулу
 (4.36)
(4.36)
Із отриманої формули видно, що лінія на площині в проекції Гаусса-Крюгера завжди довша від ліній, що зображуються з еліпсоїда. Третій і четвертий члени формули (4.36) при 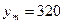 км (максимально можливі значення на краю шестиградусної зони) і
км (максимально можливі значення на краю шестиградусної зони) і 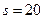 км складають 6 і 8 мм відповідно, тому в роботах, де не вимагається висока точність або коли розміри зони є меншими (
км складають 6 і 8 мм відповідно, тому в роботах, де не вимагається висока точність або коли розміри зони є меншими ( 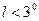 ), можна користуватися формулою
), можна користуватися формулою
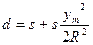 . (4.36’)
. (4.36’)
Підрахуємо тепер, з якою похибкою допустимо знати в (4.36) ординату  середньої точки редукованої лінії.
середньої точки редукованої лінії.
При похибці в  , рівній
, рівній 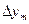 , отримаємо в
, отримаємо в 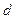 похибку
похибку  , згідно (4.36’), рівну
, згідно (4.36’), рівну
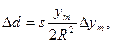
звідки
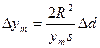 .
.
Якщо поставити вимогу, щоб  не перевищувало 0.001 м, то, приймаючи
не перевищувало 0.001 м, то, приймаючи 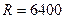 км,
км, 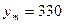 км і
км і 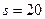 км, отримаємо, що
км, отримаємо, що 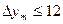 м.
м.
Дата добавления: 2015-07-24; просмотров: 894;


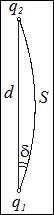
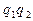 - зображення дуги геодезичної лінії на площині;
- зображення дуги геодезичної лінії на площині; 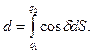 Згідно таблиці 4.1, значення кута
Згідно таблиці 4.1, значення кута 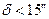 при стандартних довжинах сторін геодезичних мереж. Тому для малих кутів можемо записати
при стандартних довжинах сторін геодезичних мереж. Тому для малих кутів можемо записати
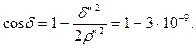 Отже, з похибкою на величину
Отже, з похибкою на величину 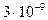 можна прийняти, що
можна прийняти, що 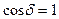 , тоді
, тоді