Формули для обчислення масштабу проекції
Для знаходження формули масштабу зображення скористаємось формулою (4.5), яку представимо у вигляді
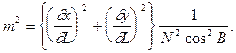 (4.26)
(4.26)
Вирази для часткових похідних нами вже отримано - ф-ли (4.22’). Підставивши квадрати цих виразів у (4.26) і додавши їх, отримаємо
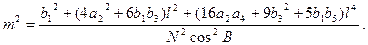
В цій формулі збережено члени порядку 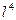 . З врахуванням виразів для
. З врахуванням виразів для 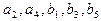 (без сфероїдних членів при
(без сфероїдних членів при 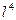 ) та простих алгебраїчних перетворень остаточно знаходимо
) та простих алгебраїчних перетворень остаточно знаходимо
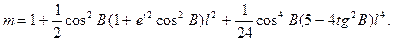 (4.27)
(4.27)
Як видно із даної формули, при 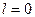 , тобто на осьовому меридіані, масштаб проекції рівний одиниці. При віддалені від осьового меридіана на схід і на захід значення масштабу швидко зростає.
, тобто на осьовому меридіані, масштаб проекції рівний одиниці. При віддалені від осьового меридіана на схід і на захід значення масштабу швидко зростає.
Для отримання формули масштабу зображення у функції плоских прямокутних координат скористаємось другою формулою (4.19), яку, з прийнятими вище обмеженнями, запишемо
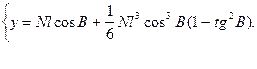
Застосовуючи формули обертання ряду для 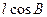 , знайдемо
, знайдемо
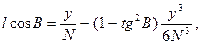
звідки з прийнятою точністю

З врахуванням останніх двох виразів формулу (4.27) можна записати у наступному вигляді
 (4.28)
(4.28)
Оскільки
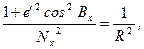
де  - середній радіус кривини еліпсоїда, то остаточно отримаємо
- середній радіус кривини еліпсоїда, то остаточно отримаємо
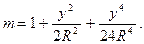 (4.29)
(4.29)
В останньому члені формули (4.29) замість 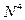 приведено
приведено 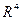 , що викличе похибку порядку
, що викличе похибку порядку 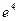 на сфероїдні члени, якими знехтувано у членах порядку
на сфероїдні члени, якими знехтувано у членах порядку 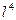 .
.
Масштаб зображення є дуже важливою характеристикою конформної проекції. Згідно формули (4.28) або (4.29) можна встановити величини і розподіл лінійних спотворень при переході з еліпсоїда на площину. Так легко замітити, що із збільшенням ординати 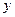 лінійні спотворення зростають пропорційно
лінійні спотворення зростають пропорційно 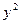 ; постійному значенню ординати
; постійному значенню ординати 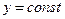 відповідає практично постійна величина масштабу
відповідає практично постійна величина масштабу 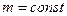 . Величина радіуса
. Величина радіуса
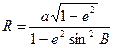
із зміною широти змінюється звісно, але досить незначно. Тому лінії рівних спотворень довжин в проекції Гаусса-Крюгера розташовуються практично паралельно осі абсцис на всій смузі проекції від екватора до полюса, а звідси виходить, що проекцію Гаусса-Крюгера найбільш оптимально застосовувати для зображення смуги, яка витягнута на еліпсоїді з півдня на північ. Межами такої смуги служать лінії рівних спотворень довжин 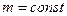 .
.
Дата добавления: 2015-07-24; просмотров: 787;
