Основні рівняння конформної проекції Гаусса.
Як вже було зазначено, в теорії геодезичних проекцій основним є встановлення взаємнооднозначної точкової відповідності між поверхнями земного еліпсоїда і площини таким чином, щоб відповідні кути геометричних фігур еліпсоїда і площини були рівними, а сторони пропорційними. Вказана відповідність визначається законом перетворення заданих геодезичних координат B,L в координати x,y на площині, чи навпаки. Загальні рівняння точкової відповідності можуть бути виражені функціональними залежностями (4.1).
При конформному зображені функції (4.1) повинні задовільняти умовам конформності. Розглянемо коротко ці умови.
Нехай точка А’ є зображенням на площині деякої точки на еліпсоїді А (рис.4.2). Дуги A’B’ і A’C’ - зображення диференціала дуги меридіана та дуги паралелі відповідно.
Кут 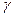 є кутом повороту конформного зображення як меридіана, так і паралелі відносно прямолінійних координатних ліній на площині. Цей кут носить назву з б л и ж е н н я м е р и д і а н і в на площині.
є кутом повороту конформного зображення як меридіана, так і паралелі відносно прямолінійних координатних ліній на площині. Цей кут носить назву з б л и ж е н н я м е р и д і а н і в на площині.
Із подібних трикутників A’B’B” і A’C’C” можемо записати
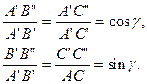 (І)
(І)
Згідно формули (4.2) для масштабу m отримаємо
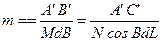 ,
,
звідки
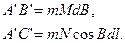 (ІІ)
(ІІ)
|
Рис.4.2
Для зображення диференціалів дуг меридіана і паралелі напишемо повні диференціали плоских прямокутних координат на основі рівнянь (4.1)
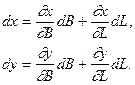
Застосувавши ці рівняння для зображення диференціала дуги меридіана 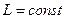 , отримаємо
, отримаємо
 (ІІІ)
(ІІІ)
Аналогічно для зображення диференціала дуги паралелі 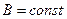 , отримаємо
, отримаємо
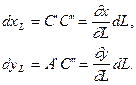 (ІV)
(ІV)
Підставимо значення сторін, що визначаються виразами (ІІ), (ІІІ) і (IV) в рівняння (І). Отримаємо
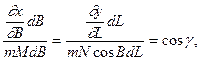
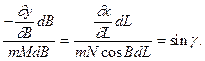
Із наведених співвідношень отримаємо диференційні рівняння
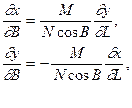 (4.3)
(4.3)
а також формули для визначення 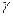 і
і 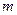
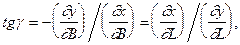 (4.4)
(4.4)
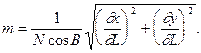 (4.5)
(4.5)
Диференційні рівняння (4.3) є тими умовами, які повинні задовільняти функції (4.1) при конформному зображенні еліпсоїда на площині.
Як вже було зазначено, точкова відповідність між поверхнею еліпсоїда і площиною повинна бути взаємною, тобто повинні існувати і зворотні функції
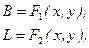 (4.6)
(4.6)
що дозволять перейти від плоских прямокутних координат  до геодезичних
до геодезичних  .
.
Умови, яким повинні задовільняти ці функції при конформному зображенні, визначаються наступними диференційними рівняннями
 (4.7)
(4.7)
Відповідно, зближення меридіанів 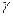 і масштаб зображення
і масштаб зображення 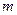 будуть визначатися наступними формулами
будуть визначатися наступними формулами
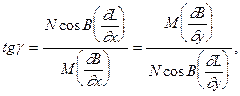 (4.8)
(4.8)
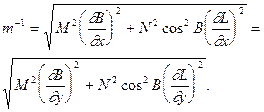 (4.9)
(4.9)
Рівняння (4.3) і (4.7) - основні рівняння конформного перетворення координат. Інтегрування їх виконується при початкових умовах, які задаються при зображенні еліпсоїда на площині чи навпаки.
В проекції Гаусса осьовий меридіан зображується прямою лінією, що приймається за вісь 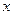 з масштабом m=1, тобто для точок осьового меридіана абсциси рівні дугам меридіана від екватора, а ординати - нулю. Якщо позначити дуги меридіана від екватора до точки заданої широти через X, то для точок осьового меридіана при l=0 отримаємо
з масштабом m=1, тобто для точок осьового меридіана абсциси рівні дугам меридіана від екватора, а ординати - нулю. Якщо позначити дуги меридіана від екватора до точки заданої широти через X, то для точок осьового меридіана при l=0 отримаємо
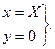 (4.10)
(4.10)
Крім того, додатнім значенням l повинні відповідати додатні значення y і від’ємним l - від’ємні y; додатнім і від’ємним l відповідають тільки додатні значення x (для північної півкулі Землі). Ці умови і визначають проекцію Гаусса.
Дата добавления: 2015-07-24; просмотров: 1115;

