Формули для обчислення координат

а) плоских прямокутних 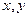за геодезичними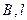

При малій величині різниці довгот 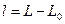залежність між плоскими прямокутними координатами і геодезичними координатами для симетричних проекцій, якою є проекція Гаусса-Крюгера можна представити у вигляді наступних степеневих рядів:

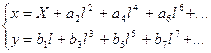(4.15)

де

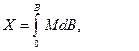
а коефіцієнти в цих рядах є функціями тільки геодезичної широти .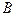

Характерною особливістю рівнянь (4.15) є залежність абсциси від членів парної степені різниці довгот, а ординати - тільки від непарної степені цієї різниці. Такі рівняння ще називають рівняннями симетричних проекцій. Для таких проекцій дві точки еліпсоїда, що мають одинакову широту і одинакову за абсолютною величиною різницю довгот 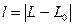, після їх зображення на площині будуть мати одинакову абсцису та одинакову за абсолютною величиною ординату.

Знайдемо значення коефіцієнтів рівнянь (4.15).

Поскільки проекція має бути конформною, то поставимо вимогу, щоб рівняння зображення (4.15) задовільняли умови конформного зображення (4.3).

Підставимо в рівняння (4.3) часткові похідні рядів (4.15) . Тоді отримаємо

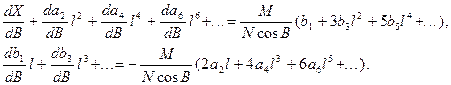
Із порівняння між собою в цих рівностях коефіцієнтів при одинакових степенях 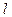, знайдемо

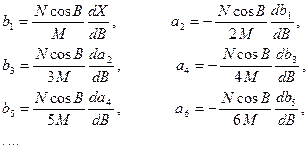
З цих формул видно, що для отримання кожного наступного коефіцієнта необхідно знайти похідну попереднього коефіцієнта. Враховуючи, що

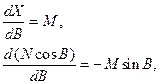
можна легко знайти всі коефіцієнти рядів (4.15).

Приведемо коефіцієнти рядів (4.15) в остаточному вигляді

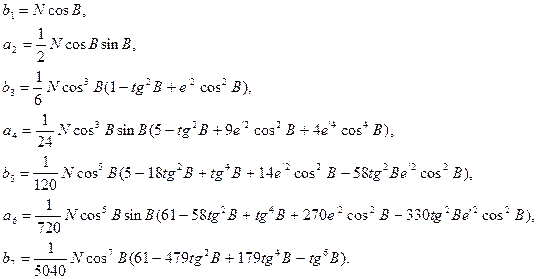(4.16)

Довжину дуги меридіана X від екватора до даної точки з широтою B можна обчислити за формулою (2.50)

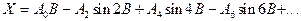(4.17)

де коефіцієнти A₀,A₂,A₄,A₆, що визначаються через параметри прийнятого еліпсоїда (див. ф-лу (2.50¢), для еліпсоїда Красовського мають наступні значення:

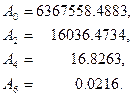(4.18)

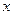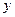Формули (4.15) разом з (4.16)-(4.18) мають високу точність (до 0.001 м в і ) та можуть застосовуватись для різниці довгот 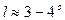, тобто для системи шестиградусних зон. Щодо триградусних зон, то ці формули можна спростити, а саме: в формулі для x можна не враховувати члени з 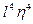та 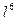, а для y - члени з 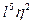та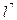

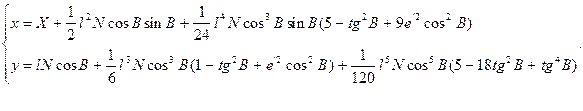(4.19)

Якщо виникає необхідність обчислення координат 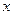і 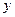з меншою точністю, наприклад, до 1 м, то формули (4.19) з врахуванням коефіцієнтів для еліпсоїда Красовського можна спростити, а саме

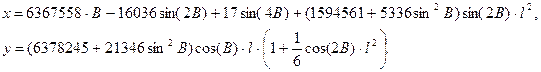(4.19’)

Відмітимо, що у наведених формулах координати 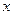і 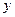отримуємо в метрах, а аргументи 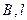при цьому потрібно виразити в радіанах.

б) геодезичних 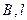за плоскими прямокутними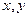

Щоб отримати формули для обчислення геодезичних координат за плоскими прямокутними координатами, представимо функції (4.6) у вигляді рядів за степенями ординати 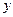, вважаючи її малою величиною. Для симетричних проекцій зображень ці ряди будуть мати вигляд

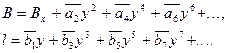(4.20)

Всі коефіцієнти в цих рядах є функціями тільки абсциси .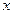

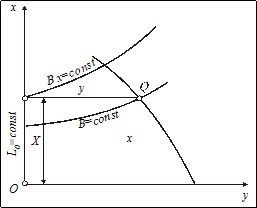
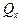Як видно із формул (4.20) і рис.4.4, при величина є широтою точки (рис.4.4).

Рис.4.4

Плоскими прямокутними координатами точки 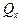є 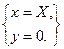, а геодезичними - .

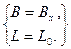Поскільки абсциса цієї точки рівна довжині дуги меридіана , то широту 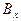можна знайти як функцію довжини дуги меридіана на основі формули (2.56)

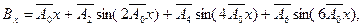
де коефіцієнти 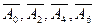для еліпсоїда Красовського будуть мати наступні значення

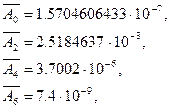
а коефіцієнти рядів (4.20) будуть тоді функціями широти .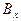

Перейдемо до визначення коефіцієнтів в рядах (4.20). Підставимо в рівняння (4.7) часткові похідні рядів (4.20), де замість аргумента 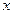будем брати аргумент . Тоді отримаємо

Із порівняння між собою в цих рівностях коефіцієнтів при одинакових степенях 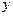, знайдемо

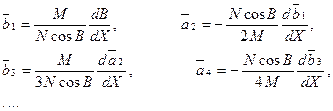
Для знаходження всіх необхідних коефіцієнтів застосовуємо послідовне диференціювання по довжині дуги меридіана , враховуючи при цьому, що

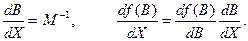
Остаточні значення коефіцієнтів рядів (4.20) мають наступний вигляд

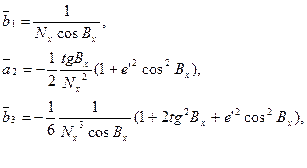(4.21)

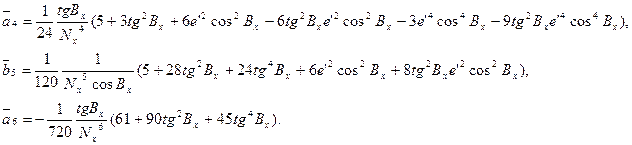
Обчислені таким чином геодезичні координати будуть виражені в радіанній мірі. Точність цих формул така, що вони забезпечують 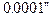в координатах 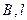при розміщені точки на краю шестиградусної зони.

4.5.2. Формули для обчислення зближення меридіанів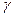

Для визначення зближення меридіанів 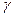скористаємось другою формулою (4.4)

(4.22)

часткові похідні в якій знайдемо на основі формул (4.15). Отримаємо

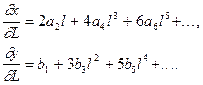(4.22’)

Підставивши значення похідних у (4.22), отримаємо

(4.23)

Значення коефіцієнтів 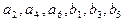даються виразами (4.16), підставивши які в (4.23) і виконавши елементарні математичні перетворення, остаточно отримаємо

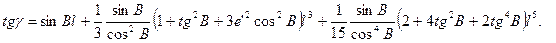(4.24)

Аналогічним чином можна знайти вираз для обчислення зближення меридіанів за плоскими прямокутними координатами, тільки при цьому за вихідну беруть другу формулу (4.8)

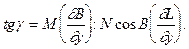
Приведемо остаточну формулу для зближення меридіанів у функції плоских прямокутних координат

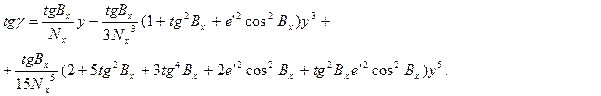(4.25)

У формулах (4.24) і (4.25) не враховано члени з 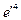. Точність приведених формул забезпечує обчислення 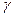в .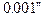

Знак зближення меридіанів співпадає зі знаком різниці довгот 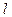або знаком 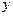, тобто для точок, які розташовані на схід від осьового меридіану, зближення меридіанів завжди буде додатнім, а на захід від нього - від’ємним.