Перетворення координат Гаусса-Крюгера із зони в зону.
Поділ поверхні еліпсоїда на меридіанні смуги певної ширини і зображення їх на площині у виді незалежних одна від другої координатних зон створює деякі труднощі в тих випадках, коли необхідно встановити геодезичний зв’язок між пунктами, координати яких задані в різних координатних зонах, тобто обчислені від різних осьових меридіанів.
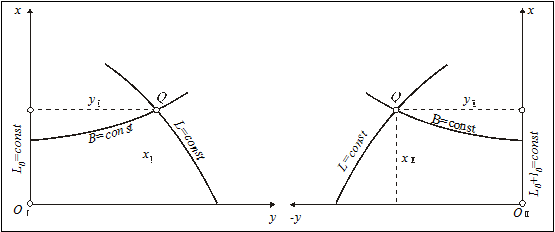
Нехай деяка точка 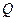 на еліпсоїді з координатами
на еліпсоїді з координатами  і
і 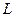 розміщена між осьовими меридіанами
розміщена між осьовими меридіанами 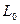 та
та  двох суміжних смуг (рис.4.9). Зображення її
двох суміжних смуг (рис.4.9). Зображення її 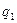 на площині, в проекції Гаусса-Крюгера, в системі координат західної зони (з осьовим меридіаном
на площині, в проекції Гаусса-Крюгера, в системі координат західної зони (з осьовим меридіаном 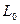 ) матиме координати
) матиме координати 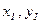 , а в системі координат східної зони (осьовий меридіан
, а в системі координат східної зони (осьовий меридіан  ) -
) - 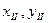 (рис. 4.9).
(рис. 4.9).
|
Рис.4.9
Якщо координати 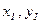 (чи
(чи 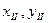 ) отримані в результаті опрацювання геодезичної мережі, в яку входить точка
) отримані в результаті опрацювання геодезичної мережі, в яку входить точка 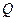 , то координати
, то координати 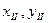 (чи
(чи 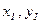 ) отримують відповідними обчисленнями на основі формул зв’язку між координатами
) отримують відповідними обчисленнями на основі формул зв’язку між координатами 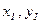 та
та 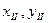 ; називають такі обчислення перетворенням координат.
; називають такі обчислення перетворенням координат.
В практиці геодезичних робіт потреба перетворювання плоских координат 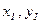 в координати
в координати 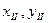 , тобто необхідність перейти від одної системи плоских прямокутних координат до другої, зустрічається доволі часто.
, тобто необхідність перейти від одної системи плоских прямокутних координат до другої, зустрічається доволі часто.
Наприклад, математичне опрацювання геодезичної мережі в системі плоских прямокутних координат Гаусса-Крюгера, пункти якої розміщені по обидві сторони від граничного меридіана сусідніх смуг на еліпсоїді, можливе тоді, якщо координати вихідних пунктів для цієї мережі будуть в одній системі плоских координат, тобто в одній координатній зоні.
При розв'язування оберненої геодезичної мережі на площині між пунктами, розміщеними в різних смугах на еліпсоїді плоскі координати повинні бути задані в одній координатній зоні.
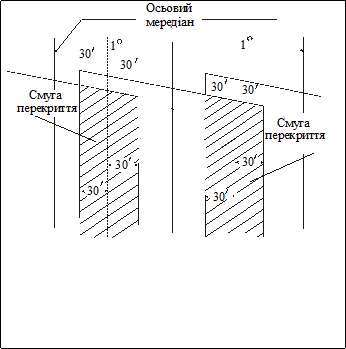
Для таких і їм подібних випадків, що нерідко зустрічаються на практиці, передбачено при створенні каталогів плоских прямокутних координат “перекриття” зон. Всі пункти, розміщені на 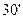 по довготі на схід і захід від граничного меридіана шестиградусних смуг в каталогах мають координати в двох зонах: відносно осьового меридіана
по довготі на схід і захід від граничного меридіана шестиградусних смуг в каталогах мають координати в двох зонах: відносно осьового меридіана 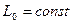 своєї зони і осьового меридіана
своєї зони і осьового меридіана 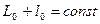 сусідньої зони. Схематично таке перекриття показано на рис.4.10. Цим, фактично, протяжність шестиградусних зон по довготі збільшується до
сусідньої зони. Схематично таке перекриття показано на рис.4.10. Цим, фактично, протяжність шестиградусних зон по довготі збільшується до 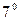 та створюється перекриття в
та створюється перекриття в 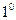 .
.
|
Рис.4.10
Проте перекриття зон не виключає всіх випадків обчислень на перетворення координат. Такі випадки можливі при проведенні топографо-геодезичних робіт на стику двох зон, як також і в одній зоні. В першому випадку виникає потреба перетворення координат із зони в зону, а в другому – переобчислення координат заданих в системі деякої стандартної зони відносно меридіана 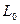 в місцеву систему координат відносно іншого меридіана з довготою
в місцеву систему координат відносно іншого меридіана з довготою 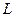 , прийнятого за осьовий.
, прийнятого за осьовий.
Загальна схема перетворення координат, коли задано 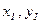 в одній зоні (з довготою осьового меридіана
в одній зоні (з довготою осьового меридіана 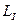 ), треба знайти
), треба знайти 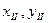 в другій зоні (з осьовим меридіаном
в другій зоні (з осьовим меридіаном 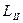 ):
):
1. Перехід від 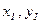 до
до  і
і  за формулами (4.20);
за формулами (4.20);
2. З врахуванням довготи 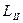 осьового меридіана другої зони перехід від
осьового меридіана другої зони перехід від  і
і 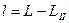 до
до 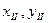 за формулами (4.15).
за формулами (4.15).
Можливим є безпосереднє перетворення плоских прямокутних координат одної зони в плоскі координати другої зони без проміжного переходу в геодезичні координати, тобто 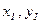

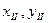 . Проте алгоритм і самі обчислення в цьому випадку, при відсутності допоміжних засобів в виді спеціальних таблиць, доволі громіздкі.
. Проте алгоритм і самі обчислення в цьому випадку, при відсутності допоміжних засобів в виді спеціальних таблиць, доволі громіздкі.
Числовий приклад.
Нехай задані плоскі прямокутні координати 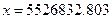 м ,
м , 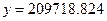 м деякого пункта в системі шестиградусної зони (
м деякого пункта в системі шестиградусної зони ( 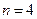 ) з осьовим меридіаном
) з осьовим меридіаном 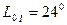 . Потрібно обчислити плоскі прямокутні координати цього пункта відносно осьового меридіана
. Потрібно обчислити плоскі прямокутні координати цього пункта відносно осьового меридіана 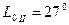 .
.
З заданими координатами 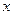 і
і 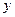 визначаємо геодезичні координати
визначаємо геодезичні координати  і
і 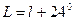 за формулами (4.20) з використанням (4.21). Тоді:
за формулами (4.20) з використанням (4.21). Тоді: 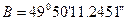 ,
, 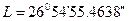 . Тепер, за відомими
. Тепер, за відомими  і
і 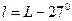 , використовуючи формули (4.15)-(4.17), знаходимо плоскі прямокутні координати відносно осьового меридіана
, використовуючи формули (4.15)-(4.17), знаходимо плоскі прямокутні координати відносно осьового меридіана 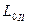 :
: 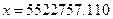 м і
м і 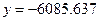 м.
м.
Дата добавления: 2015-07-24; просмотров: 1123;