Тема: Вычисление длины кривой, площади поверхности тела вращения.

9.1. Вычисление длины кривой.

9.1.1. Пусть некоторая кривая является графиком функции 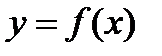, , 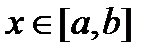для которой 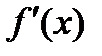является непрерывной функцией на 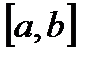. Такие кривые называются гладкими.

Во-первых, мы должны дать определение длины кривой, во-вторых, указать способ ее вычисления.

Отрезок 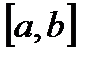произвольным способом разобьем на n частей точками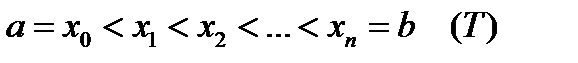

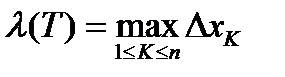
Этому разбиению будет соответствовать некоторое разбиение кривой AB на n частей точками .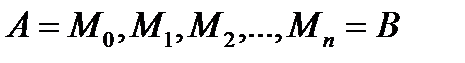

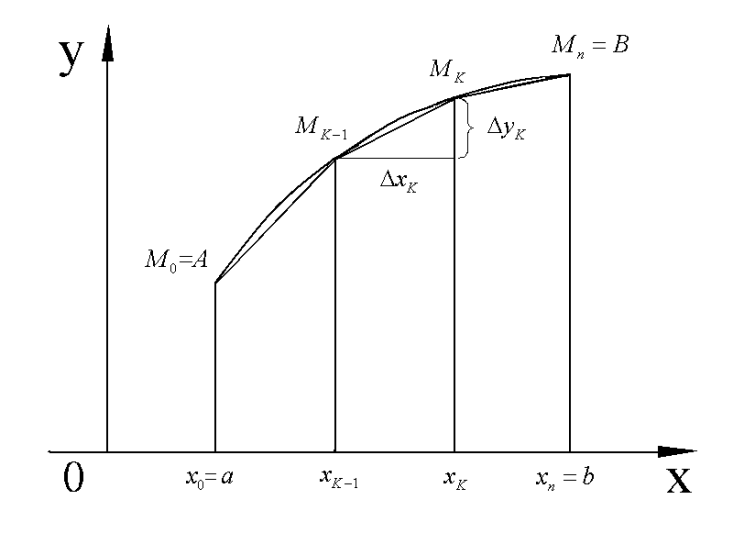
Соседние точки на кривой соединим отрезками, в результате получим ломаную 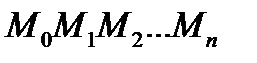. Длина К-того участка ломаной равна 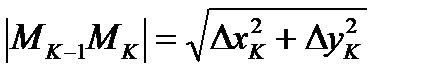, где .

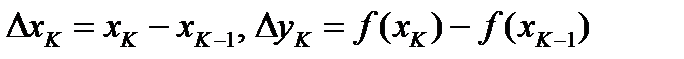Длина l данной кривой приближенно равна длине ломаной 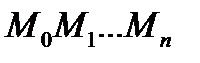, т.е. .

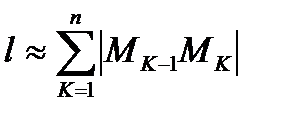За длину кривой принимают 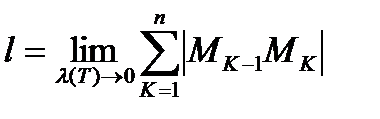. Кривая, имеющая длину называется спрямляемой. Вычислять длину кривой с помощью определения неудобно. Далее дадим способ вычисления длины кривой с помощью определенного интеграла.

Т.к. по условию непрерывна на 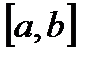, то 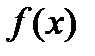тоже непрерывна на 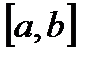. Поэтому 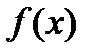на каждом из отрезков 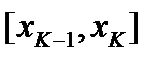удовлетворяет всем условиям теоремы Лагранжа, по которой .

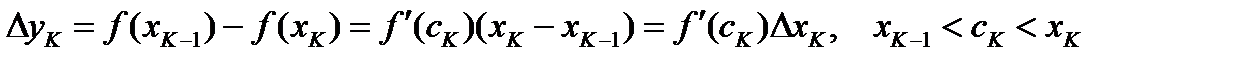Поэтому, .

.

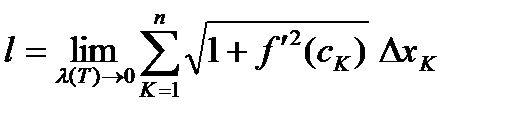Выражение под знаком предела является интегральной суммой для функции 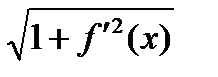. Следовательно,

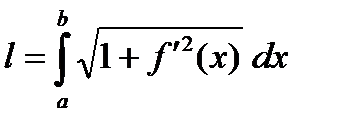. (1)

Мы предположили, что непрерывная функция на 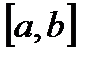, поэтому подынтегральная функция 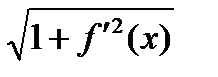непрерывна на 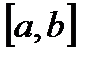и длина такой кривой существует, т.е. кривая спрямляема.

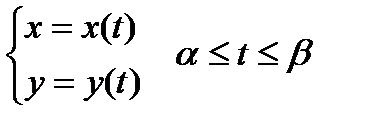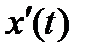9.1.2. Пусть уравнение кривой задано параметрически , где и 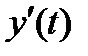непрерывны на 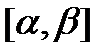, причем .

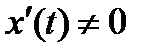Заметим, что в равенстве (1) выражение, стоящее под знаком интеграла, есть дифференциал длины кривой: 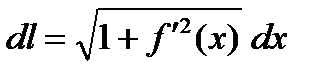. Дифференциал длины кривой, заданной параметрически, записывается в следующем виде:

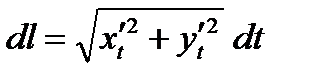, поэтому

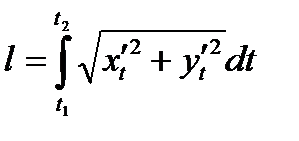(2)

9.1.3. Рассмотрим кривую, которая задана в полярной системе координат.

.

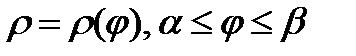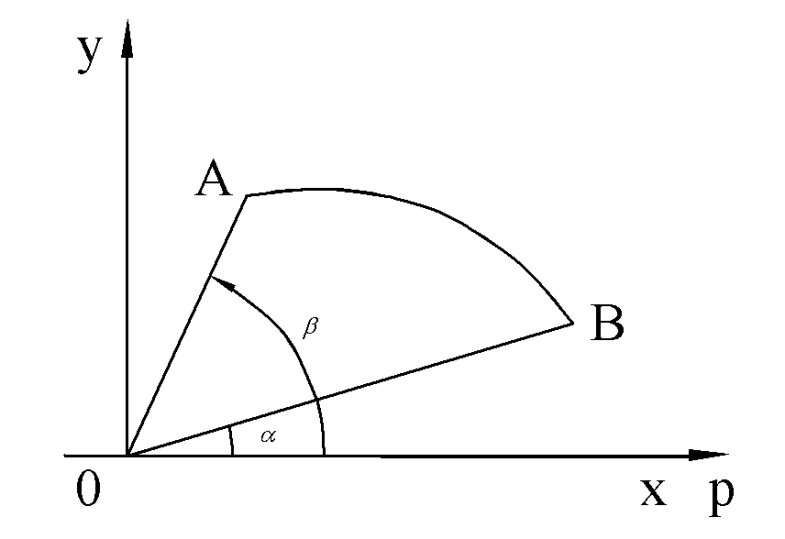
Напомним, что дифференциал дуги кривой в полярной системе координат имеет вид: 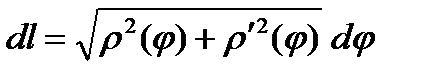, поэтому

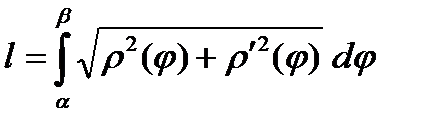. (3)

Пример. Вычислить длину кривой 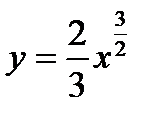от точки 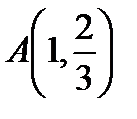до точки

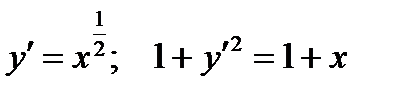
По формуле (1) получаем:

Пример. Вычислить длину одной арки циклоиды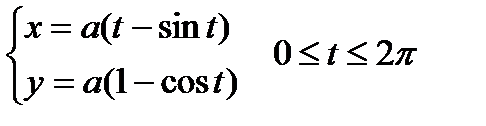

.

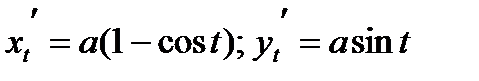
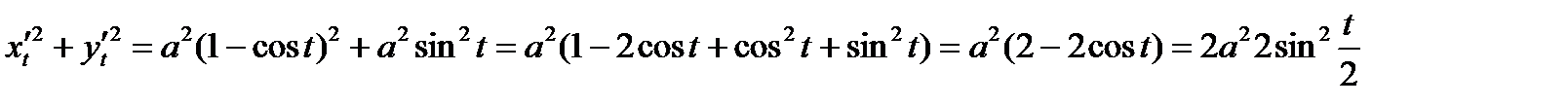По формуле (2) получаем

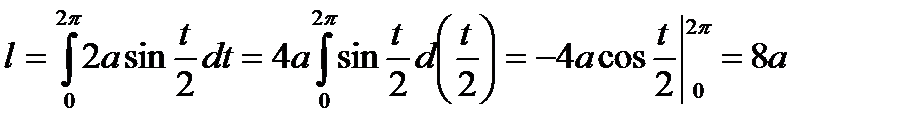
Пример. Вычислить длину кардиоиды

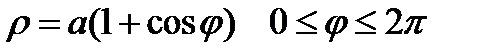
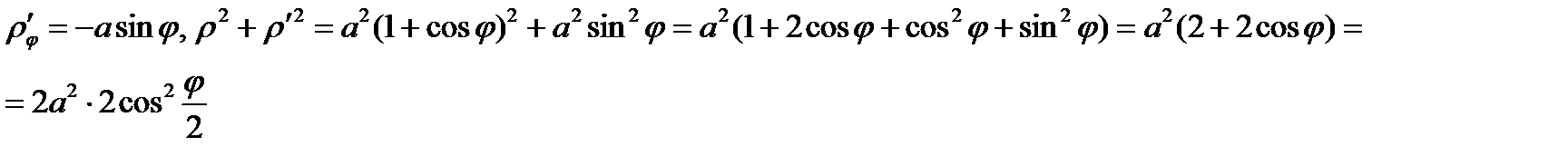
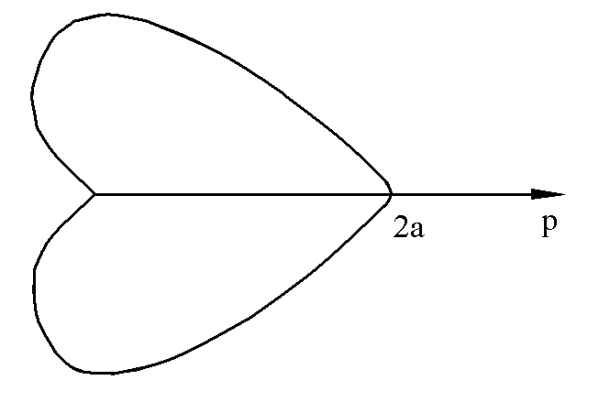
Т.к. кардиоида симметрична относительно поляры OP, то достаточно найти длину кардиоиды при 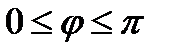, а затем удвоить.

.

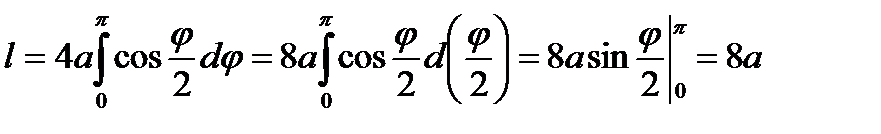9.2. Вычисление площади поверхности тела вращения.

Пусть кривая AB задана параметрически

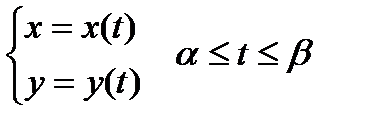, (4)

где 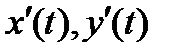непрерывны на отрезке 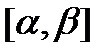. В этом случае кривая AB спрямляема, т.е. имеет длину, которую обозначим µ. Точка A имеет координаты 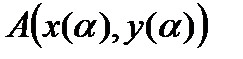. Рассмотрим на кривой AB точку M с координатами . Дуга AM спрямляема, т.к. вся кривая AB спрямляема. Пусть l(t) длина дуги AM. Функция l(t) возрастает с возрастанием t. Через t=t(l) обозначим обратную функцию. Подставляя это значение в уравнение (4), получим:

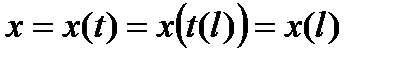(5)

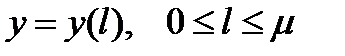, т.е. мы имеем параметрическое представление кривой, где за параметр принимается длина кривой l. Такое представление кривой бывает удобным во многих вопросах математики.

Пусть кривая AB задана уравнениями (5).

Дадим определение площади поверхности тела вращения.

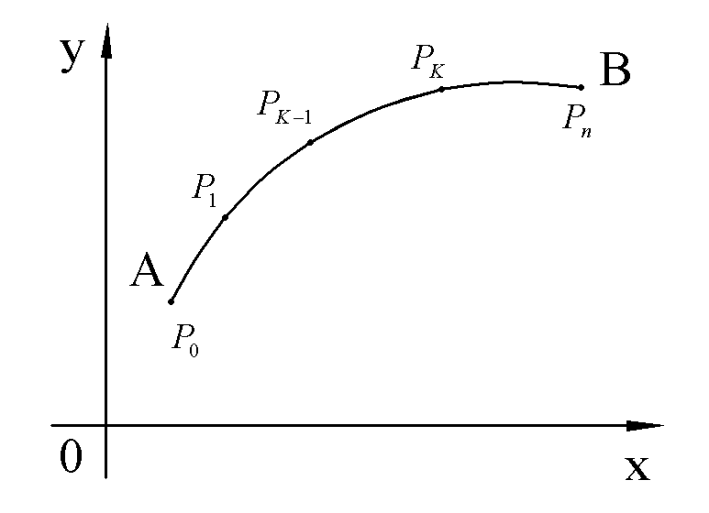
Отрезок 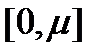произвольным способом разобьем на n частей точками

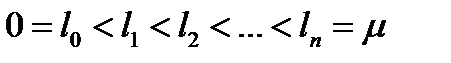
Это разбиение обозначим через (T). 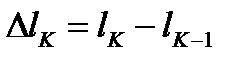, 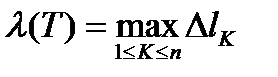. Точкам 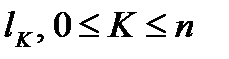, на кривой AB будут соответствовать точки 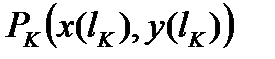. Полученные соседние точки соединим отрезками 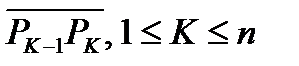, в результате получим ломаную 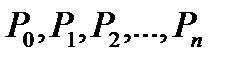. Через S(T) обозначим площадь поверхности вращения ломаной вокруг оси OX.

Определение. Площадью S поверхности вращения кривой AB вокруг оси OX называется предел площади S(T) при .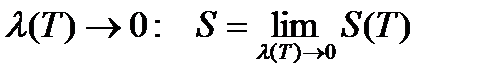

Далее выведем формулу, позволяющую вычислять площадь поверхности вращения с помощью определенного интеграла.

С этой целью подсчитаем площадь S(T). Через 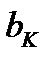обозначим длину отрезка 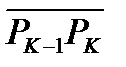. Поверхность вращения этого отрезка есть усеченный конус, радиусы основания которого равны 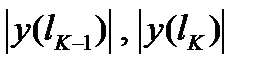, а длина образующей равна 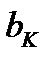. Следовательно, площадь поверхности К-того усеченного конуса равна

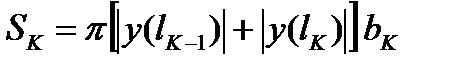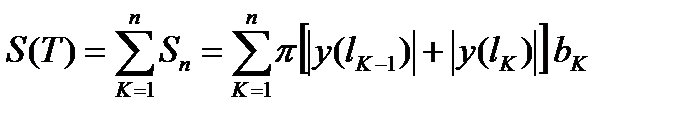, а (6)

Правая часть равенства (6) не является интегральной суммой, т.к. 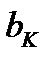не является приращением аргумента l.

Выражение для S(T) преобразуем следующим образом:

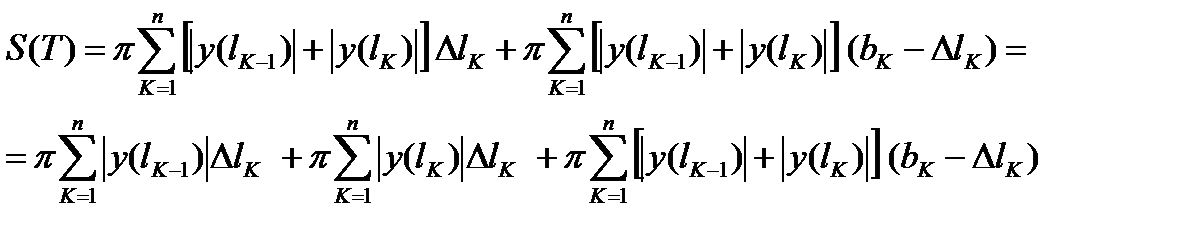(7)

Суммы 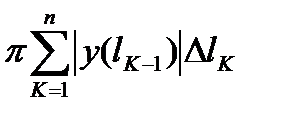, 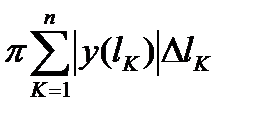являются интегральными суммами для непрерывной функции 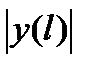. Поэтому

.

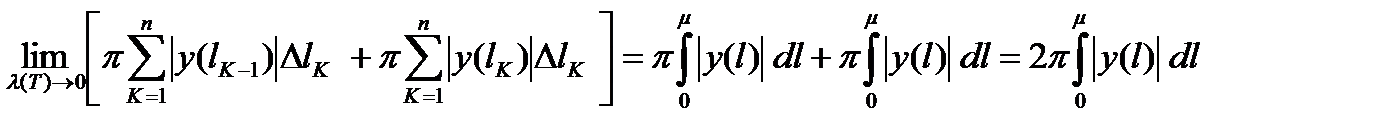Покажем теперь, что предел последней суммы в равенстве (7) равен нулю при 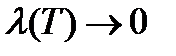. Функция 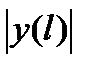непрерывна и поэтому она ограничена: .

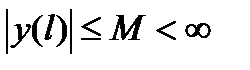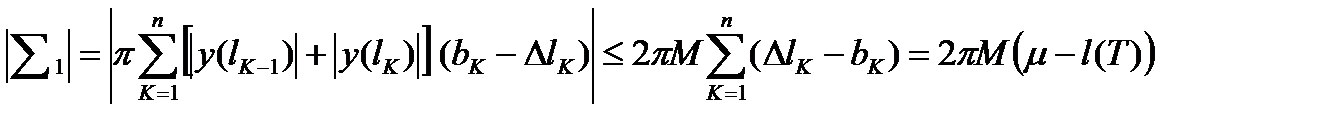, (8)

где µ - длина кривой, а l(T), как и ранее, длина ломаной.

Отсюда

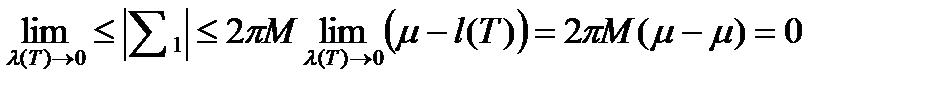(9)

Из равенств (7), (8) и (9) следует:

.

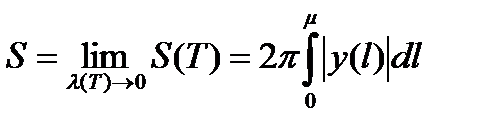Это и есть формула для вычисления площади поверхности вращения. При применении этой формулы надо найти длину кривой µ и найти функцию 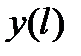, что представляет определенные неудобства.

Для получения формулы, свободной от этих недостатков, перейдем к исходному заданию кривой в параметрической форме (4). Под знаком интеграла сделаем замену переменной:

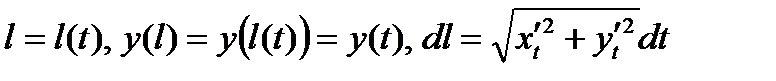, тогда будем иметь:

.

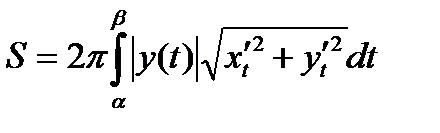В частности, если уравнение кривой задано в явном виде 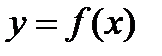, , 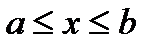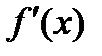- непрерывна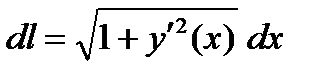, то , то

.

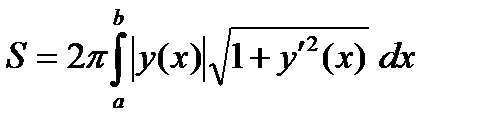Пример. Вычислить площадь S поверхности, образованной вращением одной арки циклоиды 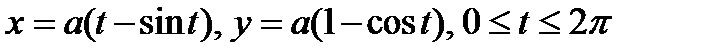, вокруг оси OX.

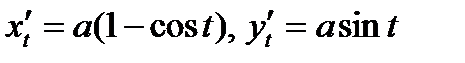
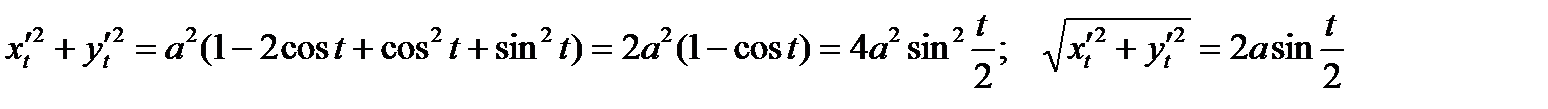
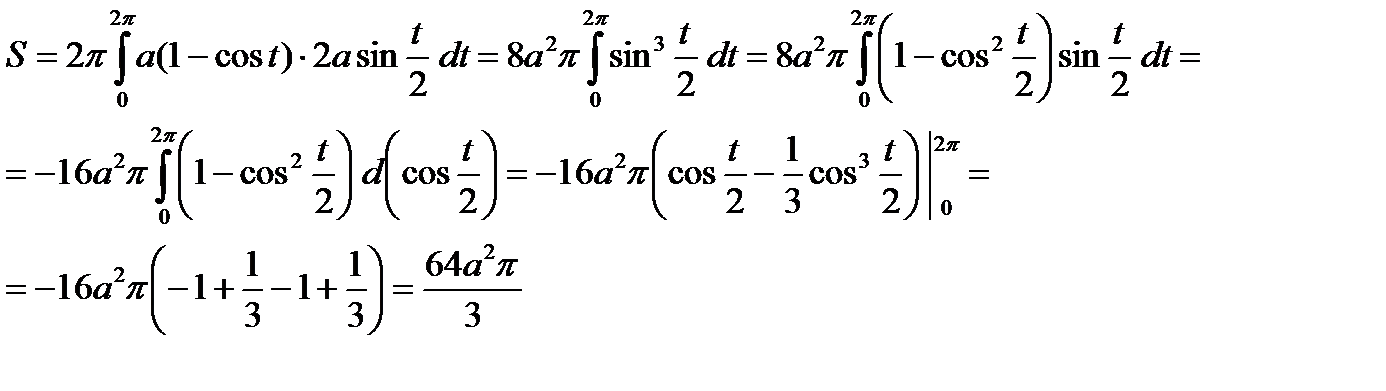
Пример. Вычислить площадь S поверхности, полученной при вращении кривой 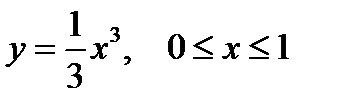, вокруг оси OX.

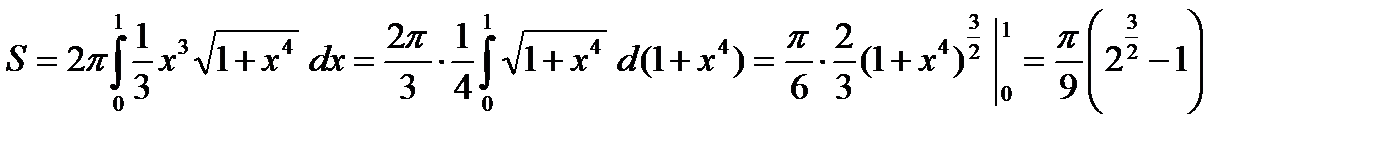
Пример. Вычислить площадь S поверхности, полученной при вращении кардиоиды 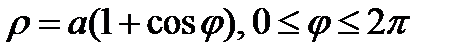, вокруг поляры OP.

В этом случае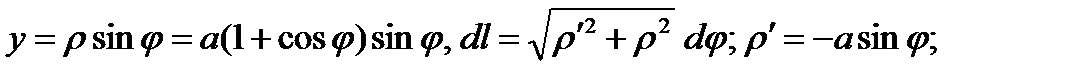

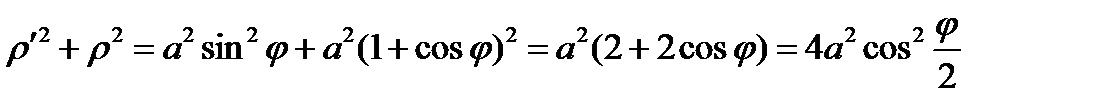
Нам достаточно взять половину кардиоиды при и вращать ее вокруг поляры OP.

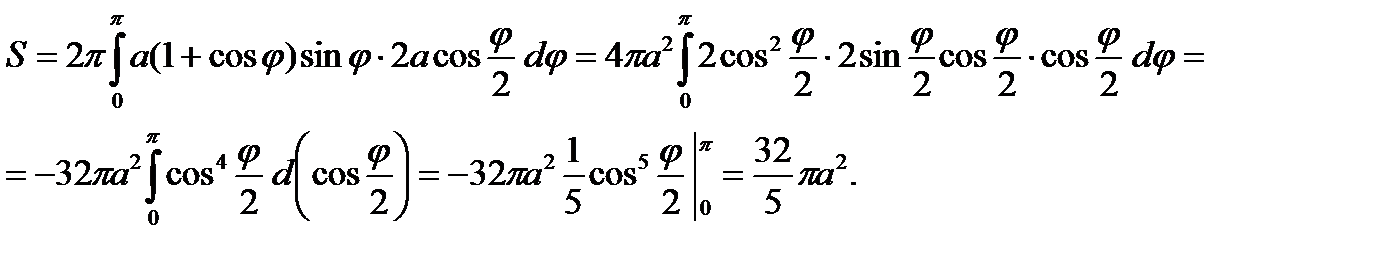
Литература:

1. Л.Д. Кудрявцев “Краткий курс математического анализа”, Москва, физматлит,2002 г., 400 с.

2. В.С. Зарубин и др. “Интегральное исчисление функций одного переменного” Москва, МГТУ им. Н.Э. Баумана, 1999 г., 528 с.

3. ”Сборник задач по математике для ВТУЗов” ред. А.В. Ефимов, Москва, физматлит, 2001 г., 485 с.