Анализ контактирования и оценка площади соприкосновения

При случайном расположении шероховатостей на поверхностях контактирующих тел контактное сближение этих тел под действием внешней нагрузки лимитирует фактическая площадь соприкосновения, определяемая геометрией контактирующих поверхностей.

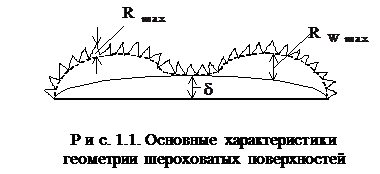
На рис. 1.1 показаны основные характеристики геометрии шероховатых поверхностей: шероховатость с максимальной высотой профиля Rmax, волнистость с максимальной высотой волны Rwmax и макроотклонения от горизонтальной базовой плоскости с размером δ.

Для оценки шероховатости используются: оптические, щуповые, электронно-микроскопические и другие методы. Промышленное применение приобрел щуповой метод. Суть его заключается в том, что по поверхности скользит игла с радиусом закругления 2-10 мкм, значительно меньшим, чем радиус закругления вершин микронеровностей. Колебания иглы в вертикальном направлении преобразуются в электрические сигналы, поступающие в микропроцессор, который выдает в цифровом виде основные характеристики профиля. В России профилографы серийно выпускает завод «Калибр», а за рубежом наиболее распространены приборы фирмы «Хьюлет-Паккард».

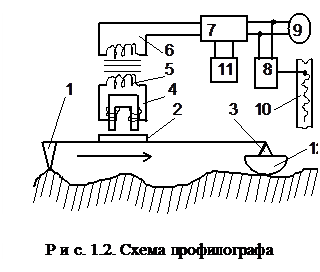На рис. 1.2 изображена схема современного профилографа. Игла 1 скользит по шероховатой поверхности и вместе с якорем 2 поворачивается относительно призмы 3, в результате чего меняется зазор между якорем 2 и сердечником 4, что генерирует переменный сигнал в катушках 5 и 6, который усиливается блоком 7 и регистрируется на ленте 10 самописца 8, а также стрелочным прибором 9. Микропроцессор 11 предназначен для вычисления стандартных показателей микрогеометрии, которые высвечиваются на цифровом табло. Для исключения влияния волнистости призма прибора прикреплена к шаровой опоре 12. Шаровая опора обеспечивает скольжение по вершинам микровыступов, огибая волны, поскольку если опора будет скользить по плоской гладкой поверхности, то одновременно будут записываться шероховатость и волнистость (см. рис. 1.1). Прибор позволяет изменять в широком диапазоне масштаб увеличения по осям Х и Y. Возможно увеличение по оси Y до 100000 раз.

В последние годы разработаны методы получения профилограмм на растровом, электронном и сканирующем (туннельном) микроскопах. Разрешение в этом случае достигает нанометров. Удается регистрировать шероховатость молекулярных размеров (субмикрошероховатость), а также микродефекты кристаллической структуры.

Рассмотрим основные характеристики микрогеометрии более подробно, в соответствии с действующим в России ГОСТ 2789-73.

Установленные этим стандартом характеристики шероховатостей иллюстрирует рис. 1.3. Основные из них высотные: R_a, R_z и R_max и шаг микронеровностей.

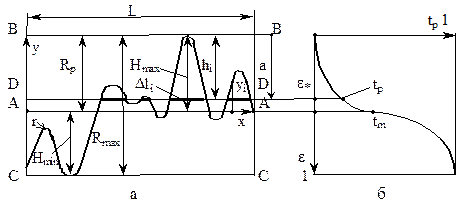
Р и с. 1.3. Характеристики шероховатостей

а) - характеристики шероховатостей; б) - опорная кривая.

Наиболее часто в технике применяют характеристику R_a - среднее арифметическое абсолютных значений отклонений профиля шероховатостей от средней линии в пределах базовой длины L:

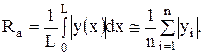(1.1.)

В формуле (1.1.) L - базовая длина, в пределах которой находится достаточно представительное число микронеровностей с точки зрения статистики; У_i - расстояние точки профиля от средней линии (см. рис. 1.3, а), n - число точек профиля, в которых измерено У_i. Положение средней линии АА находится из соображения о том, что она делит площадь профиля пополам 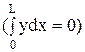. Профиль заключен между линиями выступов ВВ и впадин СС, которые проводятся через вершины самых высоких выступов и самые низкие точки впадин.

Параметр R_z - характеризует среднее расстояние между пятью высшими вершинами выступов и пятью низшими точками впадин:

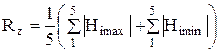. (1.2)

Расстояние между линиями выступов и впадин (R_max) равно толщине шероховатого слоя. Удаление линии выступов от средней линии обозначается R_p. Кроме перечисленных характеристик используются также средний шаг микронеровностей, средний угол наклона профиля, средний радиус закругления выступа.

По своей форме выступы напоминают пологие горные хребты. Угол при вершине для всех видов обработки обычно заключен в интервале от 150 до 176⁰. Наиболее близким по форме к реальному выступу является эллипсоид.

Обычно шероховатость имеет направленный характер, отражающий траекторию движения обрабатывающего инструмента. В связи с этим профилограммы снимают в продольном и поперечном направлениях. Средний радиус вершины выступа находят как среднегеометрическое из значений, измеренных в продольной и поперечной профилограммах:

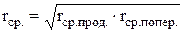. (1.3)

Для статистического анализа и представления характеристик шероховатых поверхностей используют закон распределения материала по глубине шероховатого слоя на выбранной базовой длине L, который характеризует опорная кривая (см. рис.1.3,б). Эту кривую получают как зависимость относительной суммы сечений микровыступов 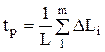от относительного сближения .

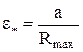Для аналитического описания опорной кривой используют степенную функцию. Так, начальный участок опорной кривой (см. рис. 1.3,б) принято описывать выражением

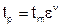. (1.4)

Здесь 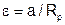, t_m=t_p при а=R_p, n>1 - параметры опорной кривой . Число выступов по мере удаления от верхней границы шероховатого слоя меняется по закону:

(1.5)

где n₀ - число выступов, вершины которых лежат выше средней линии.

Cтандартом предусмотрено 14 классов шероховатости. В табл.1.1. для примера приведены данные шероховатости наиболее ответственных деталей ДВС автомобилей.

Используя рассмотренные здесь стандартные характеристики, решают задачу оценки фактической площади контакта шероховатых поверхностей (ФПК).

На рис. 1.4 показана структурная схема площади контакта. Площадки фактического контакта DA_ri сгруппированы на площадях касания волн, совокупность которых составляет контурную площадь контакта DA_сi (КПК). Общая площадь со-

Таблица 1.1

Характеристики шероховатости

прикасания тел (кажущаяся), в пределах которой заключены ФПК и КПК, называется номинальной площадью контакта А_а (НПК).

Суммарная площадь фактического контакта

А_r= 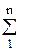DA_ri.

Наиболее полно методика расчета ФПК разработана профессором Н.Б. Демкиным (Тверской технический университет). В целях расчета ФПК шероховатость поверхности обычно моделируют набором сферических сегментов, вершины которых разбросаны по высоте таким образом, чтобы сохранить закон распределения материала в шероховатом слое, который задается с помощью полученной из опыта опорной кривой.

Рассмотрим по рис.1.5 контакт шероховатой поверхности с гладкой, что упрощает задачу, а результаты можно перенести на контакт двух шероховатых поверхностей. Поскольку в узлах трения деформация выступов невелика по сравнению с их размером, то можно пренебречь искажением формы и считать, что площадка контакта А_ri равна площади сечения выступа на расстоянии от вершины равном деформации а_i, которую называют сближением.

Рассмотрим сначала деформацию одного выступа (см. рис. 1.5). При упругой деформации ФПК и сближение рассчитываются по формулам Герца:

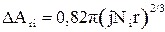; (1.6)

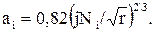(1.7)

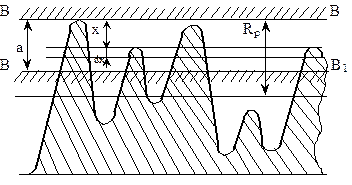
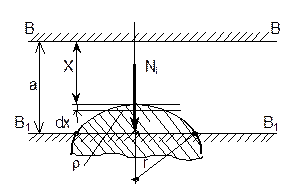
а б

Р и с. 1.5. К анализу оценки фактической площади контакта

Здесь 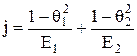- упругая постоянная; коэффициенты Пуассона; Е₁, Е₂ - модули Юнга для первой и второй поверхностей; N - нормальная нагрузка; r - радиус выступа. Если контактируют 2 сферических выступа, то r=r₁r₂/(r₁+r₂) - приведенный радиус кривизны выступов.

При пластической деформации возможно либо внедрение, либо расплющивание выступа. Среднее давление на контакте считается равным твердости более мягкого материала. Тогда:

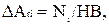(1.8)

a_i=N_i/2prHB . (1.9)

Здесь НВ - твердость по Бринелю, которая определяется как частное от деления нагрузки на площадь отпечатка, оставшегося после внедрения твердого шарика в пластичный материал. Формула (1.9) получается из геометрических соображений (см. рис.1.4,б):

r_i² = r² – (r - a_i)² @ 2a_ir; DA_ri = pr_i² @ 2pra_i , отсюда a_i@DA_ri/2pr@N_i/2prHB

Образное представление площади ФПК иллюстрируют с помощью следующего приема. Если мысленно срезать шероховатости на уровне, соответствующем части высоты выступов, то сумму образовавшихся площадок в сечениях выступов можно считать равной ФПК. ФПК вычисляют, пользуясь уравнением опорной кривой (1.4), что справедливо, когда площадь сечения выступа равна площади контакта, при условии, что сближение равно расстоянию от вершины до секущей плоскости. Так, примерно, и происходит при пластической деформации. Из формул (1.6), (1.7) следует, что при упругой деформации площадь сечения по средней линии DA_si связана с площадью контакта А_ri следующим образом:

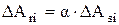, (1.10)

где коэффициент осадки 0,5 £ a £ 1. С учетом этого ФПК можно выразить через опорную кривую следующим образом:

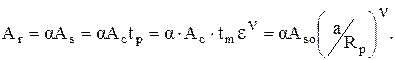(1.11)

Здесь учтено, что опорная кривая одинакова для профиля и поверхности, т.е. 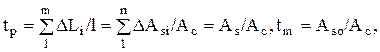A_so - сумма сечений выступов на уровне средней линии, A_c - контурная площадь контакта.

Прежде, чем приступить к расчету ФПК, проанализируем геометрию выступов шероховатости поверхностей. Для этого воспользуемся формулой (1.5) и рис.1.5.

Продифференцировав формулу (1.5), выразим число выступов, вершины которых лежат в слое dx (см. рис. 1.5,а):

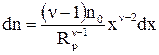. (1.12)

Из рис. 1.5,б выразим площадь сечения сферического выступа с вершиной в слое dx на уровне, удаленном на а от верхней границы:

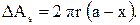(1.13)

Площадь сечения всех выступов, вершины которых лежат в слое dx на упомянутом уровне,

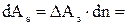
. (1.14)

Площадь сечения всех выступов, рассеченных плоскостью, удаленной от верхней границы на величину а

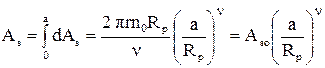. (1.15)

Это соответствует формуле (1.11) при a = 1. Следовательно, площадь сечения шероховатого слоя плоскостью, проходящей через среднюю линию,

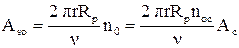. (1.16)

Здесь 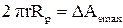- площадь сечения самого высокого выступа, 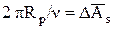- средняя площадь сечения выступов на среднем уровне; n_ос - число выступов, вершины которых расположены выше среднего уровня в расчете на единицу контурной площади (n_ос=n₀/A_c). Поскольку A_s0=t_m×A_c, то n₀=t_m×A_cn/2prR_p, n_oc= t_mn/2prR_p.

Идея расчета ФПК при упругом контактировании заключается в следующем. Шероховатый слой сжимается плоским гладким штампом от исходного положения ВВ до конечного В₁В (см. рис. 1.5). Каждый выступ деформируется на величину а-х. По формуле (1.7)

.

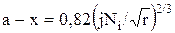Нагрузка на выступ, вершина которого лежит в слое dx,

.

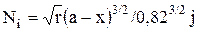Нагрузка, сжимающая все такие выступы, с учетом (1.12) равна

.

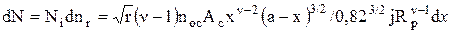Общая нагрузка на контакте

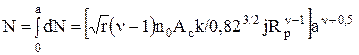. (1.17)

Здесь К=[1,5Г(n-1)Г(1,5)]/Г(n+1,5); Г- символ гамма-функции. Выразим из (1.17) сближение, и, подставив в формулу (1.15), с учетом (1.11), получаем выражение для ФПК:

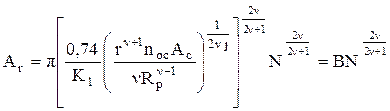. (1.18)

Здесь К₁=[1,5Г(n+1)Г(1,5)]/Г(n+1,5). Через формулу (1.17) выразим сближение:

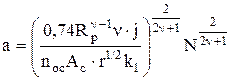. (1.19)

Формулы (1.18), (1.19) отражают влияние характеристик микрогеометрии, физико-механических свойств и нагрузки на показатели контактной деформации. Так, при изменении n от 2 до 3, что характерно для встречающихся на практике поверхностей, показатель степени нагрузки у A_r меняется от 4/5 до 6/7 . При увеличении n зависимость ФПК от нагрузки стремится к линейной.

При пластическом контакте среднее давление на пятнах касания близко к твердости по Бринелю, поэтому ФПК выражается в виде

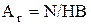. (1.20)

С учетом всего отмеченного, (см. формулы (1.11), (1.15) и (1.20) формула для вычисления сближения имеет вид

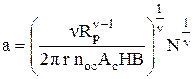. (1.21)

Отметим, что для приработанных поверхностей узлов трения характерен упругий контакт. Пластический контакт может частично проявиться при первых нагружениях, когда сжимаются наиболее высокие выступы. Последующие нагружения происходят уже в условиях, приближенных к упругому контакту. Пластический контакт имеет место также при обработке материалов резанием, ковкой, штамповкой, прессованием, накаткой и др.

Расчеты показывают, что с целью упрощения вычислений контакт двух шероховатых поверхностей можно приводить к контакту шероховатой и гладкой поверхностей, если вместо параметров n, t_m, R_max, r использовать эквивалентные значения, характеризующие обе поверхности:

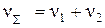; (1.22)

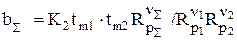; (1.23)

; (1.24)

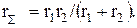(1.25)

Здесь .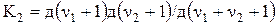

Индексы 1, 2 относятся к первой и второй поверхностям.

Если поверхности имеют ярко выраженную волнистость, то ее параметры определяют из волнограмм, снимаемых с помощью профилографов, и используют математическое описание, разработанное для шероховатого слоя. Контурную площадь контакта можно рассчитать по формуле

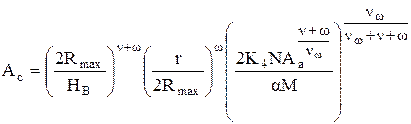. (1.26)

Здесь Н_в - наибольшая высота волны; А_а - номинальная площадь контакта; a и w - коэффициенты, равные при упругом контакте 0,5, а при пластическом 1 и 0 соответственно; n_w - параметр опорной кривой для волнистости; К₄ - постоянная интегрирования; М - характеристика механических свойств (при упругом контакте М=0,43j; при пластическом - М @ НВ).

Если волнистость выражена слабо (Нв £ Rmax), то ею можно пренебречь и считать в формулах (1.18), (1.19), (1.21) А_с=А_а.

Отдельно остановимся на формировании ФПК резин, поскольку они широко используются в узлах машин и механизмов и, в особенности, в автотранспортных средствах. Резины, независимо от природы (на основе натуральных или искусственных каучуков), имеют чрезвычайно низкий модуль упругости (порядка 5-30 МПа). Коэффициент Пуассона у них близок к 0,5, следовательно, даже при небольших давлениях они подчиняются закону Паскаля, ведут себя как жидкости. В отличие от твердых тел, уже при давлении порядка значения модуля упругости, фактическая площадь контакта у них приближается по величине к номинальной площади. На рис.1.6 показан примерный график зависимости ФПК от номинального давления.

Величину ФПК можно рассчитать по уточненной формуле Бартенева Г.М. - Лаврентьева В.В.:

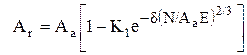, (1.27)

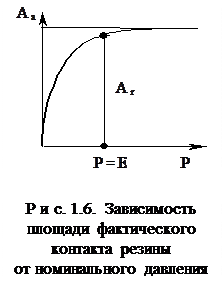где - K₁=0,8 ¸ 1; d @ 1,2(ar/R_z)^1/3; a = n₀/n_m, n_m - число оснований выступов в расчете на единицу номинальной площади контакта; Е - модуль упругости резины; n_o - число выступов, пересеченных средним уровнем.

Приведенные формулы для расчета ФПК не учитывают влияния времени действия нагрузки и температуры. Все материалы в большей или меньшей степени обладают вязкоупругостью и вязкопластичностью, т.е. упругая и пластическая деформации возникают не мгновенно после нагружения, а развиваются во времени. Скорость нарастания деформации увеличивается с повышением температуры. Такое поведение материалов, приводящее к изменению ФПК в зависимости от температуры и времени, описывается с помощью реологических моделей в рамках науки реологии. На рис. 1.7,а,б,в представлены простейшие модели, описывающие отдельные стороны поведения материалов.

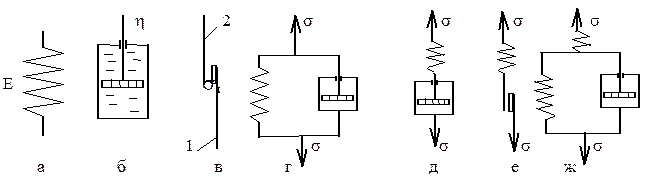
Р и с. 1.7. Реологические модели

Первая модель (см. рис.1.7,а) характеризует идеальную упругость (тело Гука).

Для нее связь между напряжением (s) и деформацией (e) дается законом Гука:

s = e E . (1.28)

Вторая модель (см. рис.1.7,б) отражает вязкое течение (тело-Ньютона). Для нее применима формула Ньютона:

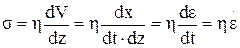. (1.29)

Здесь 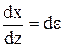- относительная деформация сдвига.

Третья модель (см. рис.1.7,в) характеризует переход к пластической деформации (тело Сен-Венана):

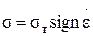, (1.30)

где sign - обозначение ступенчато изменяющейся функции. Если s > s_т , то элементы 1, 2 являются одним целым (e = 0), если s > s_т - элементы скользят относительно друг друга, тело неограниченно пластически деформируется (e®¥). Далее следуют комбинации из первых трех моделей (см. рис.1.7,г,д,е), отражающие в первом приближении свойства реальных тел. Первой (г) является модель Кельвина-Фойгта, учитывая, что общее напряжение здесь воспринимается телами Гука и Ньютона:

. (1.31)

Считая s=const и интегрируя, получаем закон развития деформации во времени:

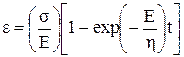. (1.32)

Если в какой-то момент времени t тело разгрузить (s=0), то интегрируя уравнение (1.31), получим закон снижения деформации во времени:

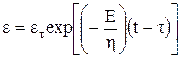. (1.33)

Отношение 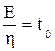называют временем релаксации.

Для модели Максвелла (Д) при приложении нагрузки сначала мгновенно деформируется тело Гука, а затем вступает в действие тело Ньютона. Поскольку тела соединены последовательно, то напряжения у них одинаковы. Скорость деформации системы складывается из скоростей для обоих тел:

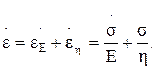(1.34)

Если принять, что e = const , интегрируя, получаем закон снижения напряжения во времени:

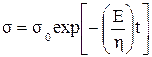, (1.35)

где s₀ - напряжение в начальный момент. Обе модели (см. рис.1.7,г,д) характеризуют поведение вязкоупругих тел.

Модель Прандтля -е характеризует поведение вязкопластичных тел.

Для нее 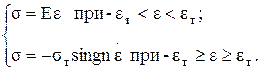(1.36)

Здесь 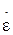- упругая деформация при s=s_т , s_т - предел текучести. Пока s < s_т , деформируется только тело Гука. Как только s³s_т , деформация неограниченно нарастает из-за проскальзывания тела Сен-Венана при постоянной деформации упругого элемента. На рис. 1.8. изображены реологические кривые для моделей Кельвина-Фойгта, Максвелла и Прандтля. Однако поведение реальных материалов в зоне контакта оказывается обычно сложнее, чем для рассмотренных моделей, поэтому приходится создавать более сложные композиции. В качестве примера на рис. 1.7,ж приведена модель, использованная в работах А.Ю. Ишлинского и И.В. Крагельского для объяснения зависимости силы трения от скорости скольжения.

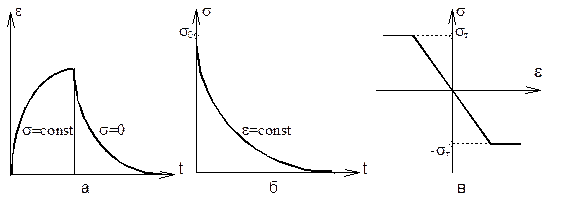
Р и с. 1.8. Реологические кривые

Влияние температуры и времени на ФПК наиболее заметно проявляется при пластическом контакте. Рост ФПК при повышении температуры в основном обусловлен снижением твердости, происходящим по экспоненциальному закону. Временная зависимость ФПК при постоянной нагрузке для металлов удовлетворительно описывается формулой

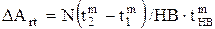, (1.37)

где DА_rt - изменение ФПК за промежуток времени t₂-t₁, t_HB - время выдержки под нагрузкой шарового наконечника при определении твердости по Бринелю, m - реологическая постоянная материала.

Вкратце рассмотрим экспериментальные методы измерения ФПК. Все методы можно разделить на 2 группы: методы, основанные на изучении оттиска поверхности, и методы, основанные на прямом или косвенном измерении площади в условиях контактирования. Первая группа методов легче реализуется, но требует нарушения контакта. Сюда относятся методы измерения с использованием индикаторных пленок люминофоров, радиоизотопов, красящих веществ, наносимых на одну из контактирующих поверхностей. Поверхности после контактирования разнимают и с помощью планиметра измеряют площадь пятен. Все методы имеют индивидуальные источники погрешностей. Наиболее точные результаты дают 3 метода: метод угольных пленок, метод оценки переноса атомов материала одной поверхности на другую и метод измерения площадок сжатия выступов при контакте шероховатого тела с гладким.

Первый метод наиболее прост и доступен. На поверхность одной из деталей пары, покрытой тончайшим слоем смазки, напыляется в низком вакууме тонкая (толщиной до 1 мкм) пленка угля. Затем на напыленную поверхность накладывают вторую деталь пары и сжимают их приложением нормальной нагрузки. В местах контакта пленка разрушается, и светлые пятна касания отчетливо видны на черном фоне. Их площадь легко измерить планиметрированием. Второй метод заключается в обследовании побывавшей в контакте поверхности на растровом электронном микроскопе с рентгеновским микроанализатором, который настраивается на материал контртела. Анализатор регистрирует пятна контакта, как совокупность перенесенных при взаимодействии атомов контр-тела. Третий метод основан на измерении площадок смятия выступов металлических шероховатых тел после их контактирования с плоской твердой гладкой поверхностью. Площадки видны, как зеркальные пятна на сером фоне. Измерения проводятся в автоматическом режиме с использованием телевизионных планиметров. Метод применим только в условиях пластического контакта.

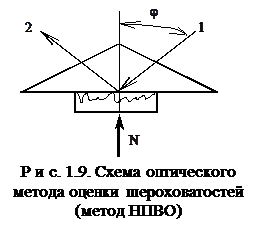Вторая группа методов позволяет измерять ФПК в условиях взаимодействия поверхностей. К ней относится метод нарушения полного внутреннего отражения (НПВО). Схема метода показана на рис. 1.9. Луч света 1 падает под углом, большим предельного, на грань прозрачной призмы и испытывает полное внутреннее отражение. К призме прижимается шероховатое тело. В местах контакта полное внутреннее отражение нарушается, и пятна контакта в лучах отраженного света 2 выглядят темными на светлом фоне. Применение метода ограничено узким выбором прозрачного материала, в качестве которого обычно используется стекло, обладающее низкой прочностью.

Другим методом является измерение электросопротивления контакта, по которому можно рассчитать ФПК. Здесь главным источником погрешности является наличие на поверхностях пленок окислов, проводимость которых много меньше, чем у металлов.