Трение скольжения

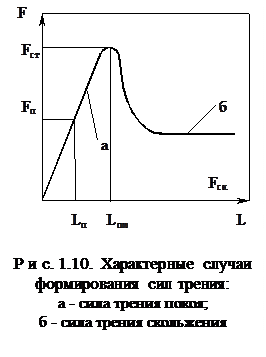
Под трением понимают сопротивление, возникающее при перемещении одного тела относительно другого, прижатого к первому. При этом различают трение покоя, скольжения и качения рис. 1.10.

Силой трения покоя (F_n) называют сдвиговое усилие, прикладываемое к контактирующим телам, и не вызывающее их взаимного скольжения (см. рис. 1.10,а). При этом взаимное перемещение (L_n) достигается за счет деформации материала выступов шероховатости в зоне контакта и называется предварительным смещением. Оно носит в основном упругий характер и исчезает при снятии сдвигающего усилия. Однако по мере роста сдвигающего усилия предварительное смещение приобретает пластический характер и становится частично необратимым. На рисунке показана предельная величина предварительного смещения (L_пм) и соответственно предельное значение силы трения покоя, которое называют статической силой трения. При дальнейшем увеличении перемещения начинается скольжение.

Силу трения можно представить в виде произведения удельной силы трения (t) и фактической площади контакта (А_r):

F = tA_r. (1.38)

Под коэффициентом трения понимают отношение силы трения к действующему на контакте нормальному усилию:

m = F/N. (1.39)

Здесь также различают коэффициенты трения покоя (статический) и скольжения (кинетический).

В зависимости от характера смазочной прослойки различают 4 вида трения: сухое, граничное, гидродинамическое (жидкостное) и смешанное (одновременно имеются элементы сухого, граничного и гидродинамического трения). В первом случае контактируют несмазываемые поверхности, покрытые окисными пленками и тончайшими слоями молекул газов и воды, адсорбированными из окружающей среды. Во втором случае, помимо перечисленных пленок, присутствуют молекулы смазочных материалов в виде тонкого слоя толщиной в несколько молекул, которые прочно связаны с поверхностью. В третьем случае слой жидкой смазки полностью разделяет сопряженные поверхности.

Сухое и граничное трения сходны по своей природе и имеют общие закономерности. Причиной служит то обстоятельство, что при граничном трении мономолекулярные слои смазки прочно связаны с твердой поверхностью, обладают твердообразными свойствами и как бы служат продолжением твердой фазы. Поэтому, как и при сухом трении, фактически имеет место контакт двух твердых поверхностей. Отличие проявляется в разных значениях коэффициента трения. Если при сухом трении он обычно больше 0,2 , то при граничном его величина заключена в интервале 0,05-0,2.

Механизм возникновения трения объясняет молекулярно-механическая теория трения, в разработку которой внесли большой вклад российские ученые (Б.В. Дерягин, И.В. Крагельский и др.) и зарубежные (Боуден, Тейбор, Томлинсон и др.). В соответствии с этой теорией трение имеет двойственную молекулярно-механическую природу. Силу трения можно представить как сумму молекулярной (адгезионной) и механической (деформационной) составляющих:

F = F_A + F_D . (1.40)

Молекулярная составляющая обусловлена сопротивлением разрыву молекулярных либо межатомных связей, которые возникают между контактирующими телами. Механизм этого процесса аналогичен описанному в гл. 2 для разрушения кристаллической решетки при сдвиге. Рассеяние работы трения в теплоту связано с упругой деформацией кристаллических решеток. Работа внешней силы переходит в потенциальную энергию решеток. После разрыва связи потенциальная энергия переходит в энергию колебаний атомов - во внутреннюю.

Механическая составляющая вызвана сопротивлением упругому и пластическому оттеснению выступов контактирующих тел, внедрившихся при движении в контроповерхности (см. рис. 1.11).

На рис. 1.11,а показано скольжение жесткого сферического выступа по вязкоупругому полупространству. Материал после прохода выступа из-за запаздывания деформации по отношению к нагрузке не успевает восстанавливать форму. Поэтому выступы перед индентором и после несимметричны, а реакция опоры, приложенная в центре контактной поверхности, не совпадает по направлению с нормальным усилием . Это явление характеризуется гистерезисом деформации. На рис. 1.12 показана кривая гистерезиса при растяжении-сжатии вязкоупругого стержня. Кривая ОМ отражает процесс нагружения, а кривая MN - процесс разгрузки. Из-за запаздывания деформации в тот момент, когда напряжение равно нулю, деформация не исчезает и равна e_о. Поэтому след, оставшийся при движе 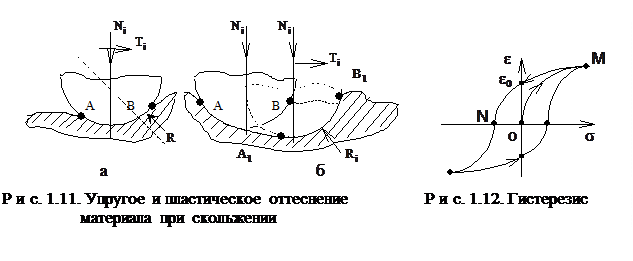нии выступа, не успевает восстанавливаться полностью, чего следовало бы ожидать для идеальной упругой среды.

На рис. 1.11,б показано поведение жесткого выступа при скольжении по пластической среде. В начале, пока скольжение отсутствует, под действием нормального усилия выступ заглубляется. Контактная кривая АВ симметрична. При скольжении задняя граница выступа отрывается от лунки. Вся нагрузка сосредотачивается на передней границе, а дуга контакта занимает положение А₁В₁. Впереди возникает валик оттесняемого материала. Реакция опоры не совпадает по направлению с нормальным усилием.

Поскольку молекулярное и механическое взаимодействие осуществляется на ФПК, то сила трения выраженная формулой (1.40) записывается в виде

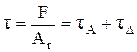, (1.41)

где t_A, t_D - адгезионная и деформационная составляющие удельного усилия.

Многочисленные попытки вывести расчетное соотношение для адгезионной составляющей (t_A) не увенчались успехом из-за невозможности учесть влияние пленок вторичных структур, покрывающих поверхности. В то же время для ювенильных металлических поверхностей установлено, что при их контакте решетки материалов обеих поверхностей сращиваются (холодная сварка), и удельная сила трения близка к сопротивлению сдвигу решетки. Последние исследования показали, что на физических площадках контакта, обусловленных смятием субмикронеровностей, сопротивление сдвигу контактирующих кристаллов приближается к теоретической прочности. Однако для реальных поверхностей, покрытых пленками, адгезионная составляющая значительно ниже. Работы Б.В. Дерягина, И.В. Крагельского, Н.М. Михина и др. показали, что зависимость адгезионной составляющей удельной силы трения от фактического давления (s_r=N/A_r) выражается в виде двучленного закона:

t_A=t₀ + bs_Г , (1.42)

где t₀ и b - молекулярные константы трения, определяемые экспериментально. Для определения этих констант Н.М. Михиным и К.С. Ляпиным разработан специальный прибор - тангензиометр, схема которого представлена на рис. 1.13.

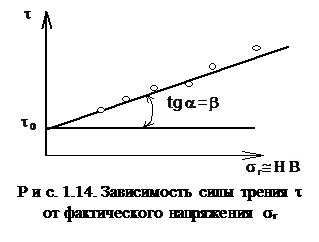
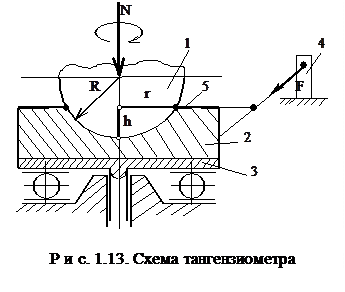Сферический индентор 1 внедря-ется в образец 2 на глубину h. Образец прикреплен к установленной в подшипнике подставке 3. Индентор приводится во вращение и за счет трения увлекает за собой образец 2. Однако образец удерживается от вращения пружиной 4, с которой он связан. Пружина служит для измерения момента трения. По величине момента рассчитывается удельная сила трения. Для этой цели измеряется радиус лунки (r). Фактическое давление вычисляют как отношение нормального усилия к площади отпечатка. Для того, чтобы площадь отпечатка равнялась ФПК, в качестве индентора используют шарики, поверхность которых является зеркально гладкой, а поверхность образца подвергают тщательной полировке. При использовании этого метода возникает затруднение, заключающееся в том, что фактическое давление равно твердости. Следовательно, для данного образца можно получить только одно значение удельной силы трения. Для получения зависимости необходимо, чтобы твердость изменялась в широком диапазоне. Это достигается за счет применения 5-6 образцов из материалов с разной твердостью. Испытуемый материал 5 наносится на эти образцы в виде гальванического покрытия либо в виде фольги, прочно прикрепляемой к поверхности образца. Такой прием позволяет получить зависимость t(s_r), вид которой показан на рис. 1.14.

Обрабатывая результаты измерений, определяют молекулярные константы t₀ и b.

Из формулы (1.40) видно, что адгезионную составляющую силы трения можно представить в виде

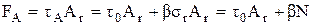. (1.43)

Адгезионная составляющая коэффициента трения

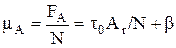. (1.44)

Если деформация выступов упругая, то, подставляя выражение ФПК из формулы (1.18) в формулу (1.44), получаем

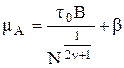. (1.45)

С повышением нормального усилия коэффициент трения убывает. Для пластического контакта, используя формулу (1.20) получаем

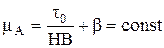. (1.46)

Коэффициент трения не зависит от нагрузки.

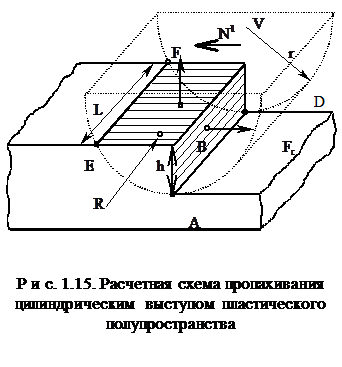Рассмотрим механическую составляющую на примере пропахивания цилиндрическим выступом пластического полупространства (см. рис. 1.15).

Цилиндрический выступ заглублен на h в полупространство. Реакция со стороны оттесняемого материала

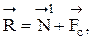
где N^l - вертикальная составляющая равна нормальной нагрузке; F_C - горизонтальная составляющая равна механическому сопротивлению. Поскольку деформация пластическая, то

N^l@S_BCFE×HB; F_c@S_ABCD×HB .

Коэффициент трения (механическая составляющая)

m_D = F_C/N^l = S_ABCD/S_BCFE ;

E@ 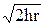; S_BCFE=BE×L; S_ABCD=hL.

Таким образом, для цилиндрического выступа 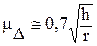, для сферического выступа .

При переходе к множественному контакту силу трения находят в виде суммы сил по всем контактирующим выступам:

.

Проведя такую операцию для пластического контакта, получаем

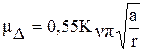, (1.47)

где а - сближение поверхностей при скольжении,

Для вязкоупругого контакта

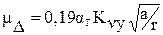, (1.48)

где 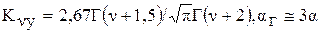- коэффициент гистерезисных потерь в условиях трения; a - коэффициент гистерезисных потерь, измеренный при циклическом растяжении-сжатии стержня. Коэффициент гистерезисных потерь вычисляется как доля рассеянной в теплоту энергии за деформационный цикл. Величина a_г для металлов невелика (0,02-0,04) и значительно выше для пластмасс и резины (0,08-0,2).

Многочисленные исследования показали, что для металлов деформационная составляющая коэффициента трения примерно в 100 раз меньше, чем адгезионная. Поэтому коэффициент трения в первом приближении равен адгезионной составляющей. Несколько иначе дело обстоит для пластмасс и резин. В последнем случае различие снижается более, чем на порядок, и, если резина скользит по грубо обработанной поверхности, деформационной составляющей пренебрегать не следует.

Важной особенностью резин является быстрое насыщение площади контакта при сравнительно низкой нагрузке (см. рис. 1.6). Благодаря высоким значениям (К_vу) при низком номинальном давлении коэффициент трения резин велик и может превышать единицу. Однако с ростом давления он быстро снижается, особенно, когда ФПК становится равна НПК и при давлении порядка 50-100МПа составляет 0,05-0,02.

Для измерения силы трения применяют различные трибометры. На них изучают трение образцов в виде дисков, контактирующих торцами; цилиндров, контактирующих по образующей, и т.д. Наиболее простым и часто используемым является трибометр, схема которого изображена на рис. 1.16.

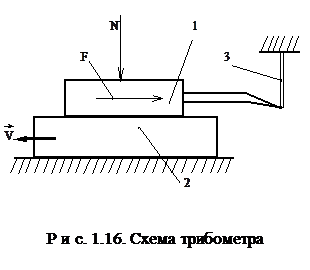Образец 1 прикрепляется к пружинному динамометру 3 и прижимается к контртелу 2, приводимому в движение. Динамометр измеряет силу трения. Прибор позволяет исследовать влияние на трение шероховатости поверхностей, материалов пары трения, нормальной нагрузки, скорости скольжения, температуры, смазки и многих других факторов.