Трение качения

Если бы колесо, катящееся по основанию, не испытывало проскальзывания, то такое движение было бы чистым качением и путь, проходимый любой точкой поверхности колеса по основанию за один оборот, составлял бы 2pr. Однако качения без проскальзывания не бывает. Колесо и основание испытывают упругие деформации. При этом колесо в зоне контакта сжимается, а основание - растягивается (стрелки на рис. 1.19,а).

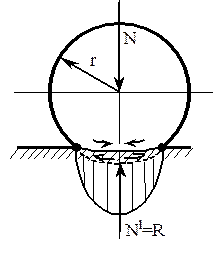
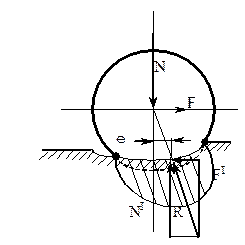
а б

Р и с. 1.19. Взаимодействия колеса с опорой

Поэтому на контакте постоянно происходит проскальзывание колеса относительно основания. Это один из источников рассеяния энергии. Другим источником является вязкоупругое поведение материалов основания колеса. Если к оси колеса не приложено тяговое усилие, то дуга контакта симметрична (см. рис. 1.19,а), и реакция опоры соосна с нормальной нагрузкой. Если приложить тяговое усилие и колесо приходит в движение, то зона контакта искажается (см. рис. 1.19,б). Материал сзади колеса не успевает восстановить форму. Эпюра давлений смещается в сторону движения. Большая часть дуги контакта оказывается во фронтальной части. Реакция опоры распределяется на 2 составляющих: вертикальную ( 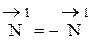) и горизонтальную (F^l) которая представляет собой сопротивление перекатыванию.

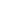Поскольку из условия равновесия 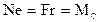, то коэффициент трения качения

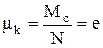, (1.52)

где e - эксцентриситет - смещение центра опорной поверхности от вертикали (см. рис. 1.19,б). Наряду с этой характеристикой используется коэффициент сопротивления качению, равный отношению работы на единичном пути к нормальной нагрузке. Работа при повороте на угол dj равна Mdj, а пройденный путь - Dl = rdj. Тогда коэффициент сопротивления

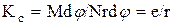. (1.53)

Это выражение было получено Кулоном. Дальнейшие исследования показали, что эксцентриситет не является константой и 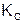~1/rⁿ, причем n<1.

Далее было установлено, что проскальзывание вносит незначительный вклад в потери энергии, а главный источник потерь - вязкоупругие деформации катка и опоры. Рассеивание энергии связано в основном с гистерезисом деформации. Исходя их этих соображений, для цилиндрического катка

m_k =0,24a_r (q×r×j)^1/2, (1.54)

где q - нагрузка, приходящаяся на единицу длины. Более детально задача о качении жесткого цилиндра по вязкоупругому полупространству решена академиком А.Ю. Ишлинским. Свойства полупространства описаны реологической моделью Кельвина-Фойгта (см. рис. 1.7,г). Для малых скоростей качения

m_k=C₁V, (1.55)

а для больших скоростей

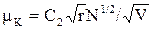. (1.56)

При малых скоростях коэффициент трения качения увеличивается с повышением скорости, а при больших - уменьшается.

Дальнейшее развитие теория трения качения получила в работах И.Г. Горячевой, которая рассмотрела качение вязкоупругих тел при наличии на площадке контакта зон сцепления и проскальзывания. Она показала, что в случае одинаковых материалов зона сцепления располагается на фронтальной части дуги контакта, а проскальзывание - на тыльной.