Узел трения как объект моделирования в динамике машин

Вибрация, удары, сложные процессы переноса механических возмущений в узлах и механизмах машин являются объектом изучения научной дисциплины, именуемой «Динамика машин». В России основы этой науки в применении к узлам трения заложены такими учеными, как Н.Н. Давиденков, А.С. Ахматов, Д.М. Толстой, К.В. Фролов, В.А. Кудинов и др.

Рассмотрим некоторые основные понятия и термины динамики машин, необходимые для динамического анализа узлов трения.

Понятие «узел трения». В триботехнике принято рассматривать узлы трения как механизмы или составляющие машин, в которых имеет место относительное движение соприкасающихся частей.

Узлами трения являются подшипники скольжения и качения, прямолинейные и цилиндрические направляющие, ползуны, зубчатые, фрикционные механизмы и др.

Понятие «динамическая модель узла трения». Под динамической моделью понимают описание механизма (узла трения), отражающее его динамические свойства и связи с помощью совокупности символов, условных обозначений и аналитических приемов с условием, что динамические воздействия на модель вызывают реакцию, идентичную реальной в узлах трения.

В качестве примера рассмотрим узел ползуна и его динамическую модель. Пусть колебания в направляющих ползуна возбуждает сила P(t), приложенная к подвижной части ползуна, как это показано на рис. 2.1. На рис. 2.1,а приведено упрощенное изображение ползуна, перемещающегося в плоских направляющих скольжения, как одного из характерных механизмов машин: 1 - ползун; 2 - направляющие; 3 - массивная станина; 4 - муфта.

На рис. 2.1,б приведена динамическая двухмассовая модель, описывающая нормальные колебания ползуна, где М₁ и М₂ - соответственно масса ползуна и станины; P(t) - возмущающаяся сила (например, создаваемая работой двигателя); К₁ и К₂ - контактная жесткость в соединениях (К₁ - жесткость направляющих, К₂ - жесткость между станиной и основанием); С₁ и С₂ - характеристики демпфирующей способности стыков.

Как известно, в теории колебаний наиболее распространено описание динамики движения масс уравнениями Лагранжа. Классическим примером такого описания является уравнение линейного осциллятора, представляющего собой одно-

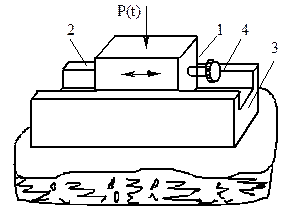
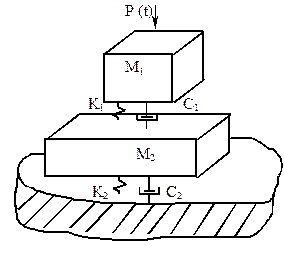
a б

Рис.2.1. Пример построения динамической модели узла трения:

а - схема механизма;

б - динамическая модель механизма

массовую модель механической системы (см. рис. 2.2), возбуждаемой гармонической силой P(t)=Psinwt и совершающей упругие колебания с амплитудой Х(t).

Колебания осциллятора m, вследствие суперпозиции сил при постоянных значениях К и С описываются уравнением колебаний:

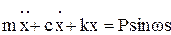, (2.1)

где m 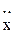- инерционная сила массы, пропорциональная ускорению 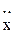; c 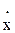- демпфирующая сила (неупругое сопротивление), пропорциональная скорости колебаний 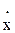; kх - упругая сила (пропорциональная перемещению х); P(t) - возмущающая сила, изменяющаяся по закону синуса.

Отметим, что динамические модели могут быть многомассовыми, но тогда возрастает сложность их математического описания.

В примере с ползуном можно учесть что станина не менее чем в 10 раз массивнее ползуна поэтому ее колебаниями по сравнению с колебаниями ползуна можно пренебречь.

Тогда, уравнение (2.1) позволит описать колебания ползуна m₁, а коэффициенты соответственно будут означать К - контактную жесткость стыка «ползун - станина», а c - коэффициент демпфирования в этом стыке.

Подобным образом моделируют узлы трения, а с целью упрощения описания производят приведение масс.

Например, кузов и раму автомобиля описывают единой массой, также описывают двигатель (большое число узлов трения), шасси и другие крупные компоненты транспортных средств.

В иных случаях, напротив, требуется детальное описание и расчет динамики узла. Например, топливный насос может быть описан как многомассовая система, в которой каждый плунжер может быть представлен отдельной массой.