Тема: Интегрирование четных и нечетных функций. Несобственные интегралы.
7.1. Интегрирование четных и нечетных функций.
Пусть 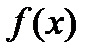 - четная функция на отрезке
- четная функция на отрезке  , т.е.
, т.е. 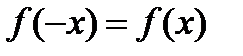 . Рассмотрим интеграл
. Рассмотрим интеграл
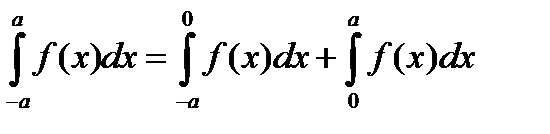
В интеграле 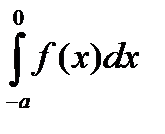 сделаем замену переменной
сделаем замену переменной 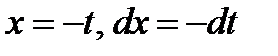 .
.
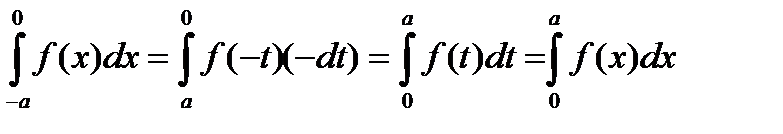
В результате получим
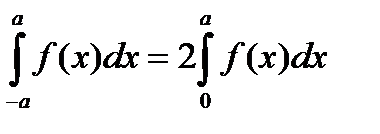
Пусть 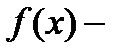 нечетная функция на отрезке
нечетная функция на отрезке 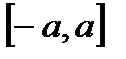 , т.е.
, т.е. 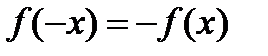 .
.
Как и в предыдущем случае в интеграле 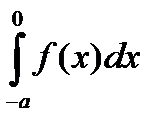 сделаем замену
сделаем замену 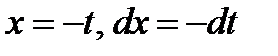 . В результате получим:
. В результате получим: 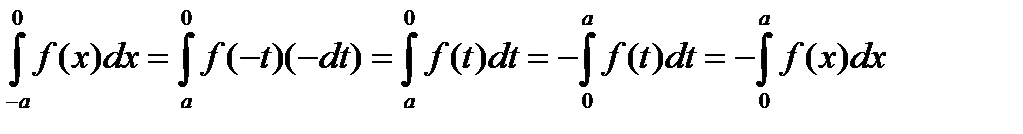 .
.
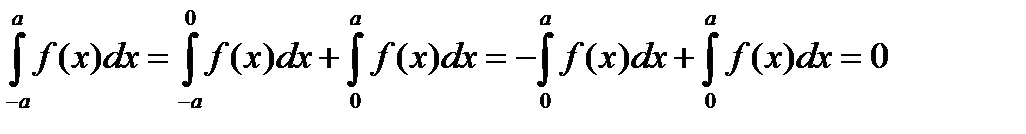 .
.
7.2. Несобственные интегралы.
До сих пор мы рассматривали интегралы 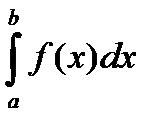 , для которых отрезок
, для которых отрезок 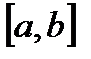 конечен и функция
конечен и функция 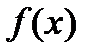 ограничена на отрезке
ограничена на отрезке 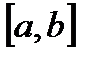 . При этом
. При этом 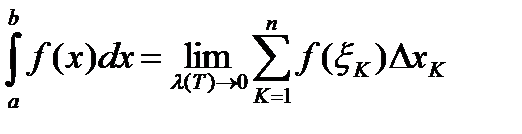 .
.
На практике часто встречаются случаи, когда 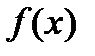 задана на бесконечном промежутке и непрерывна на нем либо
задана на бесконечном промежутке и непрерывна на нем либо 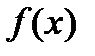 задана на конечном отрезке
задана на конечном отрезке 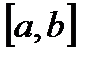 , но неограниченна на нем. Если промежуток
, но неограниченна на нем. Если промежуток 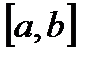 бесконечен, то при любом разбиении его на конечное число частей один из промежутков будет бесконечным, сумма
бесконечен, то при любом разбиении его на конечное число частей один из промежутков будет бесконечным, сумма 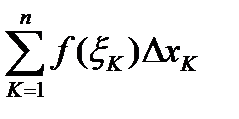 равна
равна  , а
, а 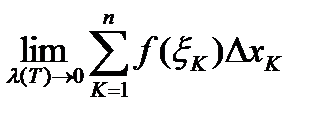 не существует. Если же
не существует. Если же 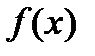 определена на конечном отрезке
определена на конечном отрезке 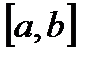 , но неограниченна, то всегда существует отрезок разбиения
, но неограниченна, то всегда существует отрезок разбиения 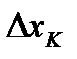 , на котором
, на котором 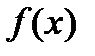 неограниченна и на этом отрезке можно выбрать точку
неограниченна и на этом отрезке можно выбрать точку 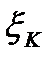 так, что
так, что  , где М наперед заданное число и в этом случае
, где М наперед заданное число и в этом случае 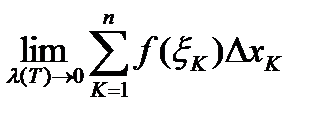 не существует.
не существует.
Если 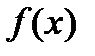 задана на бесконечном промежутке и непрерывна на нем либо
задана на бесконечном промежутке и непрерывна на нем либо 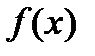 задана на конечном промежутке и неограниченна на нем, то интегралы от таких функций определяются с помощью предельного перехода и эти интегралы называются несобственными.
задана на конечном промежутке и неограниченна на нем, то интегралы от таких функций определяются с помощью предельного перехода и эти интегралы называются несобственными.
7.2.1. Несобственные интегралы от непрерывных функций по бесконечному промежутку.
Пусть 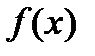 задана и непрерывна на промежутке
задана и непрерывна на промежутке 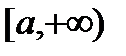 .
.
Рассмотрим интеграл 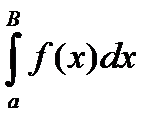 , этот интеграл существует
, этот интеграл существует 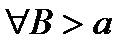 , т.к.
, т.к. 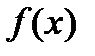 непрерывна на отрезке
непрерывна на отрезке 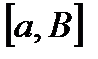 .
.
Положим по определению
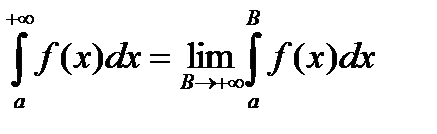 . (1)
. (1)
Интеграл 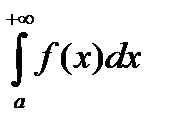 называется несобственным интегралом. Если предел в равенстве (1) существует, то говорят, что несобственный интеграл сходится. Если предел в равенстве (1) не существует, то говорят, что несобственный интеграл расходится.
называется несобственным интегралом. Если предел в равенстве (1) существует, то говорят, что несобственный интеграл сходится. Если предел в равенстве (1) не существует, то говорят, что несобственный интеграл расходится.
Пусть теперь функция 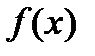 задана и непрерывна на промежутке
задана и непрерывна на промежутке 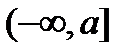 .
.
Несобственный интеграл 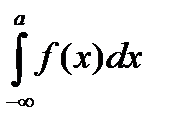 определяется аналогично:
определяется аналогично:
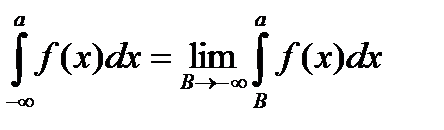
Далее, пусть функция 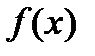 задана и непрерывна на всей числовой оси
задана и непрерывна на всей числовой оси 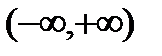 .
.
Несобственный интеграл 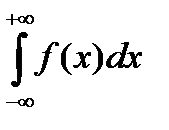 определяется следующим образом:
определяется следующим образом:
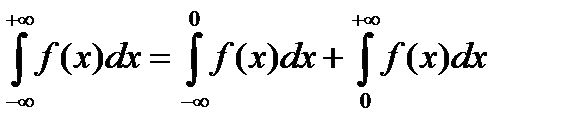 ,
,
при условии, что оба интеграла справа сходятся.
Заметим, что вместо 0 можно взять любое конечное число а и при этом сходимость несобственного интеграла 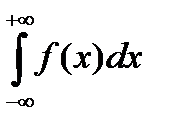 и его значение не изменится.
и его значение не изменится.
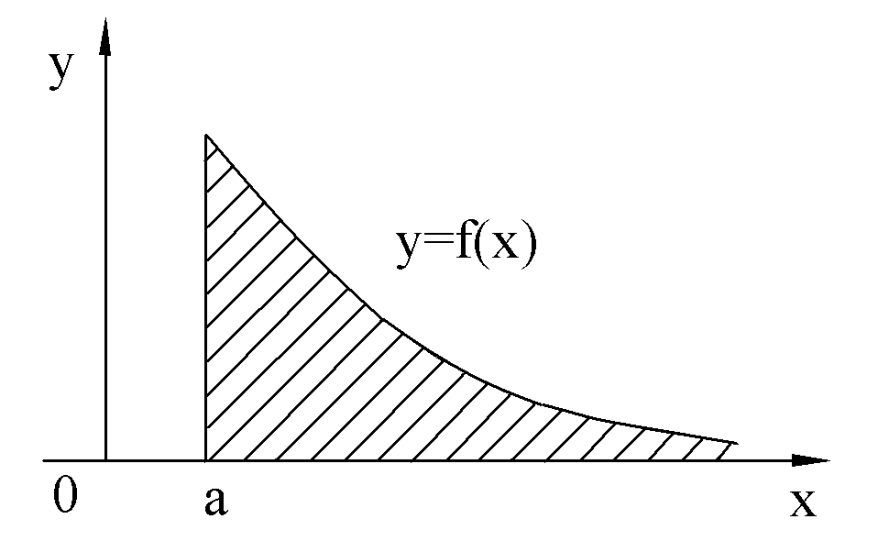
Геометрический смысл несобственного интеграла.
Если 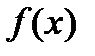 непрерывна и положительна в промежутке
непрерывна и положительна в промежутке 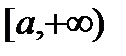 , то несобственный интеграл
, то несобственный интеграл  есть площадь бесконечной криволинейной трапеции, ограниченной осью ОХ, прямой
есть площадь бесконечной криволинейной трапеции, ограниченной осью ОХ, прямой 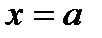 и графиком функции
и графиком функции 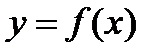 . Если несобственный интеграл
. Если несобственный интеграл 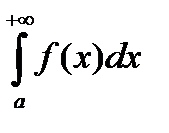 сходится, то соответствующая криволинейная трапеция имеет площадь равную несобственному интегралу
сходится, то соответствующая криволинейная трапеция имеет площадь равную несобственному интегралу 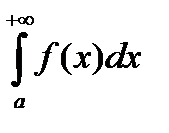 . Если же несобственный интеграл расходится, то криволинейная трапеция площади не имеет.
. Если же несобственный интеграл расходится, то криволинейная трапеция площади не имеет.
Механический смысл несобственного интеграла.
Если 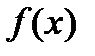 непрерывна и неотрицательна на промежутке
непрерывна и неотрицательна на промежутке 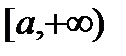 , то
, то 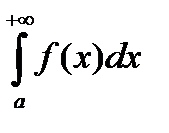 есть масса стержня
есть масса стержня 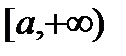 с плотностью
с плотностью 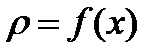 .
.
Пример. Вычислить 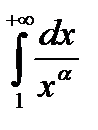
1) Пусть 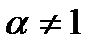 , тогда
, тогда 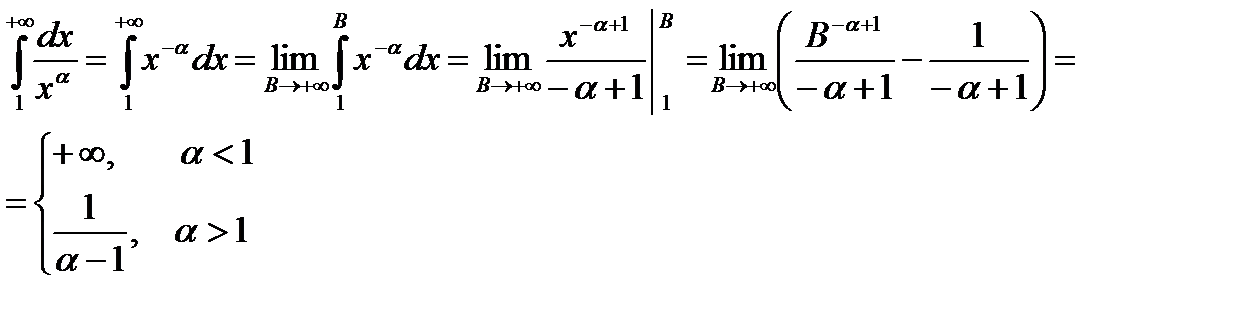
2) 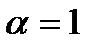 ;
; 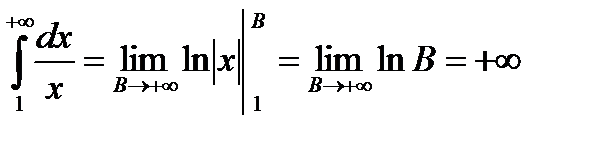 .
.
Следовательно, при 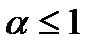 несобственный интеграл
несобственный интеграл 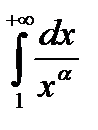 расходится, а при
расходится, а при 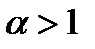 сходится.
сходится.
Пример. Вычислить интеграл 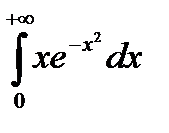 .
.
 .
.
Пример. Вычислить 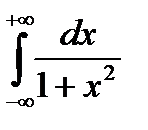
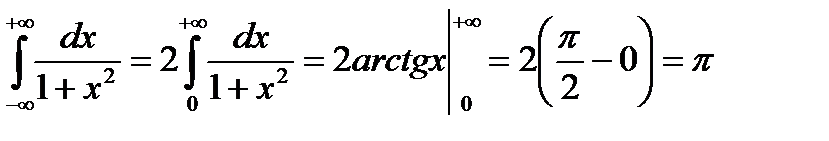
7.2.2. Несобственные интегралы от функций, заданных на конечном отрезке 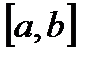 , но неограниченных на этом отрезке.
, но неограниченных на этом отрезке.
Пусть функция 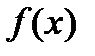 непрерывна в промежутке
непрерывна в промежутке 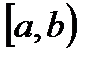 и неограниченна на этом промежутке.
и неограниченна на этом промежутке.
Рассмотрим произвольное 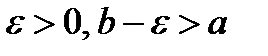 .
.
Интеграл 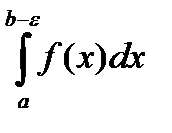 существует, т.к.
существует, т.к. 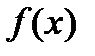 непрерывна на отрезке
непрерывна на отрезке 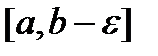 .
.
Несобственный интеграл 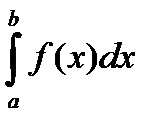 определяется следующим равенством
определяется следующим равенством
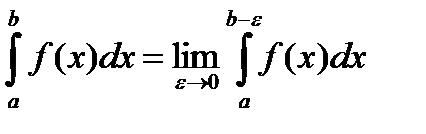 .
.
Если 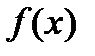 непрерывна в промежутке
непрерывна в промежутке 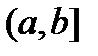 и неограниченна на нем, то несобственный интеграл
и неограниченна на нем, то несобственный интеграл 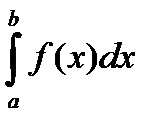 определяется аналогично предыдущему интегралу:
определяется аналогично предыдущему интегралу:
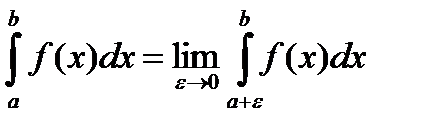 , где
, где 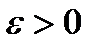 ;
; 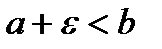 .
.
Пусть теперь 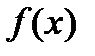 непрерывна на множестве
непрерывна на множестве 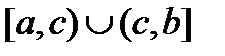 и неограниченна на этом множестве.
и неограниченна на этом множестве.
Несобственный интеграл 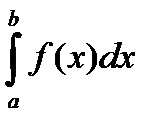 определяется следующим равенством:
определяется следующим равенством:
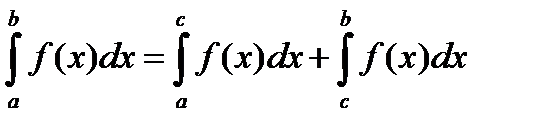 , если оба интеграла справа существуют.
, если оба интеграла справа существуют.
Далее рассмотрим случай, когда 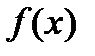 непрерывна в интервале
непрерывна в интервале 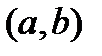 и неограниченна на этом интервале.
и неограниченна на этом интервале.
Несобственный интеграл 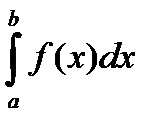 определяется равенством:
определяется равенством:
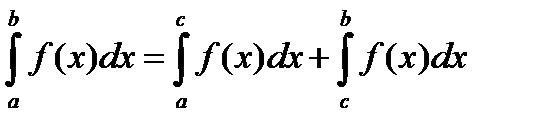 , где a<c<b, при этом оба интеграла в правой части должны существовать, т.е. должны сходиться.
, где a<c<b, при этом оба интеграла в правой части должны существовать, т.е. должны сходиться.
Можно показать, что сходимость интеграла 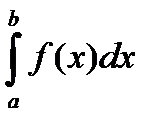 и его значение не зависят от выбора точки с.
и его значение не зависят от выбора точки с.
Пример. Вычислить интеграл 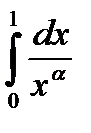 .
.
1) 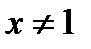
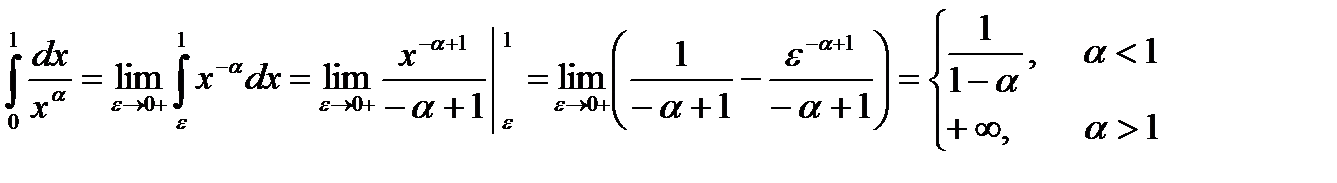
2) 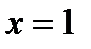
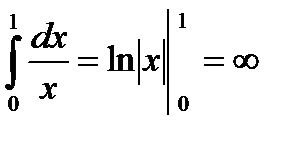 .
.
Таким образом, несобственный интеграл 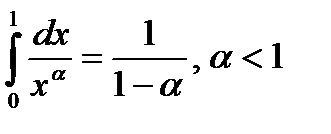 , сходится, а при
, сходится, а при 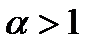 расходится.
расходится.
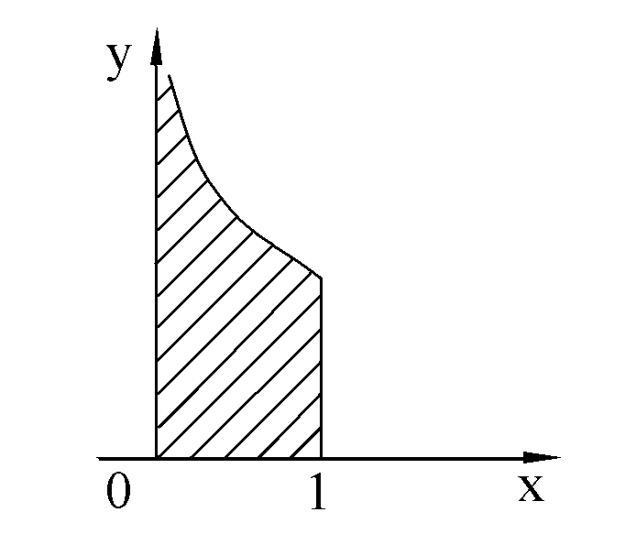
С геометрической точки зрения несобственный интеграл 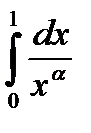 равен площади криволинейной трапеции, ограниченной осью OX, осью OY, прямой
равен площади криволинейной трапеции, ограниченной осью OX, осью OY, прямой 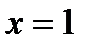 и графиком функции
и графиком функции 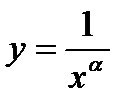 при
при 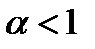 .
.
7.2.3. Признаки сходимости несобственных интегралов.
В данном пункте под несобственным интегралом 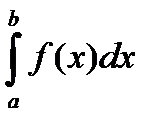 мы будем понимать какой-либо из ранее рассмотренных несобственных интегралов. В частности, a и b могут равняться
мы будем понимать какой-либо из ранее рассмотренных несобственных интегралов. В частности, a и b могут равняться 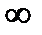 .
.
Теорема 1. Если в рассматриваемом промежутке выполняются неравенства 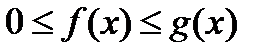 , то из сходимости несобственного интеграла
, то из сходимости несобственного интеграла 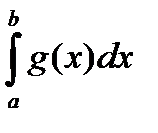 следует сходимость несобственного интеграла
следует сходимость несобственного интеграла 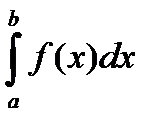 , а из расходимости интеграла
, а из расходимости интеграла 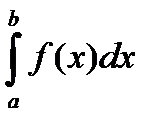 следует расходимость интеграла
следует расходимость интеграла 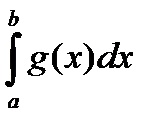 . (Без док-ва).
. (Без док-ва).
Определение. Несобственный интеграл 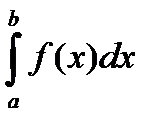 называется абсолютно сходящимся, если сходится интеграл
называется абсолютно сходящимся, если сходится интеграл 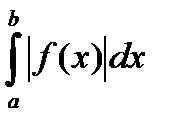 .
.
Теорема 2. Если несобственный интеграл 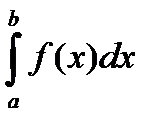 сходится абсолютно, то он сходится. (Без док-ва).
сходится абсолютно, то он сходится. (Без док-ва).
Пример. Исследовать на сходимость интеграл 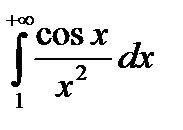 .
.
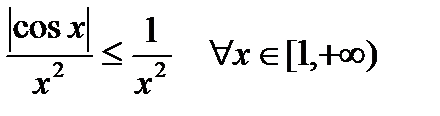
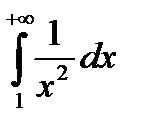 - сходится (см. п. 7.1.1.). По теореме 1 сходится интеграл
- сходится (см. п. 7.1.1.). По теореме 1 сходится интеграл 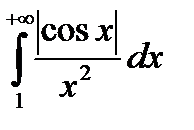 . Это означает, что данный интеграл сходится абсолютно. Следовательно, по теореме 2 данный интеграл сходится.
. Это означает, что данный интеграл сходится абсолютно. Следовательно, по теореме 2 данный интеграл сходится.
Отметим, что данные рассуждения не позволяют найти точное значение интеграла 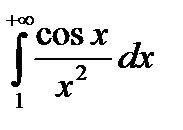 .
.
Дата добавления: 2015-08-21; просмотров: 3719;
