Тема: Интегрирование некоторых иррациональных выражений. Примеры интегралов, не выражающихся в элементарных функциях.
4.1. Вычисление интегралов вида: 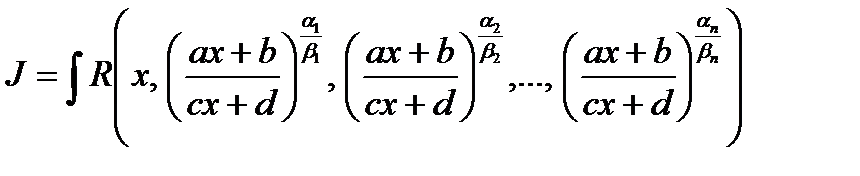 , где
, где 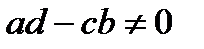 ,
, 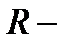 символ рациональности функции.
символ рациональности функции.
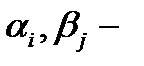 натуральные числа.
натуральные числа.
Пусть 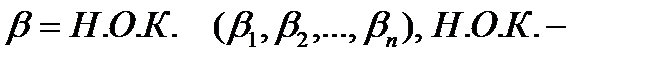 наименьшее общее кратное.
наименьшее общее кратное.
В данном интеграле сделаем замену
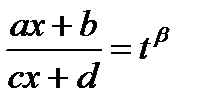 , тогда
, тогда 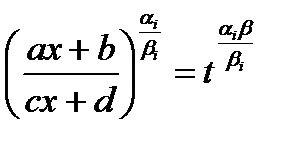 , где
, где 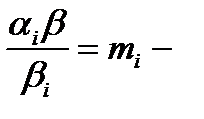 целое положительное число для любого
целое положительное число для любого 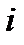 ,
, 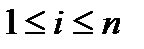 .
.
Далее имеем:
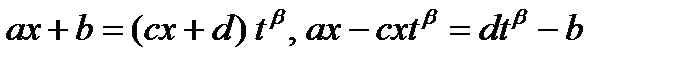
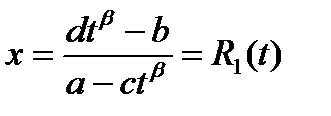 и
и 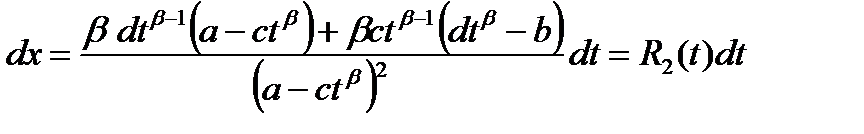
Сделав подстановку, получим:
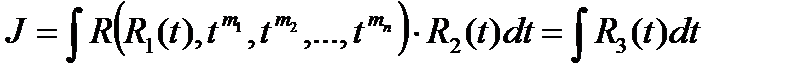
Таким образом, вычисление данного интеграла с помощью указанной замены сводится к вычислению интеграла от рациональной функции.
Пример. Вычислить интеграл 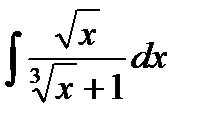 .
.
В данном интеграле сделаем замену: 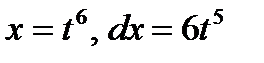
В результате замены получим:
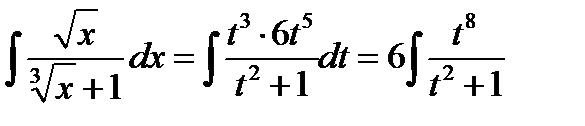
Неправильную рациональную дробь 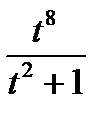 представим в виде суммы многочлена и правильной рациональной дроби, для этого поделим числитель на знаменатель:
представим в виде суммы многочлена и правильной рациональной дроби, для этого поделим числитель на знаменатель:
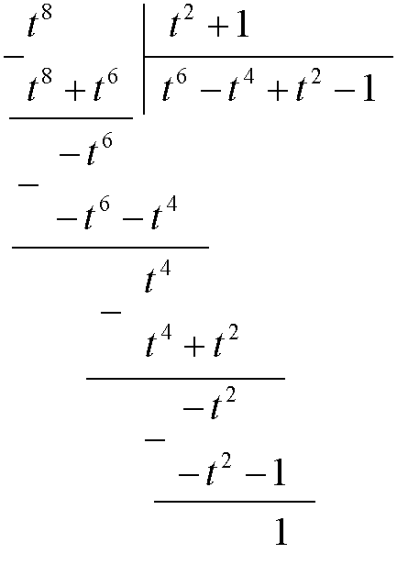
Таким образом, имеем:
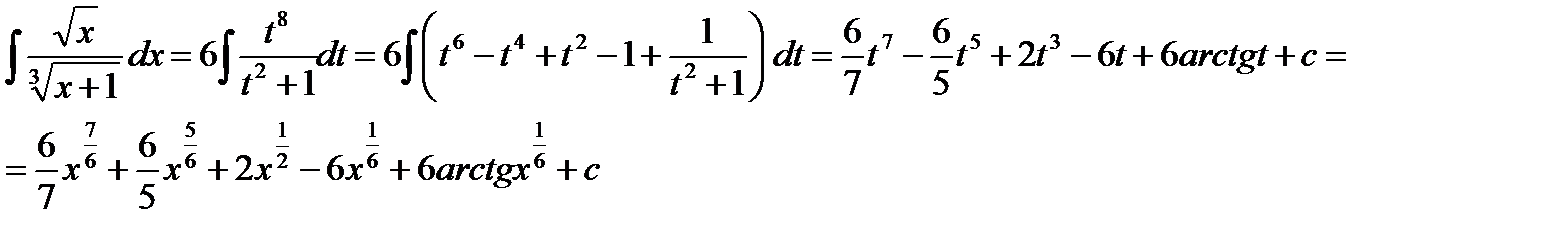
4.2. Вычисление интегралов вида:
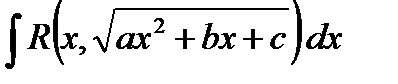
Выражение 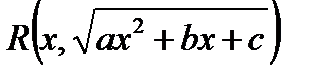 означает следующее: если
означает следующее: если 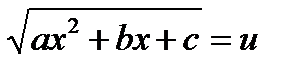 , то
, то 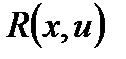 есть рациональная функция от
есть рациональная функция от 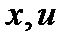 .
.
Интегрирование данных выражений можно осуществить различными способами.
4.2.1. Интеграл 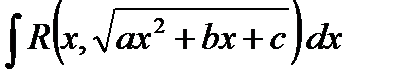 после выделения полного квадрата под знаком квадратного корня и замены
после выделения полного квадрата под знаком квадратного корня и замены 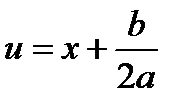 сводится к интегралу одного из следующего типов:
сводится к интегралу одного из следующего типов:
а) 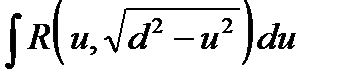
б) 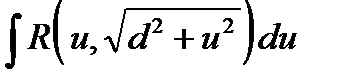
в) 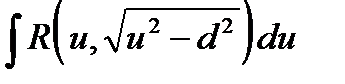
В свою очередь, последние три интеграла соответствующей подстановкой
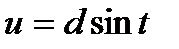
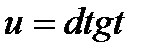
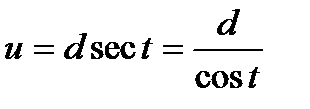
сводятся к интегралу вида:
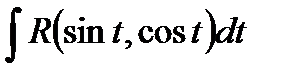
Пример. Вычислить: 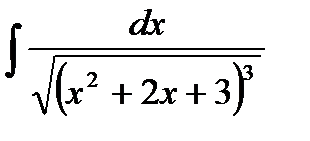
Выделяя полный квадрат в квадратном трехчлене x 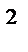 +2x+3, получим:
+2x+3, получим:
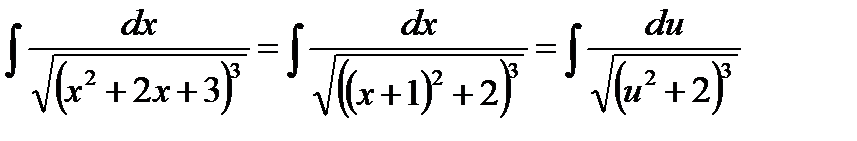 , где
, где 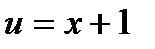 ,
, 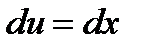
Делая подстановку 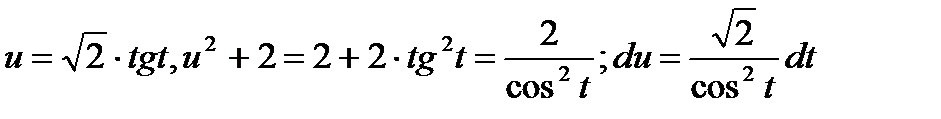 , получим:
, получим:
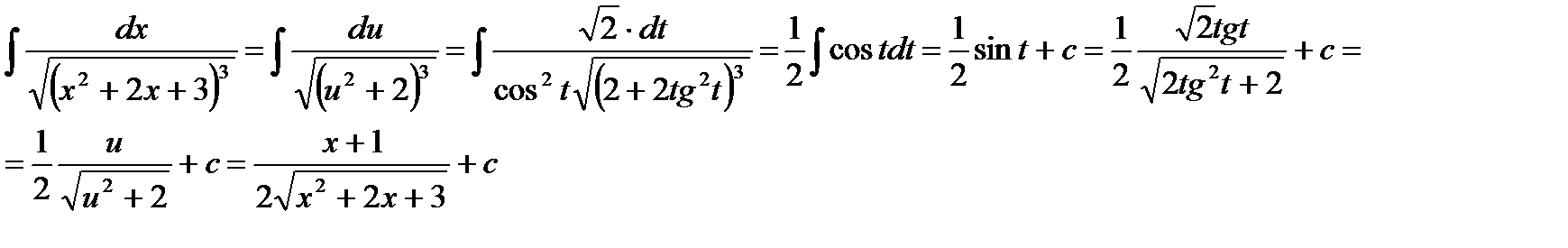
Пример. Вычислить: 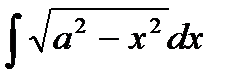
Делая подстановку 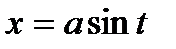 ,
, 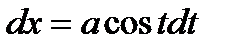 ,
, 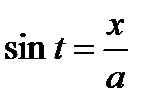 ,
, 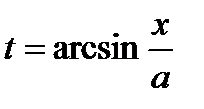 получим:
получим:
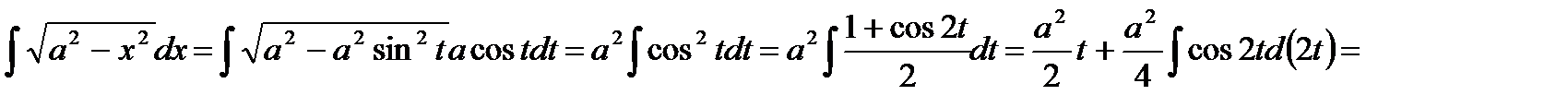
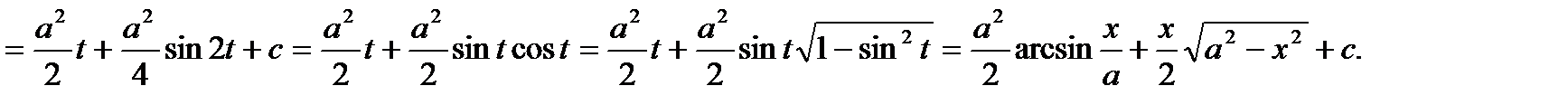
4.2.2. Подстановка Эйлера.
Интеграл 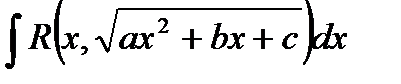 ,
, 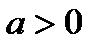 , может быть сведен к вычислению интеграла от рациональной функции с помощью подстановки
, может быть сведен к вычислению интеграла от рациональной функции с помощью подстановки 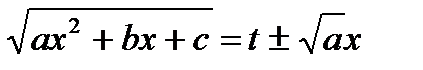 , которая носит имя Эйлера, впервые применившего эту подстановку.
, которая носит имя Эйлера, впервые применившего эту подстановку.
Пусть для определенности:
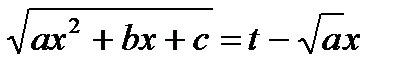
Возведем обе части последнего равенства в квадрат, в результате получим:
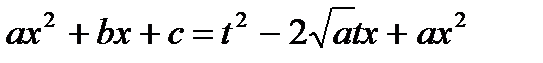
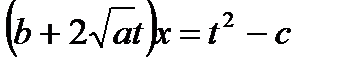 ;
; 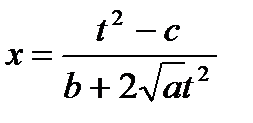 ;
;
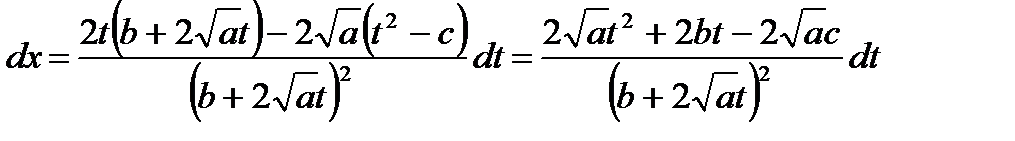
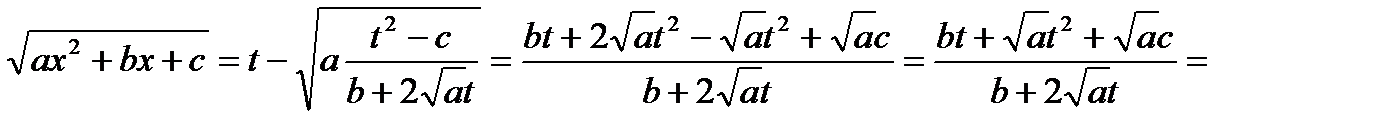
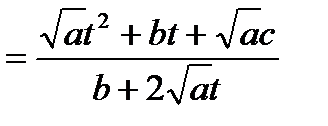 .
.
Используя данную подстановку, будем иметь:
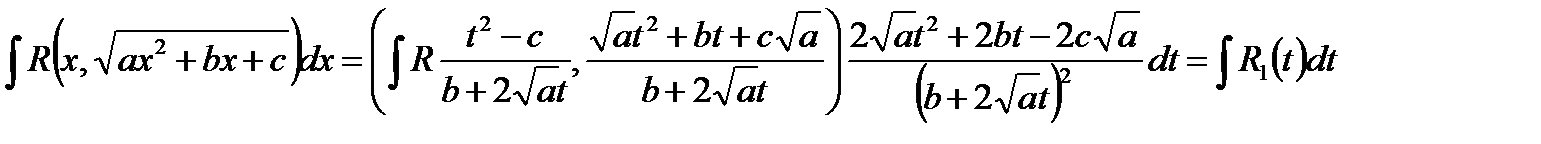 ,
,
т.к. рациональная функция от рациональной функции есть рациональная функция и произведение двух рациональных функций есть рациональная функция.
Пример. Вычислить: 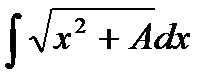
При вычислении данного интеграла используем подстановку Эйлера, т.к. коэффициент при x 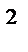 больше 0.
больше 0.
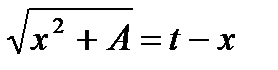 ;
; 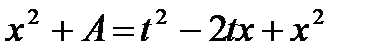 ;
; 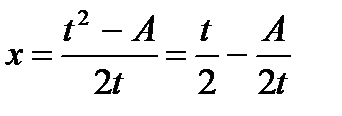 ;
;
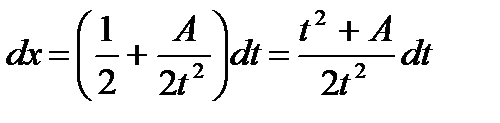 ;
; 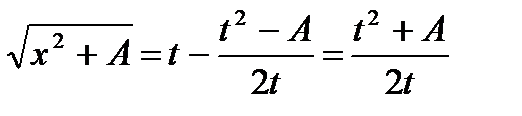 ;
;
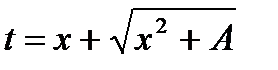 .
.
Осуществляя подстановку, получим:
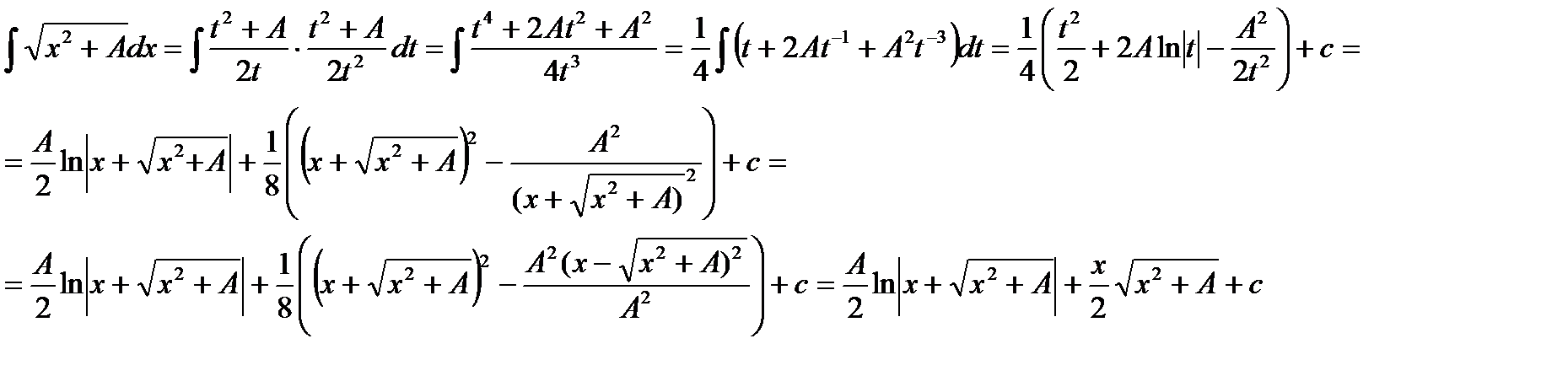
Пример. Вычислить: 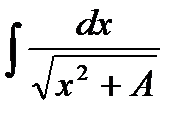
Применим снова подстановку Эйлера:
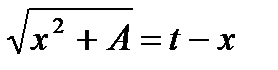 ,
, 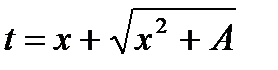
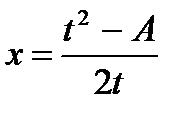
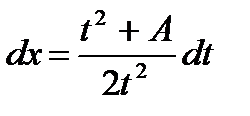
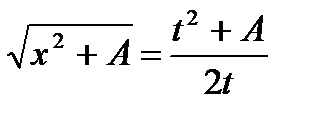 (см. пример 25)
(см. пример 25)
Далее имеем:
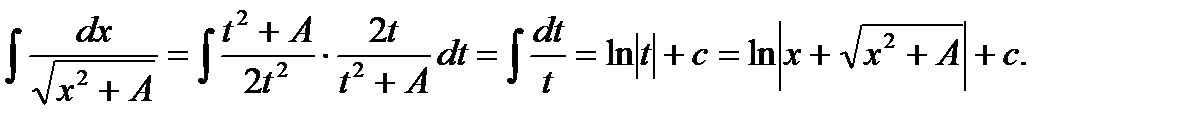
4.3. Примеры интегралов, не выражающихся в элементарных функциях:
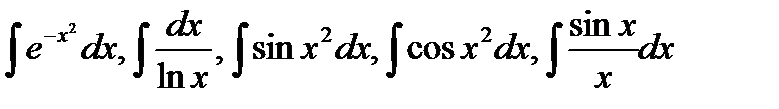 .
.
Дата добавления: 2015-08-21; просмотров: 1874;
